Isometría
Una isometría es una transformación geométrica que preserva la distancia entre cualquier par de puntos.
Es decir, si dos puntos están separados por cierta distancia antes de aplicar la transformación, esa distancia permanece exactamente igual después.
Por lo tanto, una isometría transforma cualquier figura en otra figura congruente.
En consecuencia, las isometrías también conservan la equivalencia de superficie.
Ejemplo
Consideremos un triángulo que se rota 90° en sentido horario y luego se traslada hacia la derecha. Las distancias entre los puntos A, B y C se mantienen inalteradas durante toda la transformación.
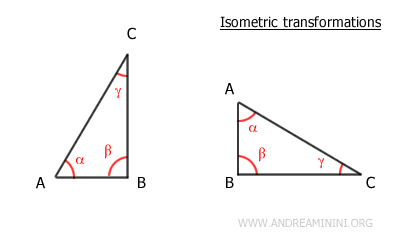
Tanto la rotación como la traslación son transformaciones isométricas.
El triángulo original y su imagen son congruentes, ya que sus lados correspondientes tienen la misma longitud. En consecuencia, también poseen la misma área.
El término "isométrico" suele emplearse como sinónimo de "congruente". Proviene del griego: "isos" significa "igual" y "metron" significa "medida". Por ejemplo, los dos triángulos mencionados son congruentes porque sus lados y ángulos se conservan idénticos tras la rotación o la traslación.
Las transformaciones que producen una isometría se denominan transformaciones isométricas o también transformaciones rígidas (o movimientos rígidos), ya que no alteran la forma ni el tamaño de las figuras.
Las figuras que permanecen invariantes bajo una isometría se llaman figuras isométricas, puesto que conservan sus medidas originales.
Tipos de Isometrías
Las principales transformaciones isométricas son:
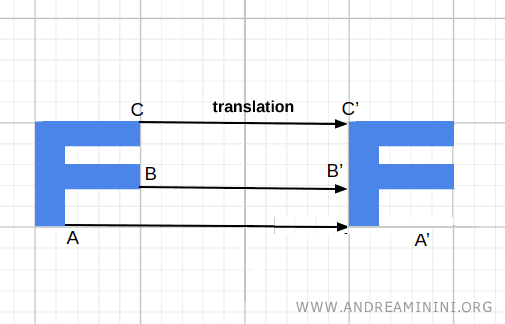
- Traslación
Cada punto de la figura se desplaza una distancia fija en una dirección determinada.
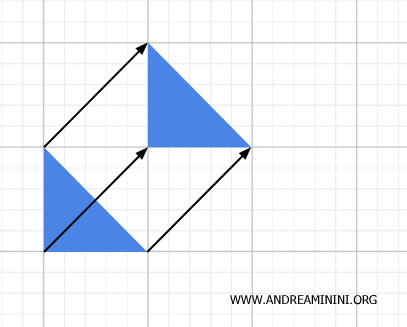
- Rotación
Cada punto gira alrededor de un punto fijo, llamado centro de rotación.
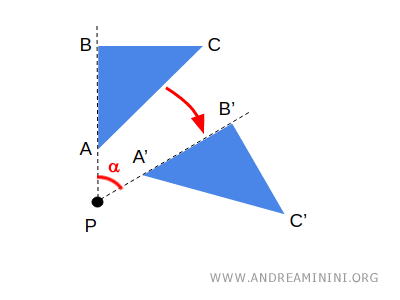
- Reflexión
Cada punto se refleja con respecto a una recta, conocida como eje de simetría.
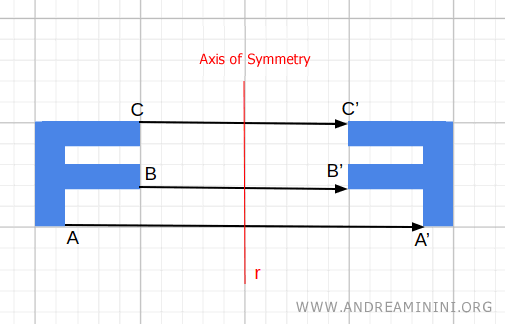
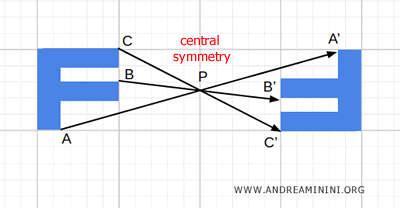
- Simetría central
Cada punto se transforma en su opuesto respecto a un punto central.
Composición de Isometrías
Cuando se aplican dos o más transformaciones isométricas de forma sucesiva sobre una figura, el resultado se denomina composición de isometrías.
Por ejemplo, podemos trasladar un triángulo 10 cm en dirección horizontal (traslación) y luego rotarlo 180° (rotación).

Es fundamental entender que la composición de dos isometrías sigue siendo una isometría.
Dado que cada transformación preserva distancias y formas, su composición también mantiene estas propiedades invariantes.
En otras palabras, una figura sometida a una composición de isometrías conserva su forma y dimensiones originales.
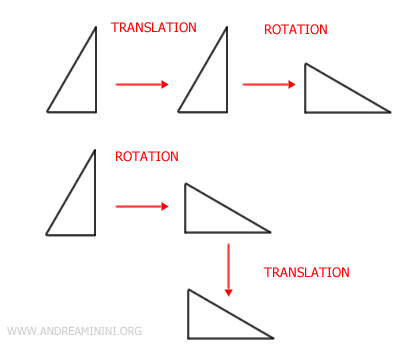
Nota: No obstante, la composición de isometrías no siempre es conmutativa. Es decir, el orden en que se aplican las transformaciones puede alterar el resultado final. Por ejemplo, rotar una figura y luego trasladarla no equivale, en general, a trasladarla y luego rotarla.
Algunas composiciones de isometrías reciben nombres específicos según las transformaciones que las integran. Por ejemplo:
- Reflexión deslizante
Es la combinación de una reflexión y una traslación, en la que la figura se refleja y luego se desplaza a lo largo del eje. - Rototraslación
Es la combinación de una rotación seguida de una traslación.
Isometrías Directas e Indirectas
Las isometrías se clasifican en directas o indirectas.
- Isometrías directas
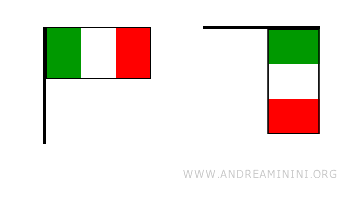
Son aquellas que conservan la orientación de la figura. Es decir, si una figura está orientada en sentido horario o antihorario, esa orientación se mantiene tras la transformación. Las traslaciones y rotaciones son ejemplos de isometrías directas. Por ejemplo, estas dos banderas pueden superponerse mediante una rotación seguida de una traslación. Esto constituye una isometría directa.
- Isometrías indirectas
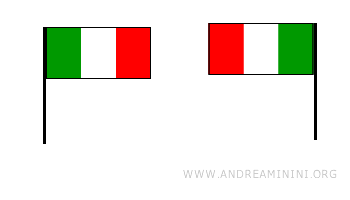
Son aquellas que invierten la orientación de la figura. Un caso típico es la reflexión axial, que cambia el sentido de giro (de horario a antihorario o viceversa). Por ejemplo, estas banderas solo pueden coincidir perfectamente tras una reflexión. Se trata, por tanto, de una isometría indirecta.
Nota: Un error habitual consiste en pensar que toda isometría indirecta requiere al menos dos transformaciones rígidas, cuando en realidad una única reflexión basta para invertir la orientación. Lo que determina si una isometría es directa o indirecta no es el número de pasos, sino el efecto final sobre la orientación de la figura.
Invariantes en una Isometría
En una isometría, algunos aspectos de la figura, como su posición, pueden cambiar, pero otros se mantienen constantes.
Las propiedades que permanecen inalteradas se denominan invariantes de la isometría.

Las principales propiedades invariantes bajo una isometría son:
- Distancia entre puntos
Las distancias entre puntos no varían. Por ejemplo, si la distancia entre A y B es de 5 cm, se mantendrá igual tras la transformación. - Longitud de los segmentos
Los lados de la figura conservan su longitud original. Por ejemplo, los segmentos AB, BC y AC mantienen la misma medida en ambos triángulos. - Medida de los ángulos
Los ángulos no se alteran. Así, los ángulos α, β y γ del triángulo siguen teniendo la misma amplitud tras la isometría. - Área de la figura
El área total no se modifica. El triángulo, por ejemplo, conserva su área tras la transformación. - Forma y tamaño
La figura conserva su forma y dimensiones, lo que garantiza su congruencia con la original. - Alineación de puntos
Si varios puntos están alineados en la figura original, seguirán alineados en la imagen resultante. - Paralelismo
Las rectas paralelas en la figura original siguen siéndolo en la transformada. - Perpendicularidad
Las rectas perpendiculares mantienen dicha relación. Por ejemplo, los segmentos AB y BC son perpendiculares tanto en el triángulo original como en su imagen.
Isometrías en el Espacio
Las isometrías en el espacio son transformaciones que conservan las distancias entre puntos correspondientes, manteniendo inalteradas la forma y el tamaño de los cuerpos geométricos, y modificando únicamente su posición y/o orientación.
En geometría bidimensional, las transformaciones isométricas incluyen traslaciones, rotaciones y reflexiones; lo mismo ocurre en el espacio tridimensional.
Las isometrías espaciales presentan las mismas propiedades fundamentales que en el plano:
- Conservan las distancias entre los puntos correspondientes.
- Transforman cada segmento en otro segmento congruente, de igual longitud.
- Mantienen los ángulos entre segmentos y también los ángulos entre planos.
Se dice que dos cuerpos son congruentes si comparten las siguientes características: aristas correspondientes de la misma longitud, ángulos congruentes, caras y aristas equivalentes, y ángulos diedros iguales.
- Sólidos directamente congruentes
Dos cuerpos son directamente congruentes si pueden superponerse exactamente mediante movimientos rígidos como traslaciones y rotaciones, sin necesidad de aplicar una reflexión.Ejemplo: Dos cubos idénticos que se pueden hacer coincidir mediante una combinación de traslaciones y rotaciones.
- Sólidos inversamente congruentes
Dos cuerpos son inversamente congruentes si solo pueden coincidir mediante una reflexión.Ejemplo: Un zapato derecho y uno izquierdo. Tienen la misma forma pero son imágenes especulares, por lo que solo pueden coincidir mediante una reflexión.
Isometrías en Geometría Analítica
En geometría analítica, toda isometría del plano - ya se trate de traslaciones, rotaciones, simetrías centrales, reflexiones o deslizamientos - puede describirse mediante una transformación afín de la forma
$$ \begin{cases} x' = ax + by + c \\ y' = a'x + b'y + c' \end{cases} $$
La matriz $\begin{pmatrix} a & b \\ a' & b' \end{pmatrix}$ constituye la parte lineal de la transformación, mientras que el vector $(c, c')$ representa la posible traslación.
De este modo, cualquier isometría del plano se expresa a través de ecuaciones lineales de primer grado en $x$ e $y$.
La matriz de coeficientes lineales es siempre una matriz ortogonal, lo que equivale a cumplir
$$ \begin{pmatrix} a & b \\ a' & b' \end{pmatrix}^{T} \begin{pmatrix} a & b \\ a' & b' \end{pmatrix} = I \, . $$
Además, el determinante de la matriz lineal de una isometría es siempre $\pm 1$:
$$ \det \begin{pmatrix} a & b \\ a' & b' \end{pmatrix} = ab' - a'b = \pm 1 . $$
En consecuencia, las isometrías del plano se clasifican en dos grandes tipos:
- Isometrías directas
Cuando el determinante es $+1$, la orientación se conserva. En este grupo se encuentran las traslaciones, las rotaciones y las simetrías centrales. - Isometrías opuestas
Si el determinante es $-1$, la transformación invierte la orientación. A esta clase pertenecen las reflexiones y los deslizamientos.
En todos los casos, la estructura analítica es análoga: una parte lineal ortogonal, eventualmente combinada con un vector de traslación.
Ejemplo 1
Una rotación de $90^\circ$ en sentido antihorario en el plano cartesiano se describe por
$$ \begin{cases} x' = -y \\ y' = x \end{cases} $$
Su matriz lineal es
$$ A = \begin{pmatrix} 0 & -1 \\ 1 & 0 \end{pmatrix}, \quad \det(A) = 0 \cdot 0 - (-1)\cdot 1 = +1 . $$
Como el determinante resulta positivo, esta transformación es una isometría directa.
Por ejemplo, al aplicar la rotación al punto $P(2,1)$ se obtiene $$ P(2,1) \;\;\longrightarrow\;\; P'(x',y') = (-1,2). $$
Ejemplo 2
La reflexión respecto al eje $y$ se expresa de la siguiente manera:
$$ \begin{cases} x' = -x \\ y' = y \end{cases} $$
La matriz lineal asociada es
$$ A = \begin{pmatrix} -1 & 0 \\ 0 & 1 \end{pmatrix}, \quad \det(A) = (-1)\cdot 1 - 0 = -1 . $$
El determinante negativo indica que se trata de una isometría opuesta.
Por ejemplo, al reflejar el punto $Q(3,2)$ obtenemos $$ Q(3,2) \;\;\longrightarrow\;\; Q'(-3,2). $$
Observaciones Adicionales
A continuación se presentan algunas observaciones y notas relevantes sobre las isometrías:
- Las isometrías son congruencias
Las isometrías son transformaciones geométricas que generan figuras congruentes, ya que preservan tanto la longitud de los segmentos como la medida de los ángulos. Como resultado, las figuras transformadas pueden superponerse punto por punto sobre las originales mediante movimientos rígidos, cumpliendo con la definición de congruencia en la geometría euclídea. - Las isometrías son un caso particular de semejanza
Las isometrías constituyen un tipo específico de semejanza, en la que la razón de semejanza es igual a 1. Cumplen con todas las propiedades propias de las semejanzas:- preservan el paralelismo entre segmentos,
- los ángulos correspondientes permanecen congruentes, y
- los segmentos correspondientes conservan la misma longitud.
- Identificación de las isometrías mediante los puntos fijos
La naturaleza de una isometría puede reconocerse analizando sus puntos fijos.- Un único punto fijo
Esta situación solo se da en los casos de rotación o de simetría central. En tales transformaciones, el punto fijo corresponde, respectivamente, al centro de rotación o al centro de simetría.

- Todos los puntos fijos
Cuando todos los puntos permanecen inmóviles, la transformación es una reflexión. En este caso, el eje de simetría es una recta formada por puntos invariantes, que no cambian de posición.

- Ningún punto fijo
La ausencia de puntos fijos es característica de las traslaciones y de las reflexiones deslizantes, ya que en estos movimientos ningún punto queda en reposo.
- Un único punto fijo
- El grupo de isometrías
El conjunto de todas las isometrías, con la operación de composición, constituye un grupo, ya que la composición es asociativa, existe una transformación identidad y cada isometría posee un inverso.
Y así sucesivamente.