Congruencia en geometría
Dos figuras geométricas se consideran congruentes si pueden coincidir punto por punto mediante un movimiento rígido.
Un movimiento rígido es aquel que desplaza la figura sin deformarla, mediante traslaciones, rotaciones y/o simetrías.
Por tanto, dos figuras congruentes tienen la misma forma y tamaño, aunque ocupan posiciones distintas en el espacio.
La congruencia se representa con el símbolo de “igual aproximadamente”, es decir, un signo igual con una tilde encima: ≅
$$ A ≅ B $$
El concepto de congruencia es esencial para identificar y comparar figuras geométricas.
Nota: La congruencia se introduce en el marco de la geometría euclidiana y se basa en transformaciones rígidas - o isometrías - como traslaciones, rotaciones y simetrías. Estas transformaciones modifican la posición de la figura en el espacio, pero no su forma ni su tamaño. Por tanto, si una figura puede transformarse en otra mediante una combinación de isometrías, son congruentes.
Ejemplo práctico
Consideremos dos copias de un mismo triángulo:
una de ellas está invertida respecto a la otra.
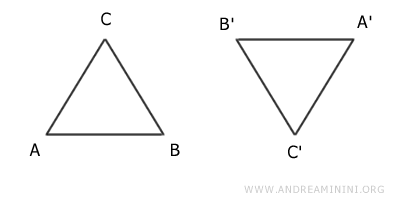
Estos dos triángulos no son idénticos, ya que, aunque tienen la misma forma y tamaño, no ocupan la misma posición en el espacio.
Sin embargo, sí son congruentes, pues pueden superponerse tras aplicar una rotación y una traslación.
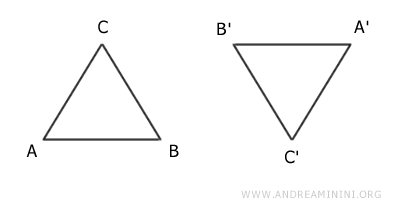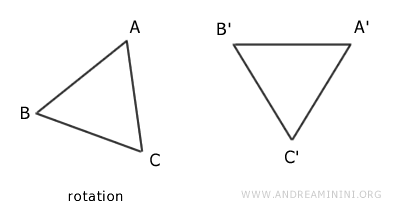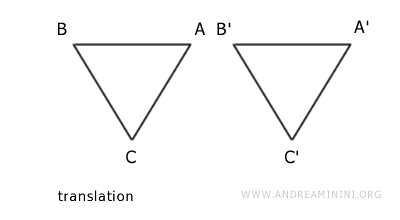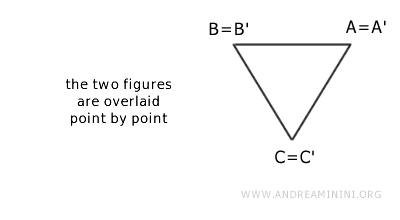
Una vez superpuestas, las dos figuras coinciden completamente.
Otros ejemplos de congruencia
En geometría plana:
- Dos segmentos son congruentes si tienen la misma longitud. Por ejemplo: AB ≅ CD
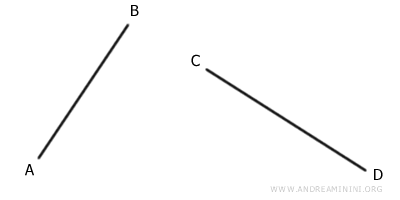
- Dos ángulos son congruentes si tienen la misma medida. Por ejemplo: α ≅ β
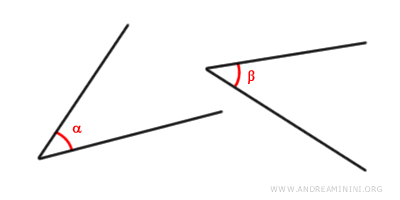
- Dos polígonos son congruentes si sus lados y ángulos correspondientes son congruentes.
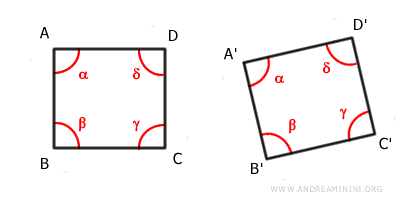
Nota: La congruencia de segmentos da lugar a algunos postulados importantes en geometría:
- Todas las rectas son congruentes entre sí.
- Todos los rayos son congruentes entre sí.
- Todos los semiplanos son congruentes entre sí.
En otras palabras, para establecer la congruencia entre dos figuras geométricas, es necesario que cumplan ciertos criterios.
Por ejemplo, dos triángulos son congruentes si verifican alguno de los siguientes criterios:
- Criterio Lado-Lado-Lado (LLL)
Dos triángulos son congruentes si sus tres lados son congruentes, es decir, de igual longitud. - Criterio Lado-Ángulo-Lado (LAL)
Dos triángulos son congruentes si tienen dos lados y el ángulo comprendido entre ellos congruentes. - Criterio Ángulo-Lado-Ángulo (ALA)
Dos triángulos son congruentes si tienen dos ángulos y el lado comprendido entre ellos congruentes.
Nota: Estos criterios son específicos para triángulos. Si dos triángulos cumplen uno de estos criterios, también cumplen los demás. Por tanto, basta con verificar uno de ellos para establecer su congruencia.
¿Cuál es la diferencia entre congruencia e igualdad?
Los términos "congruencia" e "igualdad" a menudo se emplean como sinónimos, aunque en geometría y matemáticas tienen significados distintos.
Dos figuras son iguales si coinciden punto por punto sin necesidad de aplicar ningún movimiento.
En otras palabras, dos figuras geométricas iguales ocupan la misma posición, con la misma forma y tamaño.
La igualdad se representa con el signo "=".
$$ A = B $$
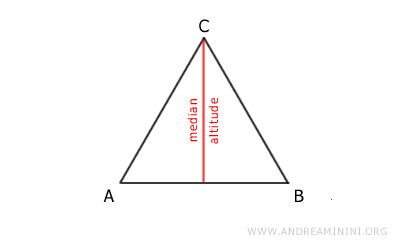
Por ejemplo, la altura y la mediana de un triángulo isósceles son iguales, ya que coinciden punto por punto.
En cambio, la congruencia requiere que las figuras puedan coincidir punto por punto después de aplicar un movimiento rígido.
Por tanto, dos figuras congruentes tienen la misma forma y tamaño, aunque ocupen posiciones distintas.
La congruencia se indica con el símbolo ≅:
$$ A ≅ B $$
Por ejemplo, los lados AB y BC de un triángulo isósceles son congruentes, ya que pueden superponerse tras una rotación y una traslación.

En resumen, la congruencia es un concepto más amplio que la igualdad, característico de la geometría, ya que permite que dos figuras con la misma forma y tamaño estén en posiciones distintas.
Diferencia entre congruencia y semejanza
La congruencia también se diferencia de la semejanza.
En la semejanza, las figuras geométricas tienen la misma forma, pero diferente tamaño.
Por ejemplo, estos dos triángulos no son congruentes, ya que no pueden superponerse.

No obstante, sí son semejantes, ya que ambos son triángulos isósceles con la misma forma, aunque de distinto tamaño.
El primer triángulo isósceles tiene lados más largos que el segundo.
Propiedades de la congruencia
Conviene destacar que la congruencia es una relación de equivalencia, pues cumple las propiedades de reflexividad, simetría y transitividad:
- Reflexividad
Toda figura es congruente consigo misma. - Simetría
Si la figura A es congruente con la figura B, entonces B es congruente con A. - Transitividad
Si la figura A es congruente con la figura B, y B es congruente con la figura C, entonces A es congruente con C.
Y así sucesivamente.