Planos
Un plano es un concepto fundamental en geometría, caracterizado por dos dimensiones: longitud y anchura.
Un plano se extiende de forma ilimitada en todas las direcciones y carece tanto de grosor como de límites.
Por convención, suele representarse mediante una letra del alfabeto griego (por ejemplo, α, β, γ, δ, etc.).
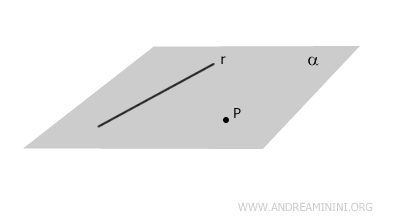
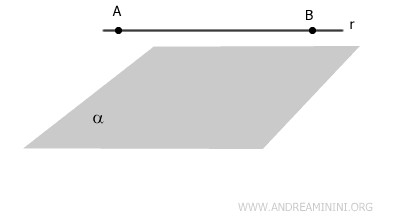
Cuando una recta o un punto se encuentran sobre un plano, se dice que pertenecen a él.
Por ejemplo, la recta r pertenece al plano alfa.
¿Cómo se Define un Plano?
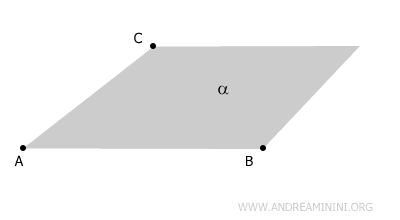
Un plano queda determinado por tres puntos no colineales (A, B, C), ya que por tres puntos que no estén alineados pasa un único plano α.
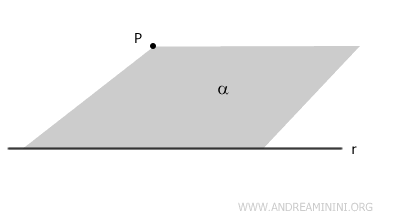
Otra manera de definir un plano es a partir de una recta y un punto que no se encuentre sobre ella.
Dada una recta r y un punto P exterior a ella, existe un único plano α que los contiene a ambos.
Por último, un plano también puede definirse mediante dos rectas que se intersecan.
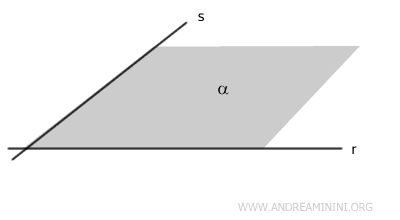
Por dos rectas secantes r y s pasa un único plano α.
Semi-Plano
Un semi-plano es una porción de un plano delimitada por una recta.
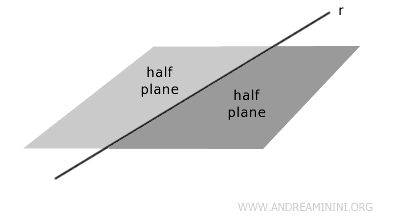
En otras palabras, cuando se traza una recta sobre un plano, esta lo divide en dos regiones distintas, cada una de las cuales constituye un semi-plano.
Planos Secantes y Paralelos
Según su disposición en el espacio, dos planos distintos pueden ser secantes o paralelos.
- Planos Secantes
Dos planos se denominan secantes si comparten exactamente una recta.
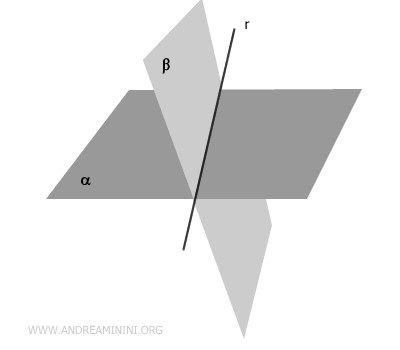
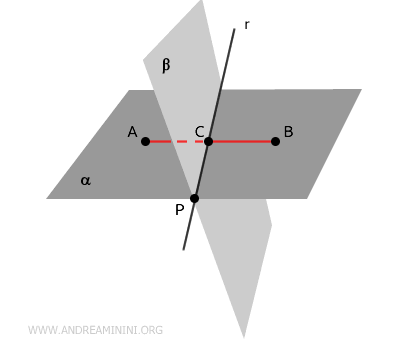
Teorema. Si dos planos distintos $ \alpha $ y $ \beta $ se intersectan en un punto $ P \in \alpha \cap \beta $, entonces comparten una recta común $ r $ que pasa por ese punto. $$ \exists \ r \ | \ P \in r, \ r \in \alpha \cap \beta $$
- Planos Paralelos
Dos planos son paralelos si no tienen ningún punto en común (planos paralelos distintos) o si coinciden en todos sus puntos (planos coincidentes).

La distancia entre dos planos paralelos es la longitud del segmento perpendicular a ambos planos que une un punto de cada uno.
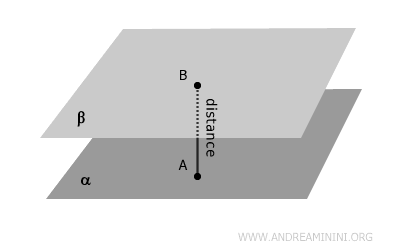
La relación de paralelismo entre planos posee propiedades reflexiva, simétrica y transitiva.
- Propiedad Reflexiva
Todo plano es paralelo a sí mismo. $$ \alpha || \alpha $$ - Propiedad Simétrica
Si el plano α es paralelo al plano β, entonces el plano β es paralelo al plano α. $$ \alpha || \beta \Leftrightarrow \beta || \alpha $$ - Propiedad Transitiva
Si el plano α es paralelo al plano β y el plano β es paralelo al plano γ, entonces el plano α es paralelo al plano γ. $$ \alpha || \beta \ , \ \beta || \gamma \Rightarrow \alpha || \gamma $$
Posición de una Recta Respecto a un Plano
Una recta puede situarse respecto a un plano en las siguientes posiciones:
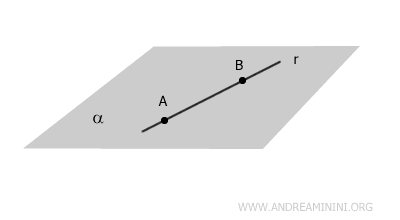
- Recta Coplanaria (o contenida en el plano)
La recta se encuentra sobre el plano. Todos sus puntos pertenecen a él, es decir, r⋂α=r.
- Recta Secante
La recta y el plano comparten exactamente un punto: r⋂α={P}. Una recta secante puede ser perpendicular u oblicua al plano.
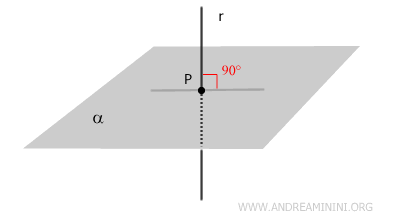
- Recta Perpendicular a un Plano
Si la recta es perpendicular a todas las rectas del plano que pasan por el punto de intersección (llamado pie de la perpendicular).
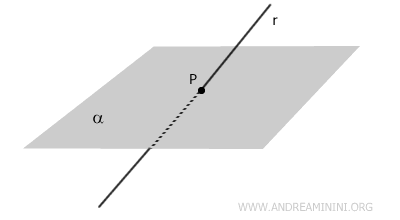
- Recta Oblicua
Si la recta no es perpendicular al plano.
- Recta Perpendicular a un Plano
- Recta Paralela a un Plano
La recta no tiene puntos en común con el plano: r⋂α=Ø.
Si una recta \( r \) es paralela a un plano \( \alpha \), cualquier otro plano \( \beta \) que contenga a \( r \) y no sea paralelo a \( \alpha \) lo cortará en una recta \( s \), la cual será paralela a \( r \).
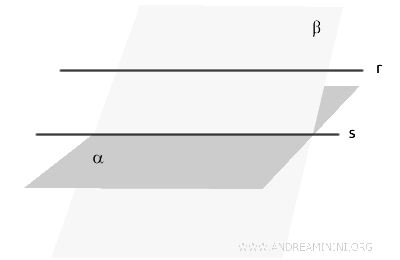
Esto ocurre porque las rectas \( r \) y \( s \), al ser coplanarias, se encuentran en el mismo plano \( \beta \) y nunca se intersectan.
Y así sucesivamente.