Haz de Planos
Un haz de planos es un conjunto infinito de planos definido por un parámetro real. Según el caso, los planos pueden compartir una misma recta de intersección o ser todos paralelos entre sí.
Haz Propio de Planos
Dada una recta \( r \), un haz propio de planos está constituido por todos los planos que contienen dicha recta. $$ \lambda_1 ( a_1x + b_1y + c_1z + d_1 ) + \lambda_2 ( a_2x + b_2y + c_2z + d_2 ) = 0 $$ $$ ( a_1x + b_1y + c_1z + d_1 ) + \frac{\lambda_2}{\lambda_1} ( a_2x + b_2y + c_2z + d_2 ) = 0 $$
Estas dos ecuaciones representan dos planos distintos.
La intersección de ambos es precisamente la recta \( r \).
$$ \begin{cases} \lambda_1 ( a_1x + b_1y + c_1z + d_1 ) \\ \lambda_2 ( a_2x + b_2y + c_2z + d_2 ) \end{cases} $$
Ejemplo
Supongamos que se nos da la ecuación de una recta en el espacio, definida como la intersección de dos planos:
$$ \begin{cases} 2x + 3y + 8z + 2 = 0 \\ -4x - 6y + 6z - 12 = 0 \end{cases} $$
El conjunto de puntos que satisface simultáneamente ambas ecuaciones constituye la recta.

En este caso, el haz propio de planos que pasa por la recta se expresa así:
$$ ( 2x + 3y + 8z + 2 ) + \frac{\lambda_2}{\lambda_1} ( -4x - 6y + 6z - 12 ) = 0 $$
donde \(\lambda_1\) y \(\lambda_2\) son escalares arbitrarios, con \(\lambda_2 \neq 0\).
Para simplificar, podemos definir \( k = \lambda_2 / \lambda_1 \), y la ecuación se reescribe de la siguiente manera:
$$ ( 2x + 3y + 8z + 2 ) + k ( -4x - 6y + 6z - 12 ) = 0 $$
Al variar \( k \), se obtienen todos los planos del haz que contienen la recta \( r \), es decir, todos los planos que “giran” alrededor de dicha recta.
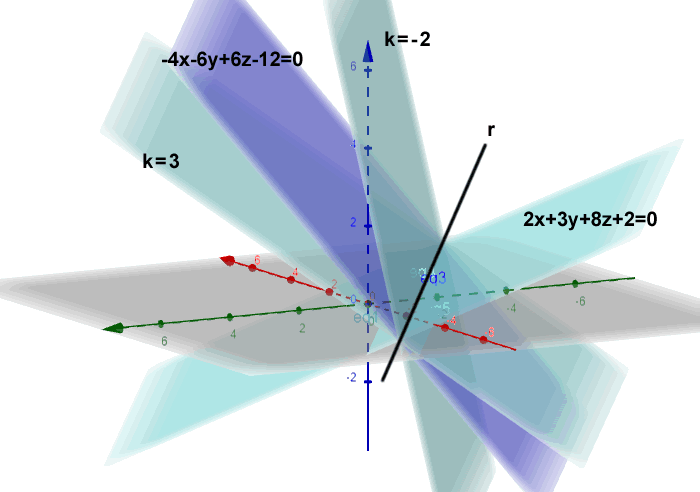
Este conjunto constituye el haz propio de planos asociado a la recta \( r \).
Haz Impropio de Planos
Dado un plano \( A \), un haz impropio de planos está formado por todos los planos paralelos a \( A \). $$ ax + by + cz + d = 0 $$
Para generar planos paralelos basta con modificar el término independiente \( d \).
Los coeficientes \( a, b, c \) no pueden ser todos nulos simultáneamente.
Ejemplo
Consideremos la ecuación de un plano en el espacio:
$$ 2x + 3y + 8z + 2 = 0 $$
Variando el término independiente \( k \), se obtiene la familia de planos paralelos al plano dado:
$$ 2x + 3y + 8z + k = 0 $$
Por ejemplo, para \( k = -12 \) y \( k = -25 \), la representación gráfica sería la siguiente:
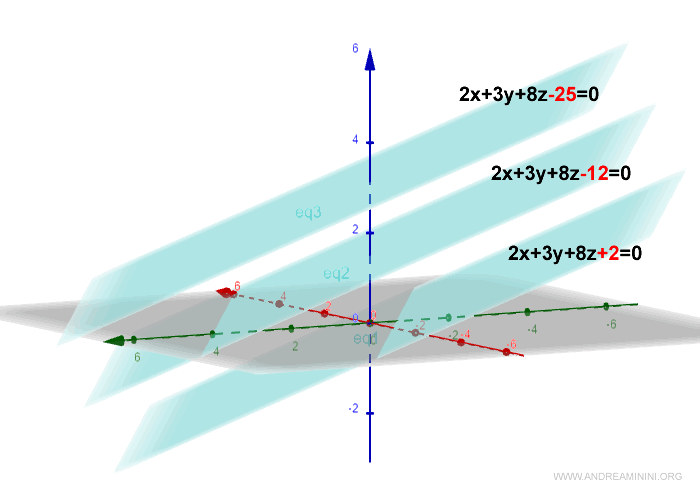
Y así sucesivamente.