Distancia de un Punto a un Plano

La distancia entre un punto P y un plano es la longitud del segmento perpendicular que une el punto P con el plano.

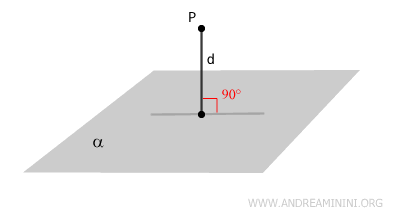
En otras palabras, la distancia de un punto P a un plano es la longitud del segmento de recta perpendicular trazado desde P hasta el plano.

Esta distancia siempre es un valor no negativo. Si el punto pertenece al plano, la distancia es cero.

Cálculo de la Distancia entre un Punto y un Plano

La distancia más corta entre un punto $ P(x_0, y_0, z_0) $ y un plano α de ecuación $ ax + by + cz + d = 0 $ en el espacio, corresponde a la longitud del segmento perpendicular que va de P al plano α.

$$ d(P, \alpha ) = \frac{|ax_0 + by_0 + cz_0 + d|}{\sqrt{a^2 + b^2 + c^2}} $$

Ejemplo

Consideremos el punto P con coordenadas (x; y; z) = (1; 3; 2) en el espacio tridimensional:

$$ P = \begin{pmatrix} 1 \\ 3 \\ 2 \end{pmatrix} $$

La ecuación cartesiana del plano es:

$$ 4x - 2y + z - 5 = 0 $$

Calculamos la distancia entre el punto y el plano utilizando la fórmula anterior.

$$ d(P, \alpha) = \frac{|ax_0 + by_0 + cz_0 + d|}{\sqrt{a^2 + b^2 + c^2}} $$

Los coeficientes de la ecuación del plano son: a = 4, b = -2, c = 1 y d = -5:

$$ d(P, \alpha) = \frac{|4 \cdot x_0 - 2 \cdot y_0 + 1 \cdot z_0 - 5|}{\sqrt{4^2 + (-2)^2 + 1^2}} $$

$$ d(P, \alpha) = \frac{|4 \cdot x_0 - 2 \cdot y_0 + z_0 - 5|}{\sqrt{21}} $$

Sustituyendo las coordenadas del punto: x₀ = 1, y₀ = 3, z₀ = 2:

$$ d(P, \alpha) = \frac{|4 \cdot 1 - 2 \cdot 3 + 1 \cdot 2 - 5|}{\sqrt{21}} $$

$$ d(P, \alpha) = \frac{|-5|}{\sqrt{21}} $$

$$ d(P, \alpha) = \frac{5}{\sqrt{21}} \approx 1.09 $$

Por lo tanto, la distancia entre el punto P y el plano es de aproximadamente 1.09.

En la siguiente imagen, esta distancia se representa mediante la línea roja que une el punto P con el plano.

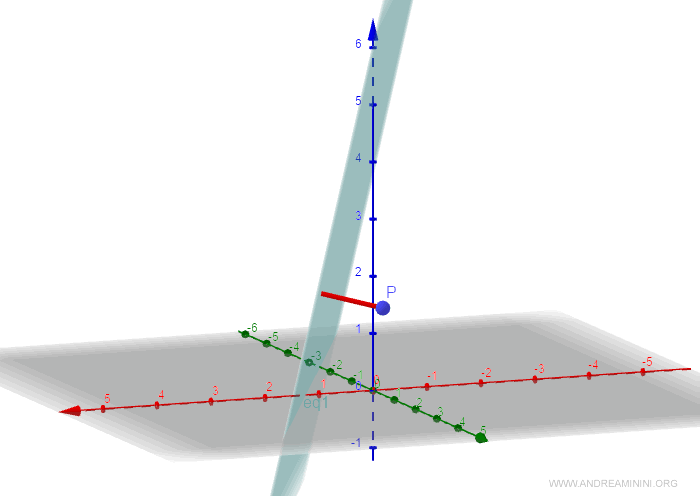
Se trata, en definitiva, de la longitud del segmento perpendicular que une el punto P con el plano.

Notas

Algunas observaciones adicionales sobre la distancia entre un punto y un plano:

• Teorema
  Dado un plano \( \alpha \) y un punto \( P \) exterior a él, el segmento perpendicular \( PH \) trazado desde \( P \) hasta el plano siempre es más corto que cualquier segmento oblicuo \( PQ \).
  

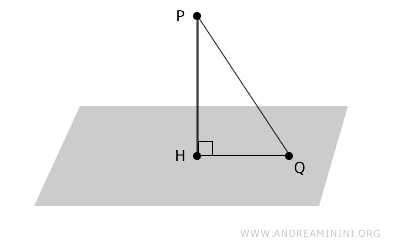
  Demostración. Sea \( PH \) el segmento perpendicular desde \( P \) al plano \( \alpha \), y \( PQ \) un segmento oblicuo cualquiera, siendo \( Q \) un punto sobre \( \alpha \). Los puntos P, H y Q forman un triángulo rectángulo \( PHQ \). Según el teorema de Pitágoras, el lado oblicuo siempre es mayor que cualquiera de los catetos, por lo que \( PQ > PH \). Por tanto, el segmento perpendicular \( PH \) es la distancia mínima entre \( P \) y el plano.

• Corolario
  Si desde un punto \( P \) se trazan dos segmentos oblicuos hacia un plano \( \alpha \) cuyas proyecciones sobre el plano son congruentes, entonces dichos segmentos también son congruentes, y viceversa. 
  

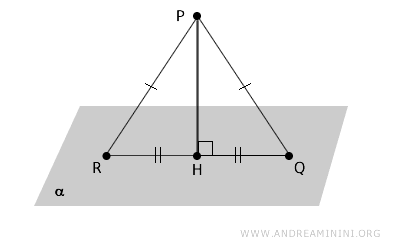
  Demostración. Consideremos dos segmentos oblicuos congruentes \( PQ \cong PR \) y el segmento perpendicular \( PH \) desde \( P \) al plano \( \alpha \). Por los criterios de congruencia de triángulos, los triángulos \( PHR \) y \( PHQ \) son congruentes, ya que comparten dos lados iguales y un ángulo congruente. En consecuencia, las proyecciones \( HR \cong HQ \) también son congruentes, lo cual implica que segmentos oblicuos congruentes \( PR \cong PQ \) tienen proyecciones congruentes sobre el plano \( \alpha \).

• Corolario
  Si desde un punto \( P \) se trazan dos segmentos oblicuos hacia un plano \( \alpha \) y sus proyecciones son de diferente longitud, el segmento cuya proyección es mayor también es más largo.
  

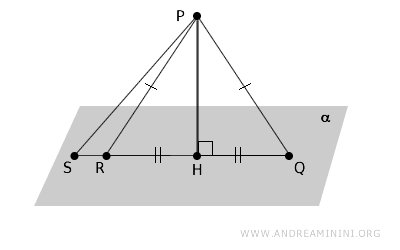
  Ejemplo. En este caso, el segmento oblicuo \( PS \) es más largo que \( PR \). Por tanto, su proyección \( HS \) también es mayor, es decir, \( HS > HR \).

Y así sucesivamente.