Ecuación de un Plano

La ecuación de un plano describe todos los puntos (x, y, z) que se encuentran sobre un determinado plano en el espacio tridimensional. Su forma general se expresa así: $$ ax + by + cz + d = 0 $$ donde $a$, $b$ y $c$ son las componentes de un vector normal al plano, y $d$ es una constante que determina la posición del plano respecto al origen.

Se trata de una de las ecuaciones fundamentales de la geometría analítica para representar superficies en el espacio 3D.

El plano está constituido por el conjunto infinito de puntos que cumplen esta ecuación general, también conocida como forma implícita.

$$ ax + by + cz + d = 0 $$

En función del contexto, la ecuación del plano puede escribirse también en forma explícita:

$$ z = mx + ny + q $$

Nota: El vector normal $\vec{n} = (a, b, c)$ es perpendicular al plano; es decir, forma un ángulo de 90° con cualquier dirección contenida en dicho plano.

Un Ejemplo Práctico

Consideremos la ecuación:

$$ 2x - 3y + 4z - 5 = 0 $$

Todo punto $(x, y, z)$ que satisface esta ecuación pertenece al plano.

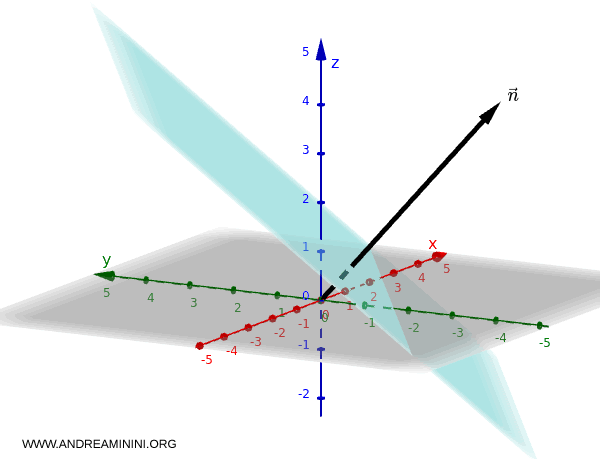
El vector normal a este plano es $\vec{n} = (2, -3, 4)$.

Cualquier vector contenido en el plano resulta ortogonal a este vector normal.

Ecuación del Plano en Forma Explícita

La forma explícita de la ecuación de un plano se escribe como $$ z = m x + n y + q $$

Cuando se representa un plano en el espacio tridimensional, es frecuente utilizar la forma general:

$a x + b y + c z + d = 0$

Aunque es una forma compacta, no siempre resulta la más intuitiva de interpretar.

Para hacerla más legible, puede despejarse la variable $z$, siempre que el coeficiente $c \ne 0$. En tal caso, la ecuación se reordena así:

$$ c z = -a x - b y - d $$

$$ z = - \frac{a}{c} x - \frac{b}{c} y - \frac{d}{c} $$

Resulta práctico introducir las siguientes sustituciones: $m = -\frac{a}{c}$,  $n = -\frac{b}{c}$,  $q = -\frac{d}{c}$

de modo que la ecuación adopta la forma:

$$ z = m x + n y + q $$

Esta es la denominada forma explícita de la ecuación de un plano.

¿Cuándo puede emplearse la forma explícita? Solo es posible reescribir la ecuación de un plano en forma explícita si el plano no es paralelo al eje $z$. Si $c = 0$, la ecuación se reduce a: $$ a x + b y + d = 0 $$ En este caso, la variable $z$ no aparece, lo que significa que el plano es paralelo al eje $z$ y, por tanto, no puede expresarse en forma $z = \dots$.

Ejemplo

Consideremos el plano definido por la ecuación:

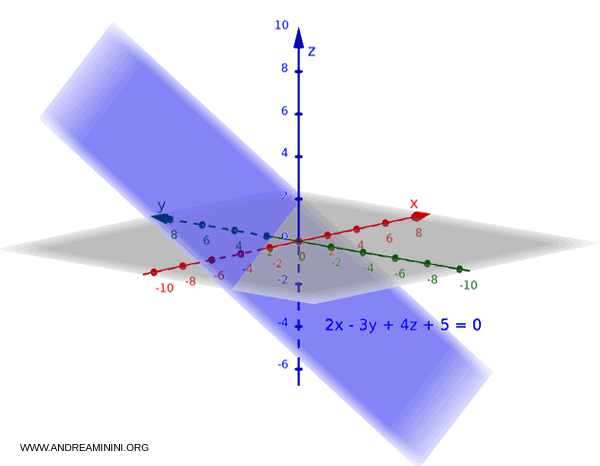
$$ 2x - 3y + 4z + 5 = 0 $$

Como $c = 4 \ne 0$, podemos expresarlo en forma explícita:

$$ z = -\frac{2}{4}x + \frac{3}{4}y - \frac{5}{4} $$

$$ z = -0.5x + 0.75y - 1.25 $$

Esta forma permite visualizar con claridad cómo varía $z$ en función de $x$ y $y$, además de facilitar la representación gráfica del plano.

Ejemplo 2

Consideremos ahora la ecuación:

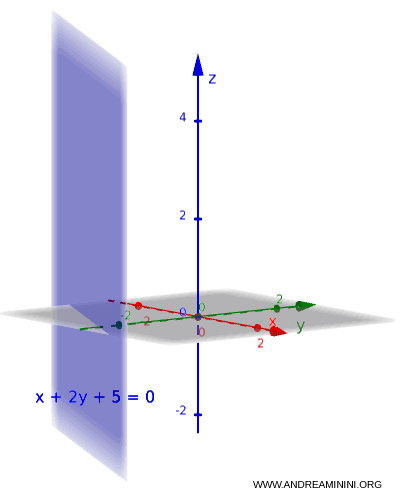
$x + 2y + 5 = 0$

Aquí, $c = 0$, por lo que la variable $z$ no aparece en la ecuación. El plano es paralelo al eje $z$ y no es posible escribirlo en forma explícita.

Plano que Pasa por un Punto Dado

Si se conoce un punto $P_0(x_0, y_0, z_0)$ y un vector normal $\vec{n} = (a, b, c)$, la ecuación del plano que pasa por dicho punto está dada por: $$ a(x - x_0) + b(y - y_0) + c(z - z_0) = 0 $$

Ejemplo

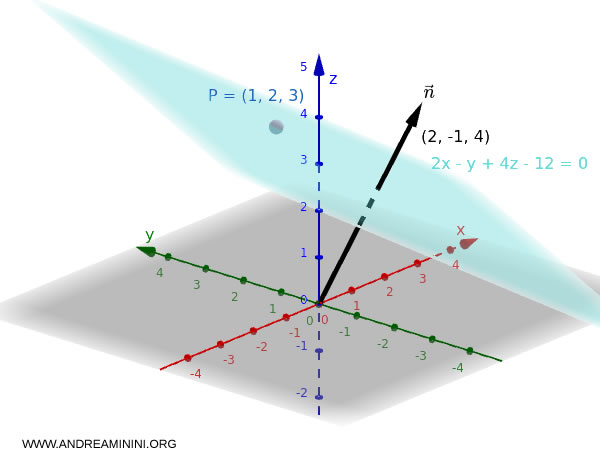
Sea $P = (1, 2, 3)$ y $\vec{n} = (2, -1, 4)$.

La ecuación del plano que pasa por $P$ es:

$$ 2(x - 1) - 1(y - 2) + 4(z - 3) = 0 $$

Desarrollando y simplificando:

$$ 2x - 2 - y + 2 + 4z - 12 = 0 $$

$$ 2x - y + 4z - 12 = 0 $$

Esta es la ecuación del plano que pasa por $P = (1, 2, 3)$ y es perpendicular al vector normal $\vec{n} = (2, -1, 4)$.

Distancia de un Punto a un Plano

Dado un plano $ax + by + cz + d = 0$ y un punto $P(x_1, y_1, z_1)$ en el espacio, la distancia mínima desde el punto al plano se calcula mediante la fórmula: $$ \text{Distancia} = \frac{|a x_1 + b y_1 + c z_1 + d|}{\sqrt{a^2 + b^2 + c^2}} $$

Ejemplo

Calculemos la distancia desde el punto $P = (1, 1, 1)$ hasta el plano $x + y + z - 3 = 0$:

$$ \text{Distancia} = \frac{|1 + 1 + 1 - 3|}{\sqrt{1^2 + 1^2 + 1^2}} = \frac{0}{\sqrt{3}} = 0 $$

Como la distancia es cero, el punto se encuentra sobre el plano.

Planos Especiales en el Espacio

En el espacio cartesiano, existen determinados planos que se consideran especiales porque sus ecuaciones solo involucran algunas variables, o porque carecen de ciertos coeficientes.

Planos Coordenados

Cuando la ecuación de un plano involucra únicamente una variable, dicho plano resulta paralelo a uno de los planos coordenados.

Los tres planos coordenados principales son:

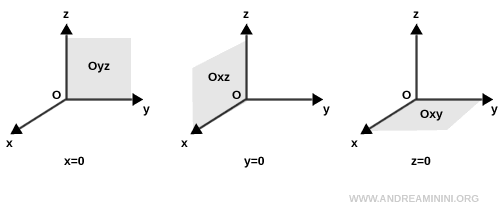
• El plano Oyz, definido cuando $ x = 0 $
• El plano Oxz, definido cuando $ y = 0 $
• El plano Oxy, definido cuando $ z = 0 $

Se denominan “planos coordenados” porque coinciden con los planos formados por dos de los tres ejes cartesianos.

Planos Paralelos a los Planos Coordenados

Si la ecuación adopta la forma $ x = k $, $ y = k $ o $ z = k $, el plano correspondiente es paralelo a uno de los planos coordenados.

• Si $ x = k $, el plano es paralelo al plano Oyz
• Si $ y = k $, el plano es paralelo al plano Oxz
• Si $ z = k $, el plano es paralelo al plano Oxy

En este caso, $ k $ es una constante real distinta de cero $ (k \ne 0) $.

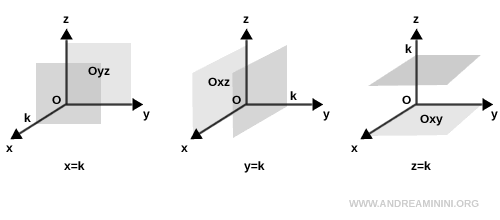
Estos planos mantienen la misma orientación que los planos coordenados, pero se encuentran desplazados a lo largo del eje correspondiente.

Planos con un Coeficiente Nulo

Cuando alguno de los coeficientes en la ecuación de un plano es cero, el plano resulta paralelo al eje asociado y perpendicular al plano formado por los otros dos ejes.

Consideremos la forma general de la ecuación de un plano:

$$ ax + by + cz + d = 0 $$

En particular:

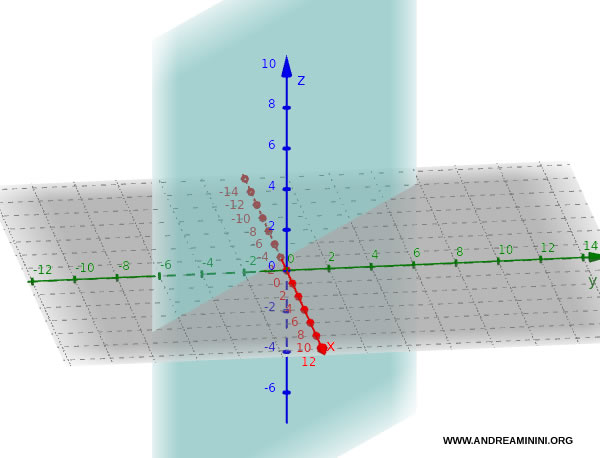
• Si $ c = 0 $, la ecuación se simplifica a $ ax + by + d = 0 $. El plano es paralelo al eje z y perpendicular al plano Oxy.

  Por ejemplo, el plano $ 3x + 4y + 0 \cdot z + 5 = 0 $, o simplemente $ 3x + 4y + 5 = 0 $, es paralelo al eje z y perpendicular al plano Oxy.
  

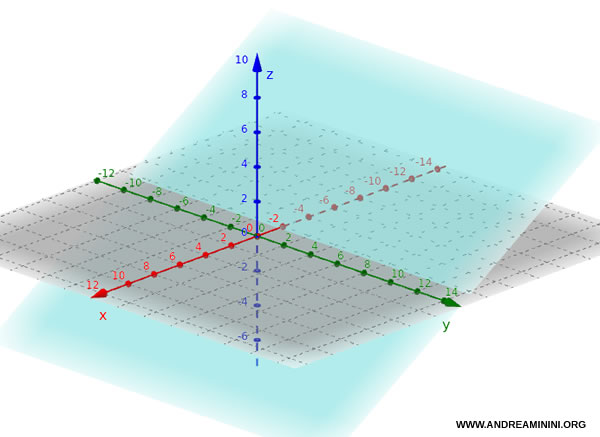
• Si $ b = 0 $, la ecuación se simplifica a $ ax + cz + d = 0 $. El plano es paralelo al eje y y perpendicular al plano Oxz.

  Por ejemplo, el plano $ 3x + 0 \cdot y + 5z + 5 = 0 $, o simplemente $ 3x + 5z + 5 = 0 $, es paralelo al eje y y perpendicular al plano Oxz.
  

• Si $ a = 0 $, la ecuación se simplifica a $ by + cz + d = 0 $. El plano es paralelo al eje x y perpendicular al plano Oyz.

  Por ejemplo, el plano $ 0 \cdot x + 4y + 5z + 5 = 0 $, o simplemente $ 4y + 5z + 5 = 0 $, es paralelo al eje x y perpendicular al plano Oyz.
  

Ecuaciones Paramétricas de un Plano

Un plano también puede describirse mediante ecuaciones paramétricas, utilizando dos vectores linealmente independientes contenidos en él y un punto de referencia: $$ \vec{r}(s,t) = P_0 + s \cdot \vec{v_1} + t \cdot \vec{v_2} $$ Aquí, $s, t \in \mathbb{R}$ son los parámetros, $P_0 = (x_0, y_0, z_0)$ es el punto, y $\vec{v_1}$ y $\vec{v_2}$ son vectores directores contenidos en el plano.

Ejemplo

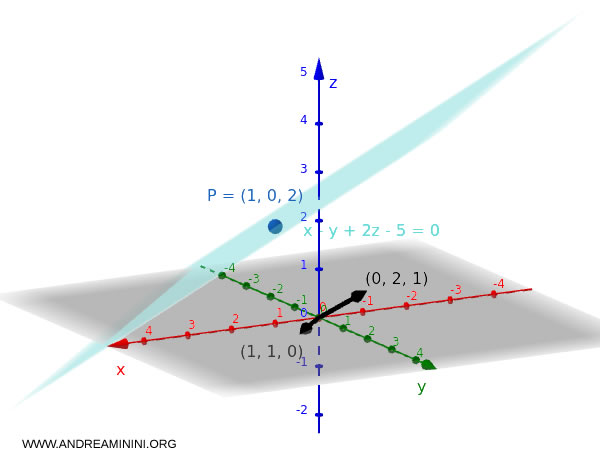
Sea $P_0 = (1, 0, 2)$, $\vec{v_1} = (1, 1, 0)$ y $\vec{v_2} = (0, 2, 1)$.

La ecuación paramétrica del plano es:

$$ \vec{r}(s,t) = (1,0,2) + s(1,1,0) + t(0,2,1) $$

Desarrollada en forma cartesiana:

$$ \begin{cases} x = 1 + s \\ y = s + 2t \\ z = 2 + t \end{cases} $$

Este sistema describe el mismo plano, siendo $s$ y $t$ parámetros libres.

Para expresar el plano en forma cartesiana (implícita), se eliminan los parámetros.

De la primera ecuación, se obtiene: $s = x - 1$

$$ \begin{cases} s = x - 1 \\ y = s + 2t \\ z = 2 + t \end{cases} $$

De la tercera ecuación: $t = z - 2$

$$ \begin{cases} s = x - 1 \\ y = s + 2t \\ t = z - 2 \end{cases} $$

Sustituyendo en la segunda ecuación:

$$ y = (x - 1) + 2(z - 2) = x + 2z - 5 $$

Así, la ecuación explícita del plano es:

$$ y = x + 2z - 5 $$

Reescribiéndola en forma general (implícita):

$$ x - y + 2z - 5 = 0 $$

Verificación: Comprobemos si el punto $P_0 = (1, 0, 2)$ pertenece al plano. Sustituyendo sus coordenadas en la ecuación $x - y + 2z - 5 = 0$: $$ 1 - 0 + 2 \cdot 2 - 5 = 1 + 4 - 5 = 0 $$ Como la igualdad se cumple, el punto está efectivamente sobre el plano.

Demostración

Para deducir la ecuación general de un plano, consideremos un plano $ \alpha $ que no pasa por el origen $ O(0, 0, 0) $ del sistema de coordenadas cartesianas.

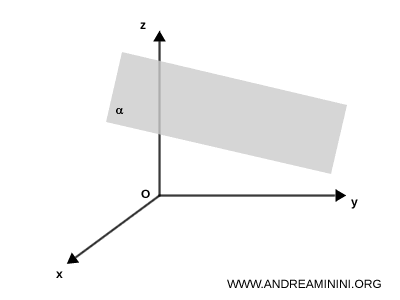
Se traza un vector perpendicular al plano $ \alpha $, que lo corta en el punto $ A = (a, b, c) $.

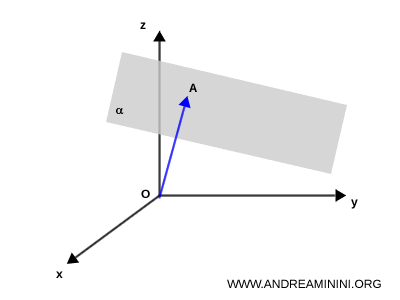
Esto implica que el segmento $ OA $ es perpendicular al plano $ \alpha $.

Elegimos ahora un punto cualquiera $ P = (x, y, z) $ que pertenezca al plano y sea distinto de $ A = (a, b, c) $.

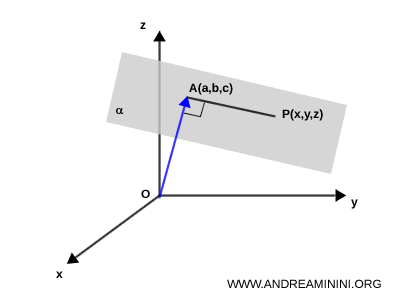
Como $ OA $ es perpendicular al plano y $ P $ se encuentra en él, el vector $ \vec{AP} $ es perpendicular a $ \vec{OA} $.

Conectamos el punto $ O $ con $ P $, formando el segmento $ OP $.

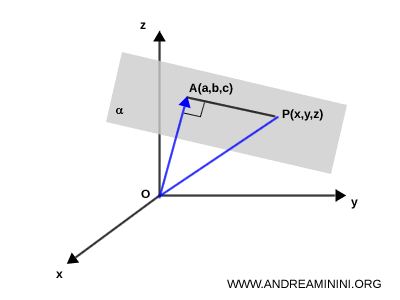
Como consecuencia, el triángulo $ \triangle OAP $ es un triángulo rectángulo por construcción.

Aplicando el teorema de Pitágoras, se obtiene la siguiente relación:

$$ OP^2 = OA^2 + AP^2 $$

Empleamos la fórmula de la distancia en el espacio tridimensional:

$$ \text{Distancia}^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2 $$

La distancia al cuadrado entre el origen $ O(0, 0, 0) $ y el punto $ A(a, b, c) $ es:

$$ OA^2 = a^2 + b^2 + c^2 $$

La distancia al cuadrado entre el origen y el punto $ P(x, y, z) $ es:

$$ OP^2 = x^2 + y^2 + z^2 $$

La distancia al cuadrado entre $ A(a, b, c) $ y $ P(x, y, z) $ es:

$$ AP^2 = (x - a)^2 + (y - b)^2 + (z - c)^2 $$

Sustituyendo en la identidad pitagórica:

$$ x^2 + y^2 + z^2 = a^2 + b^2 + c^2 + (x - a)^2 + (y - b)^2 + (z - c)^2 $$

Desarrollamos los binomios cuadrados:

$$ x^2 + y^2 + z^2 = a^2 + b^2 + c^2 + x^2 - 2ax + a^2 + y^2 - 2by + b^2 + z^2 - 2cz + c^2 $$

Reorganizamos y simplificamos términos semejantes:

$$ x^2 + y^2 + z^2 - a^2 - b^2 - c^2 - x^2 + 2ax - a^2 - y^2 + 2by - b^2 - z^2 + 2cz - c^2 = 0 $$

Agrupando términos semejantes:

$$ -2a^2 - 2b^2 - 2c^2 + 2ax + 2by + 2cz = 0 $$

Dividimos toda la ecuación entre 2:

$$ -a^2 - b^2 - c^2 + ax + by + cz = 0 $$

Que puede reescribirse así:

$$ ax + by + cz - (a^2 + b^2 + c^2) = 0 $$

Si definimos $ d = - (a^2 + b^2 + c^2) $, obtenemos la ecuación general del plano:

$$ ax + by + cz + d = 0 $$

Y así sucesivamente.