Semi-Plano
Un semi-plano es cada una de las dos partes en las que un plano queda dividido por una recta, conocida como “eje del semi-plano” o “borde/origen del semi-plano”.
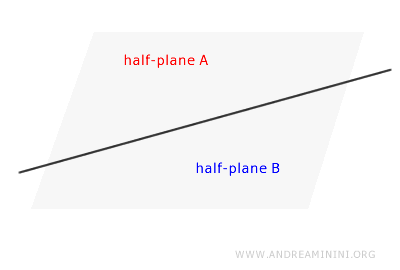
Por ejemplo, si dibujo una recta sobre una hoja de papel, se generan dos semi-planos opuestos: uno situado a la izquierda de la recta y otro a la derecha.
Cada semi-plano constituye un conjunto infinito de puntos. Los puntos que se encuentran en el interior de un semi-plano, pero no sobre su borde, se denominan puntos interiores del semi-plano.
Nota: En términos generales, un semi-plano incluye tanto los puntos del interior de una de las regiones en que queda dividido el plano, como los puntos que se encuentran sobre el eje que lo delimita.
Postulados de los Semi-Planos
Un semi-plano debe cumplir las propiedades establecidas en el postulado de partición del plano por una recta.
Dada una recta que divide el plano en dos conjuntos de puntos que no pertenecen a ella:
- Si tomamos dos puntos P y Q en la misma región, el segmento que los une no corta la recta.
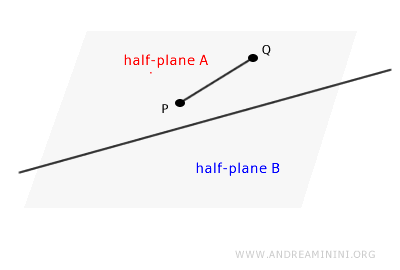
- Si tomamos dos puntos P y Q situados en regiones distintas, el segmento que los une necesariamente corta la recta.
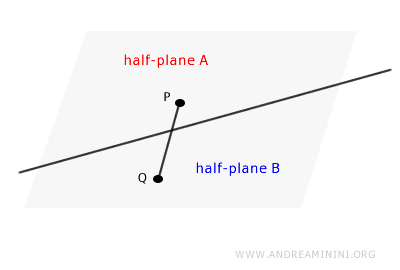
Si un conjunto de puntos satisface este postulado, se considera un semi-plano.
Tipos de Semi-Planos
Existen dos tipos de semi-planos:
- Semi-plano Abierto
Un semi-plano abierto no incluye la recta que lo delimita. Está formado únicamente por los puntos situados en su interior. - Semi-plano Cerrado
Un semi-plano cerrado incluye la recta divisoria. Comprende tanto los puntos interiores como los puntos que se encuentran sobre la recta que lo delimita.
Así, en el caso de un plano dividido en dos semi-planos cerrados, los puntos situados sobre el eje del semi-plano se consideran pertenecientes a ambos semi-planos.
Y así sucesivamente.