Planos Paralelos, Coincidentes e Intersecantes en el Espacio
Dos planos en R3 pueden ser paralelos, coincidentes o intersecantes.
- Son planos paralelos si no tienen ningún punto en común.
- Son planos coincidentes si, además de ser paralelos, comparten todos sus puntos.
- Son planos intersecantes si tienen en común infinitos puntos dispuestos sobre su recta de intersección.
En términos sencillos, cuando dos planos se intersecan, su intersección siempre es una recta. Por el contrario, si son paralelos o coincidentes, la intersección o bien no existe o coincide con todo el plano.
Nota: Los planos paralelos y coincidentes comparten la misma dirección normal, aunque difieren en su posición relativa. En cambio, los planos intersecantes se cortan a lo largo de una recta común, y sus vectores normales no son paralelos.
Cómo Determinar si Dos Planos son Paralelos, Coincidentes o Intersecantes
Para determinar si dos planos en el espacio son paralelos, coincidentes o intersecantes, es necesario analizar la dependencia lineal de los vectores directores de los planos.
- Si los vectores son linealmente dependientes, los planos son paralelos o coincidentes.
- Si los vectores son linealmente independientes, los planos se intersecan.
¿Cómo se verifica la dependencia lineal de los vectores?
Los dos planos se representan mediante sus ecuaciones vectoriales o paramétricas.
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t_1 \begin{pmatrix} l_1 \\ m_1 \\ n_1 \end{pmatrix} + t_2 \begin{pmatrix} l_2 \\ m_2 \\ n_2 \end{pmatrix} $$
$$ \begin{pmatrix} x' \\ y' \\ z' \end{pmatrix} = \begin{pmatrix} x'_0 \\ y'_0 \\ z'_0 \end{pmatrix} + t_1 \begin{pmatrix} l_3 \\ m_3 \\ n_3 \end{pmatrix} + t_2 \begin{pmatrix} l_4 \\ m_4 \\ n_4 \end{pmatrix} $$
Se toman los cuatro vectores directores y se disponen en una matriz.
$$ \begin{pmatrix} l_1 & l_2 & l_3 & l_4 \\ m_1 & m_2 & m_3 & m_4 \\ n_1 & n_2 & n_3 & n_4 \end{pmatrix} $$
Después se calcula el rango de la matriz.
- Si el rango de la matriz es igual o menor que 2, los vectores son linealmente dependientes. En este caso, los planos son paralelos o coincidentes. $$ r_k \begin{pmatrix} l_1 & l_2 & l_3 & l_4 \\ m_1 & m_2 & m_3 & m_4 \\ n_1 & n_2 & n_3 & n_4 \end{pmatrix} \le 2 $$
Nota: Para distinguir entre planos paralelos y coincidentes, basta verificar si algún punto de uno de los planos pertenece también al otro. Si el punto está en ambos, los planos son coincidentes. De lo contrario, son paralelos.
- Si el rango de la matriz es 3, los vectores son linealmente independientes y, por tanto, los planos se intersecan. $$ r_k \begin{pmatrix} l_1 & l_2 & l_3 & l_4 \\ m_1 & m_2 & m_3 & m_4 \\ n_1 & n_2 & n_3 & n_4 \end{pmatrix} = 3 $$
Así que, cuando las ecuaciones de los planos se expresan en forma paramétrica, se aplica la siguiente regla:
| Rango de la Matriz | Relación entre Vectores | Posición Relativa de los Planos |
|---|---|---|
| 1 - 2 | Linealmente dependientes | Coincidentes o planos paralelos distintos |
| 3 | Linealmente independientes | Planos intersecantes (se cortan en una recta) |
El Caso de las Ecuaciones Cartesianas
Para planos definidos mediante ecuaciones cartesianas
$$ a_1 x + b_1 y + c_1 z + d_1 = 0 $$
$$ a_2 x + b_2 y + c_2 z + d_2 = 0 $$
los vectores son linealmente dependientes si el rango de la matriz de coeficientes es 1.
En tal caso, los planos son paralelos o coincidentes.
$$ r_k \begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{pmatrix} = 1 $$
Los vectores son linealmente independientes si el rango de la matriz de coeficientes es 2.
En ese caso, los planos se intersecan.
$$ r_k \begin{pmatrix} a_1 & b_1 & c_1 \\ a_2 & b_2 & c_2 \end{pmatrix} = 2 $$
Así que, para ecuaciones cartesianas de planos, la regla a seguir es la siguiente:
| Rango de la Matriz | Relación entre Vectores | Posición Relativa de los Planos |
|---|---|---|
| 1 | Linealmente dependientes | Coincidentes o planos paralelos distintos |
| 2 | Linealmente independientes | Planos intersecantes (se cortan en una recta) |
Ejemplo
Ejemplo 1 (Ecuaciones Paramétricas)
Consideremos dos planos en el espacio:
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -1 \\ 2 \end{pmatrix} + t_2 \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} $$
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -3 \\ 6 \end{pmatrix} + t_2 \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} $$
Colocamos los vectores directores en una matriz.
Después calculamos su rango.
$$ r_k \begin{pmatrix} 0 & 2 & 0 & 1 \\ -1 & -1 & -3 & -1 \\ 2 & 0 & 6 & 1 \end{pmatrix} = 2 $$
El rango de la matriz es 2.
Por tanto, los vectores resultan linealmente dependientes.
Esto indica que los planos son paralelos o coincidentes.
¿Cómo determinar si los planos son paralelos o coincidentes?
Para averiguarlo, basta tomar un punto de uno de los planos y comprobar si pertenece al otro.
Sabemos que el punto P(0,0,0) pertenece al primer plano:
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -1 \\ 2 \end{pmatrix} + t_2 \begin{pmatrix} 2 \\ -1 \\ 0 \end{pmatrix} $$
Sustituimos las coordenadas (0,0,0) en la ecuación del segundo plano y verificamos si se cumple:
$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -3 \\ 6 \end{pmatrix} + t_2 \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} $$
$$ \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} = \begin{pmatrix} 0 \\ 1 \\ 0 \end{pmatrix} + t_1 \begin{pmatrix} 0 \\ -3 \\ 6 \end{pmatrix} + t_2 \begin{pmatrix} 1 \\ -1 \\ 1 \end{pmatrix} $$
Esto se traduce en el siguiente sistema de ecuaciones:
$$ \begin{cases} 0 = 0 + t_2 \\ 0 = 1 - 3t_1 - t_2 \\ 0 = 0 + 6t_1 + t_2 \end{cases} $$
$$ \begin{cases} t_2 = 0 \\ 1 - 3t_1 = 0 \\ 6t_1 = 0 \end{cases} $$
$$ \begin{cases} t_2 = 0 \\ t_1 = \frac{1}{3} \\ t_1 = 0 \end{cases} $$
El sistema es incompatible, pues da valores contradictorios para \( t_1 \).
Esto demuestra que el punto P(0,0,0) no pertenece al segundo plano, por lo que los planos no son coincidentes.
Por lo tanto, se trata de planos paralelos.
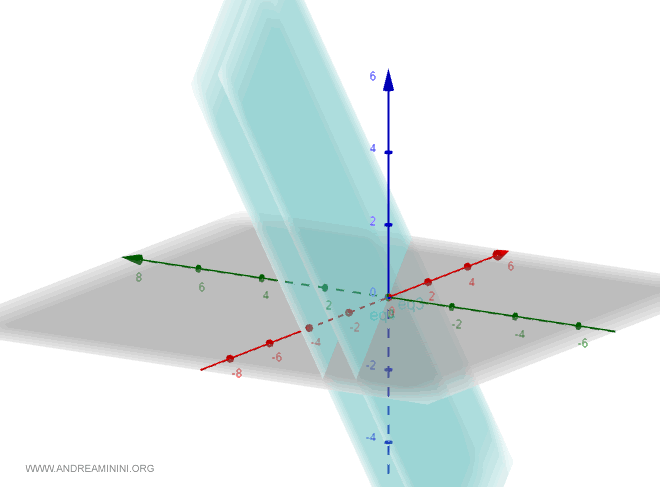
Ejemplo 2 (Ecuaciones Cartesianas)
Analicemos ahora dos ecuaciones cartesianas:
$$ x + 2y + z = 0 $$
$$ 2x + 4y + 2z - 5 = 0 $$
Formamos la matriz de coeficientes:
$$ \begin{pmatrix} 1 & 2 & 1 \\ 2 & 4 & 2 \end{pmatrix} $$
y calculamos su rango:
$$ r_k \begin{pmatrix} 1 & 2 & 1 \\ 2 & 4 & 2 \end{pmatrix} = 1 $$
El rango de la matriz es 1.
Por tanto, los vectores normales son linealmente dependientes, lo que significa que los planos son paralelos o coincidentes.
¿Cómo determinar si son paralelos o coincidentes?
Para verificarlo, podemos hallar un punto del primer plano, fijando dos coordenadas en cero.
Por ejemplo, si x=0 e y=0:
$$ x + 2y + z = 0 $$
$$ 0 + 2·0 + z = 0 $$
$$ z = 0 $$
Así, obtenemos el punto:
$$ P(x, y, z) = P(0, 0, 0) $$
Sustituimos las coordenadas de este punto en la ecuación del segundo plano:
$$ 2x + 4y + 2z - 5 = 0 $$
$$ 2(0) + 4(0) + 2(0) - 5 = 0 $$
$$ -5 = 0 $$
La igualdad no se cumple.
Por tanto, el punto P(0,0,0) del primer plano no pertenece al segundo.
En consecuencia, los planos no son coincidentes.
Se concluye que se trata de planos paralelos.
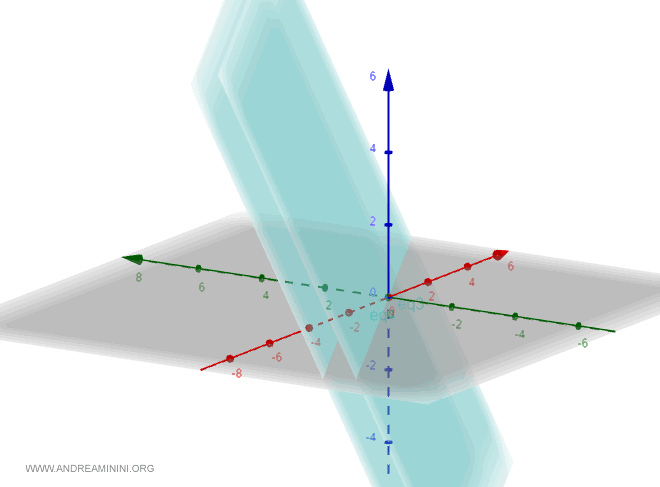
Notas Adicionales
Algunos apuntes adicionales sobre planos paralelos o inclinados:
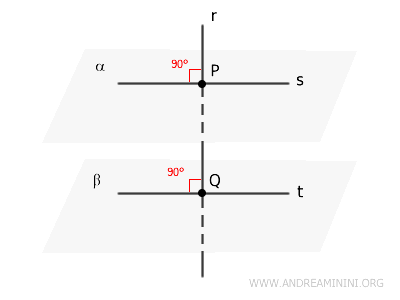
- Teorema de la Recta Perpendicular a Dos Planos
Si dos planos \( \alpha \) y \( \beta \) son perpendiculares a una misma recta \( r \) en dos puntos distintos \( P \) y \( Q \), dichos planos son necesariamente paralelos.
- Teorema de los Planos Paralelos Intersecados por un Tercer Plano
Cuando un plano \( \pi \) interseca a dos planos paralelos \( \pi_1 \) y \( \pi_2 \), se obtienen dos rectas paralelas como intersección.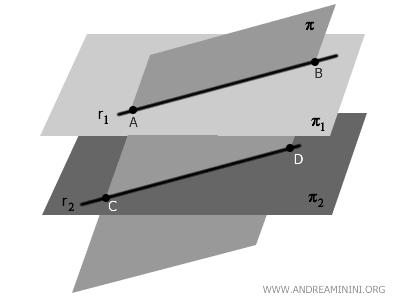
Esto ocurre porque \( \pi_1 \) y \( \pi_2 \) son paralelos y equidistantes, lo que implica que el plano \( \pi \) los corta generando dos rectas \( r_1 \) y \( r_2 \). Al intersectar ambos planos con el mismo ángulo, las rectas \( r_1 \) y \( r_2 \) resultan necesariamente paralelas.
Y así sucesivamente.