Teorema de los planos paralelos cortados por un tercer plano

Cuando un plano $ \pi $ corta a dos planos paralelos $ \pi_1 $ y $ \pi_2 $, las intersecciones son dos rectas paralelas $ r_1 $ y $ r_2 $.
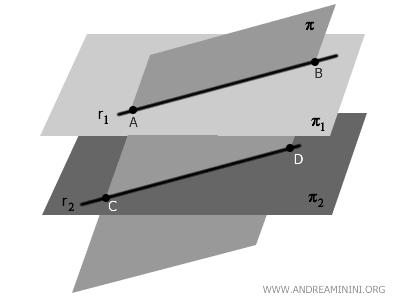
demostración

Esto ocurre porque $ \pi_1 $ y $ \pi_2 $ son paralelos y equidistantes. Al cortar ambos planos, el plano $ \pi $ genera dos rectas de intersección $ r_1 $ y $ r_2 $, una en cada plano.

Como la inclinación con la que $ \pi $ intersecta a $ \pi_1 $ y $ \pi_2 $ es la misma, las rectas de intersección resultan ser paralelas entre sí.

Demostración

Sea $ \pi_1 $ y $ \pi_2 $ un par de planos paralelos.

Por definición, la distancia entre ellos es constante y sus vectores normales son proporcionales.

Supongamos ahora que un tercer plano $ \pi $ intersecta a $ \pi_1 $ en la recta $ r_1 $, y a $ \pi_2 $ en la recta $ r_2 $.

demostración

Como los planos $ \pi_1 $ y $ \pi_2 $ son paralelos, el plano $ \pi $ los corta con el mismo ángulo, es decir, sin variar su inclinación respecto a cada uno.

Las rectas $ r_1 $ y $ r_2 $, al estar determinadas por la intersección del mismo plano $ \pi $ con planos paralelos, se encuentran en el mismo plano y son coplanarias.

Consideremos dos puntos $ A $ y $ B $ sobre la recta $ r_1 $, y sus respectivas proyecciones ortogonales $ A' $ y $ B' $ sobre la recta $ r_2 $, ubicadas en el plano $ \pi_2 $.

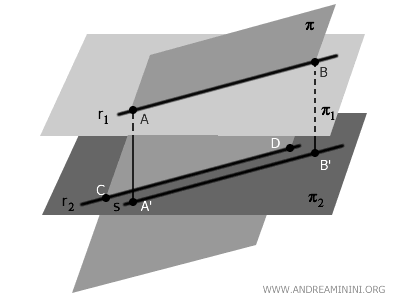
ejemplo

Los segmentos perpendiculares $ AA' $ y $ BB' $ representan la distancia constante entre los planos $ \pi_1 $ y $ \pi_2 $, por lo tanto son paralelos y congruentes:

$$ AA' \parallel BB', \quad AA' \cong BB' $$

Como ambos pares de puntos están conectados por segmentos perpendiculares y congruentes, y como las rectas $ r_1 $ y $ r_2 $ están contenidas en un mismo plano y tienen la misma dirección, se concluye que:

$$ r_1 \parallel r_2 $$

En resumen, las rectas de intersección generadas por un plano que corta a dos planos paralelos son también paralelas, ya que:

pertenecen al mismo plano $ \pi $,
conservan la misma orientación,
y están separadas por una distancia constante determinada por la separación entre $ \pi_1 $ y $ \pi_2 $.

Y así sucesivamente.