Teorema de Intersección de Planos
Cuando dos planos distintos se intersecan en el espacio en un punto $P$, comparten una recta $r$ que pasa por dicho punto.
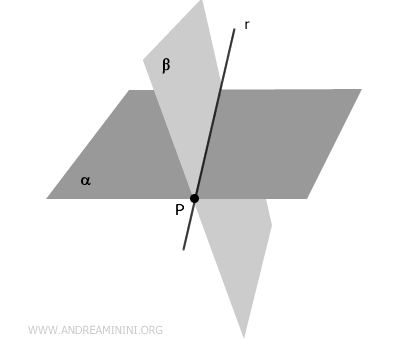
En términos sencillos, dos planos que se intersecan no pueden coincidir únicamente en un solo punto. Siempre comparten, al menos, una recta común.
La recta compartida por ambos planos está formada por todos aquellos puntos que pertenecen simultáneamente a los dos planos.
Este resultado se basa en principios fundamentales de la geometría tridimensional, que establecen que la intersección de dos planos no paralelos en el espacio siempre forma una recta.
Demostración
Consideremos dos planos, \( \alpha \) y \( \beta \), que se intersecan en un punto \( P \).
$$ P \in \alpha \cap \beta $$
Esto significa que el punto \( P \) pertenece tanto al plano \( \alpha \) como al plano \( \beta \).

Supongamos ahora dos puntos, $A$ y $B$, situados sobre el plano $ \alpha $, pero en lados opuestos respecto al plano $ \beta $.
Se traza el segmento $ \overline{AB} $ que une los puntos $A$ y $B$.
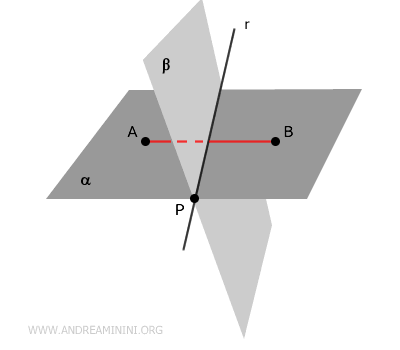
Dado que los planos se intersecan, y puesto que el segmento $ \overline{AB} $ se extiende a través de ambos semiplanos de $ \alpha $, necesariamente corta al plano $ \beta $ en algún punto $C$.
En este punto, hemos identificado dos puntos que pertenecen a ambos planos: el punto original $P$ y el nuevo punto $C$.
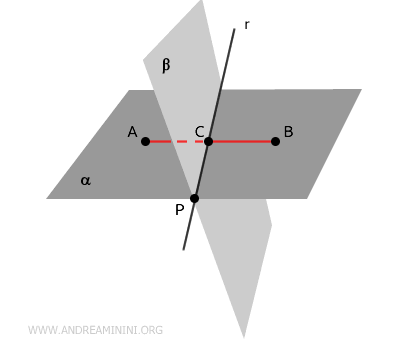
Por dos puntos distintos siempre puede trazarse una única recta, que en este caso está contenida en ambos planos.
Así queda demostrado que, si dos planos se intersecan en un punto \( P \), necesariamente comparten también una recta \( r \) que pasa por dicho punto.
Con esto, el teorema queda probado.