Ecuación de un Plano que Pasa por Tres Puntos No Colineales

Dados tres puntos no colineales en el espacio R³, existe un único plano que pasa por ellos: P₁, P₂ y P₃. $$ P_1 \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} \:\:\: P_2 \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} \:\:\: P_3 \begin{pmatrix} x_3 \\ y_3 \\ z_3 \end{pmatrix} $$

Cómo Determinar las Ecuaciones Paramétricas de un Plano

Si tenemos tres puntos $ P_1(x_1,y_1,z_1) $, $ P_2(x_2,y_2,z_2) $ y $ P_3(x_3,y_3,z_3) $, y el plano no es paralelo al eje z, puede expresarse en forma explícita como:

$$ z = mx + ny + q $$

Al sustituir las coordenadas de los tres puntos, se obtiene un sistema de tres ecuaciones:

$$ \begin{cases} mx_1 + ny_1 + q = z_1 \\ mx_2 + ny_2 + q = z_2 \\ mx_3 + ny_3 + q = z_3 \end{cases} $$

Resolver este sistema permite determinar los valores de $ m $, $ n $ y $ q $, que definen la ecuación del plano.

Nota. Este método solo es válido si el plano puede expresarse en forma explícita, es decir, si no es vertical (paralelo al eje $ z $).

¿Cómo saber si el sistema tiene solución?

Para comprobar si el sistema admite solución - es decir, si los tres puntos determinan un plano que pueda escribirse como $ z = mx + ny + q $ - se puede reescribir el sistema en forma matricial:

$$
\begin{bmatrix}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1
\end{bmatrix}
\cdot
\begin{bmatrix}
m \\
n \\
q
\end{bmatrix}
=
\begin{bmatrix}
z_1 \\
z_2 \\
z_3
\end{bmatrix}
$$

Aquí, $ A $ es la matriz de coeficientes:

$$
A =
\begin{bmatrix}
x_1 & y_1 & 1 \\
x_2 & y_2 & 1 \\
x_3 & y_3 & 1
\end{bmatrix}
$$

El sistema tiene una única solución si el determinante de $ A $ es distinto de cero:

$\det(A) \ne 0$

Si $ \det(A) \ne 0 $, significa que el plano no es paralelo al eje $ z $, y puede escribirse en forma explícita.

En cambio, si $ \det(A) = 0 $, el plano es vertical y no puede expresarse de forma explícita. No obstante, siempre es posible obtener su ecuación implícita en la forma $ ax + by + cz + d = 0 $ mediante otro procedimiento.

¿Qué significa geométricamente que $ \det(A) = 0 $? Si el determinante es cero, significa que las proyecciones de los tres puntos sobre el plano $ xy $ están alineadas, es decir, que los puntos proyectados $ (x_i, y_i) $ se sitúan sobre una misma recta. En tal caso, el plano se considera “vertical” y no puede representarse en la forma $ z = mx + ny + q $.

Ejemplo

Consideremos tres puntos no colineales en el espacio:

$$ P_1 \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} \:\:\: P_2 \begin{pmatrix} 2 \\ 0 \\ 3 \end{pmatrix} \:\:\: P_3 \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} $$

Podemos plantear el siguiente sistema de ecuaciones a partir de sus coordenadas:

$$ \begin{cases} mx_1 + ny_1 + q = z_1 \\ mx_2 + ny_2 + q = z_2 \\ mx_3 + ny_3 + q = z_3 \end{cases} $$

$$ \begin{cases} m(1) + n(3) + q = 5 \\ m(2) + n(0) + q = 3 \\ m(4) + n(1) + q =2 \end{cases} $$

$$ \begin{cases} m + 3n + q = 5 \\ 2m + q = 3 \\ 4m + n + q =2 \end{cases} $$

La matriz de coeficientes $ A $ es:

$$
A =
\begin{bmatrix}
1 & 3 & 1 \\
2 & 0 & 1 \\
4 & 1 & 1
\end{bmatrix}
$$

Calculamos su determinante:

$$ \Delta = (1 \cdot 0 \cdot 1) + (3 \cdot 1 \cdot 4) + (1 \cdot 2 \cdot 1) - (1 \cdot 0 \cdot 4) - (3 \cdot 2 \cdot 1) - (1 \cdot 1 \cdot 1) $$

$$ \Delta = 0 + 12 + 2 - 0 - 6 - 1 = 7 $$

Como $ \Delta = 7 \ne 0 $, el sistema admite solución única.

$$ \begin{cases} m + 3n + q = 5 \\ 2m + q = 3 \\ 4m + n + q = 2 \end{cases} $$

Procedemos a resolverlo mediante la Regla de Cramer.

Primero, sustituimos la primera columna por los términos independientes $ (5,3,2) $:

$$ \Delta_m = \begin{vmatrix} 5 & 3 & 1 \\ 3 & 0 & 1 \\ 2 & 1 & 1 \end{vmatrix} $$

$$ \Delta_m = 5 \cdot \begin{vmatrix} 0 & 1 \\ 1 & 1 \end{vmatrix} - 3 \cdot \begin{vmatrix} 3 & 1 \\ 2 & 1 \end{vmatrix} + 1 \cdot \begin{vmatrix} 3 & 0 \\ 2 & 1 \end{vmatrix} $$

$$ \Delta_m = 5(-1) - 3(1) + 1(3) = -5 - 3 + 3 $$

$$ \Delta_m = -5 $$

Después sustituimos la segunda columna:

$$ \Delta_n = \begin{vmatrix} 1 & 5 & 1 \\ 2 & 3 & 1 \\ 4 & 2 & 1 \end{vmatrix} $$

$$ \Delta_n = 1 \cdot \begin{vmatrix} 3 & 1 \\ 2 & 1 \end{vmatrix} - 5 \cdot \begin{vmatrix} 2 & 1 \\ 4 & 1 \end{vmatrix} + 1 \cdot \begin{vmatrix} 2 & 3 \\ 4 & 2 \end{vmatrix} $$

$$ \Delta_n = 1(1) - 5(-2) + 1(-8) = 1 + 10 - 8 $$

$$ \Delta_n = 3 $$

Por último, sustituimos la tercera columna:

$$ \Delta_q = \begin{vmatrix} 1 & 3 & 5 \\ 2 & 0 & 3 \\ 4 & 1 & 2 \end{vmatrix} $$

$$ \Delta_q = 1 \cdot \begin{vmatrix} 0 & 3 \\ 1 & 2 \end{vmatrix} - 3 \cdot \begin{vmatrix} 2 & 3 \\ 4 & 2 \end{vmatrix} + 5 \cdot \begin{vmatrix} 2 & 0 \\ 4 & 1 \end{vmatrix} $$

$$ \Delta_q = 1(-3) - 3(-8) + 5(2) = -3 + 24 + 10 $$

$$ \Delta_q = 31 $$

Aplicando la Regla de Cramer:

$$ m = \frac{\Delta_m}{\Delta} = \frac{-5}{7} $$

$$ n = \frac{\Delta_n}{\Delta} = \frac{3}{7} $$

$$ q = \frac{\Delta_q}{\Delta} = \frac{31}{7} $$

Por tanto, el resultado final es:

$$ \begin{cases} m = -\frac{5}{7} \\ n = \frac{3}{7} \\ q = \frac{31}{7} \end{cases} $$

Al sustituir $ m $, $ n $ y $ q $ en la ecuación explícita del plano $ z = mx + ny + q $, se obtiene:

$$ -\frac{5}{7} x + \frac{3}{7}y + \frac{31}{7} = z $$

Ésta es la ecuación del plano que pasa por los puntos $ P_1 \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} \:\:\: P_2 \begin{pmatrix} 2 \\ 0 \\ 3 \end{pmatrix} \:\:\: P_3 \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} $

Un Método Alternativo y Más General

Este método alternativo permite determinar la ecuación general (implícita) de un plano a partir de tres puntos dados:

$a x + b y + c z + d = 0$

La gran ventaja de este procedimiento es que es aplicable en cualquier situación: tanto si el plano es vertical, horizontal u oblicuo, y además evita tener que resolver un sistema de ecuaciones.

La contrapartida es que requiere ciertos conceptos básicos de álgebra vectorial y cálculo vectorial.

¿Cómo se procede?

Partimos de las coordenadas de tres puntos en el espacio:

$$
P_1(x_1,y_1,z_1), \quad
P_2(x_2,y_2,z_2), \quad
P_3(x_3,y_3,z_3)
$$

A partir de ellos, construimos dos vectores directores contenidos en el plano:

$$ \vec{v_1} = P_2 - P_1 = (x_2 - x_1, \ y_2 - y_1, \ z_2 - z_1) $$

$$ \vec{v_2} = P_3 - P_1 = (x_3 - x_1, \ y_3 - y_1, \ z_3 - z_1) $$

Luego calculamos el producto vectorial $ \vec{n} = \vec{v_1} \times \vec{v_2} $, que nos proporciona un vector normal al plano:

$$
\vec{n} = (a, b, c) =
\left|
\begin{matrix}
\mathbf{i} & \mathbf{j} & \mathbf{k} \\
x_2 - x_1 & y_2 - y_1 & z_2 - z_1 \\
x_3 - x_1 & y_3 - y_1 & z_3 - z_1
\end{matrix}
\right|
$$

Las componentes de este vector normal corresponden precisamente a los coeficientes $ a $, $ b $ y $ c $ de la ecuación general del plano.

Otra forma de calcular directamente estos coeficientes es mediante las siguientes fórmulas:

$$ a = (y_2 - y_1)(z_3 - z_1) - (y_3 - y_1)(z_2 - z_1) $$

$$ b = (z_2 - z_1)(x_3 - x_1) - (z_3 - z_1)(x_2 - x_1) $$

$$ c = (x_2 - x_1)(y_3 - y_1) - (x_3 - x_1)(y_2 - y_1) $$

Una vez determinados $ a $, $ b $ y $ c $, podemos expresar la ecuación general del plano utilizando cualquiera de los tres puntos dados:

$$ a (x - x_1) + b (y - y_1) + c (z - z_1) = 0 $$

O bien, desarrollarla para obtener la ecuación completamente implícita:

$$ a x + b y + c z + d = 0 $$

donde la constante $ d $ se calcula así:

$$ d = - (a x_1 + b y_1 + c z_1) $$

Ambas formas describen la ecuación general del plano.

Además, si $ c \ne 0 $, podemos despejar $ z $ para escribir la ecuación en forma explícita:

$$ z = - \frac{a}{c} x - \frac{b}{c} y - \frac{d}{c} $$

Por supuesto, esto solo es posible si $ c \ne 0 $. Si $ c = 0 $, el plano es vertical respecto al eje $ z $ y no puede expresarse en forma explícita.

Ejemplo

Consideremos nuevamente los mismos tres puntos usados en el ejemplo anterior:

$$
P_1 = (1, 3, 5), \quad
P_2 = (2, 0, 3), \quad
P_3 = (4, 1, 2)
$$

Primero, calculamos los vectores directores del plano:

$$ \vec{v_1} = P_2 - P_1 = (2 - 1, \ 0 - 3, \ 3 - 5) = (1, \ -3, \ -2) $$

$$ \vec{v_2} = P_3 - P_1 = (4 - 1, \ 1 - 3, \ 2 - 5) = (3, \ -2, \ -3) $$

A continuación, calculamos el producto vectorial de estos dos vectores:

$$ \vec{n} = \vec{v_1} \times \vec{v_2} = (a, b, c) $$

Utilizando la regla del determinante:

$$ \vec{n} = \left| \begin{matrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 1 & -3 & -2 \\ 3 & -2 & -3 \end{matrix} \right| $$

$$ \vec{n} = \mathbf{i} \cdot \left| \begin{matrix}-3 & -2 \\ -2 & -3 \end{matrix} \right| - \mathbf{j} \cdot \left| \begin{matrix} 1 & -2 \\ 3 & -3 \end{matrix} \right| + \mathbf{k} \cdot \left| \begin{matrix} 1 & -3 \\ 3 & -2 \end{matrix} \right| $$

$$ \vec{n} = \mathbf{i} \cdot (9 - 4) - \mathbf{j} \cdot (-3 + 6) + \mathbf{k} \cdot (-2 - (-9)) $$

$$ \vec{n} = \mathbf{i} \cdot 5 - \mathbf{j} \cdot (-3) + \mathbf{k} \cdot 7 $$

$$ \vec{n} = 5 \mathbf{i} + 3 \mathbf{j} + 7 \mathbf{k} $$

Por tanto, el vector normal al plano es $ \vec{n} = (5, 3, 7) $.

Los coeficientes correspondientes son:

$$ a = 5, \quad b = 3, \quad c = 7 $$

Podemos escribir entonces la ecuación del plano:

$$ 5(x - 1) + 3(y - 3) + 7(z - 5) = 0 $$

Desarrollando los términos:

$$ 5x - 5 + 3y - 9 + 7z - 35 = 0 $$

$$ 5x + 3y + 7z - 49 = 0 $$

Así, la ecuación general del plano queda:

$$ 5x + 3y + 7z = 49 $$

Dado que el coeficiente de $ z $ es distinto de cero, podemos expresar la ecuación también en forma explícita.

Despejamos $ z $:

$$ 7z = -5x - 3y + 49 $$

Dividimos entre 7:

$$ z = -\frac{5}{7} x - \frac{3}{7} y + \frac{49}{7} $$

Esta es la ecuación explícita del plano que pasa por los tres puntos dados, coincidiendo exactamente con el resultado obtenido mediante el método anterior.

Método Vectorial

A partir de tres puntos, podemos determinar dos vectores directores:

$$ v_1 = P_1P_2 = \begin{pmatrix} x_2 \\ y_2 \\ z_2 \end{pmatrix} - \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \\ z_2 - z_1 \end{pmatrix} $$

$$ v_2 = P_1P_3 = \begin{pmatrix} x_3 \\ y_3 \\ z_3 \end{pmatrix} - \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} = \begin{pmatrix} x_3 - x_1 \\ y_3 - y_1 \\ z_3 - z_1 \end{pmatrix} $$

A continuación, debemos comprobar que estos vectores sean linealmente independientes.

Ambos vectores generan el plano y forman una base del espacio vectorial únicamente si son linealmente independientes.

Dos vectores son linealmente independientes si el rango de la matriz que se obtiene colocándolos en columnas es igual al número de vectores.

$$ r_k \begin{pmatrix} x_2 - x_1 & x_3 - x_1 \\ y_2 - y_1 & y_3 - y_1 \\ z_2 - z_1 & z_3 - z_1 \end{pmatrix} = 2 $$

Una vez comprobada la independencia lineal de los vectores, elegimos uno de los tres puntos como punto de referencia P₀ perteneciente al plano.

Por ejemplo, podemos elegir el punto P₁:

$$ P_0 = P_1 $$

$$ \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} = \begin{pmatrix} x_1 \\ y_1 \\ z_1 \end{pmatrix} $$

Con esta información, ya estamos en condiciones de escribir la ecuación vectorial del plano:

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = P_0 + t_1 \cdot v_1 + t_2 \cdot v_2 $$

donde $ t_1 $ y $ t_2 $ son parámetros de la ecuación vectorial que describen todos los puntos que pertenecen al plano.

Sustituyendo los dos vectores directores:

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = P_0 + t_1 \cdot \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \\ z_2 - z_1 \end{pmatrix} + t_2 \cdot \begin{pmatrix} x_3 - x_1 \\ y_3 - y_1 \\ z_3 - z_1 \end{pmatrix} $$

Y sustituyendo el punto P₀:

Así obtenemos la ecuación vectorial del plano:

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} + t_1 \cdot \begin{pmatrix} x_2 - x_1 \\ y_2 - y_1 \\ z_2 - z_1 \end{pmatrix} + t_2 \cdot \begin{pmatrix} x_3 - x_1 \\ y_3 - y_1 \\ z_3 - z_1 \end{pmatrix} $$

Para deducir la ecuación paramétrica del plano, transformamos la forma vectorial en un sistema de tres ecuaciones:

$$ \begin{cases} x = x_0 + t_1 \cdot ( x_2 - x_1 ) + t_2 \cdot ( x_3 - x_1 ) \\ y = y_0 + t_1 \cdot ( y_2 - y_1 ) + t_2 \cdot ( y_3 - y_1 ) \\ z = z_0 + t_1 \cdot ( z_2 - z_1 ) + t_2 \cdot ( z_3 - z_1 ) \end{cases} $$

Para encontrar la ecuación cartesiana, partimos de las ecuaciones paramétricas:

Desplazamos las coordenadas de P₀ al primer miembro:

$$ \begin{cases} x - x_0 = t_1 \cdot ( x_2 - x_1 ) + t_2 \cdot ( x_3 - x_1 ) \\ y - y_0 = t_1 \cdot ( y_2 - y_1 ) + t_2 \cdot ( y_3 - y_1 ) \\ z - z_0 = t_1 \cdot ( z_2 - z_1 ) + t_2 \cdot ( z_3 - z_1 ) \end{cases} $$

Luego se construye una matriz colocando las componentes de los tres vectores (el vector resultante y los dos vectores directores) como columnas:

$$ \begin{pmatrix} x-x_0 & x_2 - x_1 & x_3 - x_1 \\ y-y_0 & y_2 - y_1 & y_3 - y_1 \\ z-z_0 & z_2 - z_1 & z_3 - z_1 \end{pmatrix} $$

Finalmente, se calcula el determinante de la matriz y se iguala a cero:

$$ det \begin{pmatrix} x-x_0 & x_2 - x_1 & x_3 - x_1 \\ y-y_0 & y_2 - y_1 & y_3 - y_1 \\ z-z_0 & z_2 - z_1 & z_3 - z_1 \end{pmatrix} = 0 $$

$$ ( x-x_0 ) \cdot \begin{vmatrix} y_2-y_1 & y_3 - y_1 \\ z_2 - z_1 & z_3 - z_1 \end{vmatrix} - (y-y_0) \cdot \begin{vmatrix} x_2-x_1 & x_3 - x_1 \\ z_2 - z_1 & z_3 - z_1 \end{vmatrix} +(z-z_0) \cdot \begin{vmatrix} x_2-x_1 & x_3 - x_1 \\ y_2-y_1 & y_3 - y_1 \end{vmatrix} = 0$$

De este modo se obtiene la ecuación cartesiana del plano:

$$ ( x-x_0 ) \cdot a - (y-y_0) \cdot b +(z-z_0) \cdot c = 0$$

Ejemplo

Consideremos tres puntos no colineales en el espacio:

$$ P_1 \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} \:\:\: P_2 \begin{pmatrix} 2 \\ 0 \\ 3 \end{pmatrix} \:\:\: P_3 \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} $$

A partir de estos puntos obtenemos los vectores directores:

$$ v_1 = P_1P_2 = \begin{pmatrix} 2 \\ 0 \\ 3 \end{pmatrix} - \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} = \begin{pmatrix} 1 \\ -3 \\ -2 \end{pmatrix} $$

$$ v_2 = P_1P_3 = \begin{pmatrix} 4 \\ 1 \\ 2 \end{pmatrix} - \begin{pmatrix} 1 \\ 3 \\ 5 \end{pmatrix} = \begin{pmatrix} 3 \\ -2 \\ -3 \end{pmatrix} $$

Verificamos que sean linealmente independientes:

$$ r_k \begin{pmatrix} 1 & 3 \\ -3 & -2 \\ -2 & -3 \end{pmatrix} = 2 $$

El rango (r_k = 2) coincide con el número de vectores (2).

Por lo tanto, los vectores son linealmente independientes y pueden utilizarse como base para el plano.

Elegimos el punto P₁ como punto de referencia P₀ en el plano:

$$ P_0 = P_1 $$

$$ \begin{pmatrix} x_0 \\ y_0 \\ z_0 \end{pmatrix} = \begin{pmatrix}1 \\ 3 \\ 5 \end{pmatrix} $$

Con esto, podemos escribir la ecuación vectorial del plano:

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = P_0 + t_1 \cdot v_1 + t_2 \cdot v_2 $$

$$ \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix}1 \\ 3 \\ 5 \end{pmatrix} + t_1 \cdot \begin{pmatrix} 1 \\ -3 \\ -2 \end{pmatrix} + t_2 \cdot \begin{pmatrix} 3 \\ -2 \\ -3 \end{pmatrix} $$

De aquí se obtiene la ecuación paramétrica del plano:

$$ \begin{cases} x = 1 + t_1 \cdot 1 + t_2 \cdot 3 \\ y = 3 + t_1 \cdot (-3) + t_2 \cdot (-2) \\ z = 5 + t_1 \cdot (-2) + t_2 \cdot (-3) \end{cases} $$

$$ \begin{cases} x = 1 + t_1 + 3 t_2 \\ y = 3 - 3 t_1 - 2 t_2 \\ z = 5 - 2 t_1 - 3 t_2 \end{cases} $$

Finalmente, deducimos la ecuación cartesiana del plano calculando el determinante de la matriz:

Trasladamos las coordenadas de P₀ al primer miembro:

$$ \begin{cases} x - 1 = t_1 + 3 t_2 \\ y - 3 = - 3 t_1 - 2 t_2 \\ z - 5 = - 2 t_1 - 3 t_2 \end{cases} $$

Se transforma el sistema en una matriz:

$$ \begin{pmatrix} x - 1 & 1 & 3 \\ y-3 & -3 & -2 \\ z-5 & -2 & -3 \end{pmatrix} $$

Calculamos el determinante de la matriz:

$$ det \begin{pmatrix} x - 1 & 1 & 3 \\ y-3 & -3 & -2 \\ z-5 & -2 & -3 \end{pmatrix} $$

$$ ( x-1 ) \cdot \begin{vmatrix} -3 & -2 \\ -2 & -3 \end{vmatrix} - (y-3) \cdot \begin{vmatrix} 1 & 3 \\ -2 & -3 \end{vmatrix} +(z-5) \cdot \begin{vmatrix} 1 & 3 \\ -3 & -2 \end{vmatrix} $$

$$ ( x-1 ) \cdot 5 - (y-3) \cdot 3 +(z-5) \cdot 7 $$

$$ 5x - 5 - 3y + 9 + 7z - 35 $$

$$ 5x - 3y + 7z - 31 $$

Igualamos la ecuación a cero y obtenemos la ecuación cartesiana del plano:

$$ 5x - 3y + 7z - 31 = 0 $$

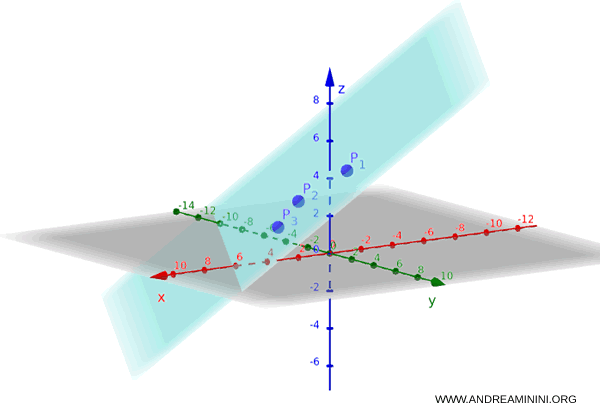
La representación gráfica del plano en el espacio tridimensional se muestra a continuación:

Y así sucesivamente.