Planos Perpendiculares
Dos planos que se intersecan se denominan planos perpendiculares cuando forman un ángulo diedro recto (90°).
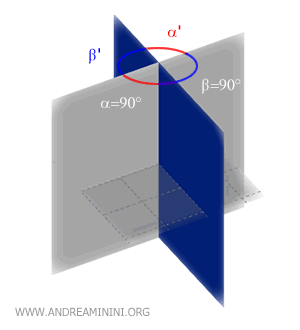
En otras palabras, el ángulo entre dos planos perpendiculares es de 90°.
De este modo, dos planos perpendiculares dividen el espacio en cuatro regiones diedras rectas.
También se conocen como planos normales u ortogonales.
Los planos perpendiculares se diferencian de los planos oblicuos. Los planos se consideran oblicuos cuando se intersecan, pero sin formar un ángulo diedro recto; es decir, su ángulo diedro es distinto de 90°.
Cuando dos planos forman un ángulo diedro recto, generan en realidad otros tres ángulos diedros rectos, ya que los diedros opuestos son congruentes.
Por ello, puede afirmarse que dos planos perpendiculares dividen el espacio tridimensional en cuatro diedros rectos, cada uno con un ángulo diedro de 90°.
Condiciones para Planos Perpendiculares
Veamos cómo determinar si dos planos son perpendiculares.
Al igual que sucede con las rectas, la perpendicularidad entre planos se basa en su orientación relativa: dos planos son perpendiculares si el ángulo entre ellos es exactamente de 90°.
Dados dos planos con las siguientes ecuaciones generales:
$$\pi_1: \ a x + b y + c z + d = 0 $$ $$ \pi_2: \ a' x + b' y + c' z + d' = 0 $$ los planos son perpendiculares si, y solo si, el producto escalar de sus vectores normales es igual a cero:
$$a \cdot a' + b \cdot b' + c \cdot c' = 0 $$
Cada plano se define mediante un vector normal, perpendicular al propio plano:
$$ \vec{n_1} = (a, b, c) $$
$$ \vec{n_2} = (a', b', c') $$
El ángulo entre los dos planos coincide con el ángulo entre sus vectores normales.
Por tanto, si el producto escalar de los vectores normales es cero, estos son ortogonales, lo que implica que los planos también lo son.
Ejemplo
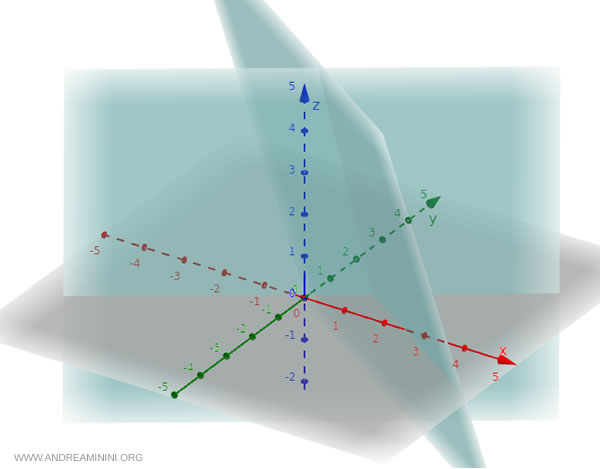
Consideremos los siguientes dos planos en forma general:
$$ \pi_1: \ 2x + 3y + z - 5 = 0 $$
$$ \pi_2: \ 4x - 6y - 2z + 1 = 0 $$
Calculemos ahora el producto escalar de sus vectores normales:
$$a \cdot a' + b \cdot b' + c \cdot c' $$
$$ (2, 3, 1) \cdot (4, -6, -2) = 2 \cdot 4 + 3 \cdot (-6) + 1 \cdot (-2) = 8 - 18 - 2 = -12 $$
Como el producto escalar no es cero, los dos planos no son perpendiculares.
Casos de Ecuaciones Explícitas
Cuando los planos se expresan en forma explícita:
$$ \pi_1: \ z = m x + n y + q $$ $$ \pi_2: \ z = m' x + n' y + q' $$ la condición de perpendicularidad es:
$$ m \cdot m' + n \cdot n' = -1 $$
Esta relación es muy parecida a la condición de perpendicularidad entre rectas en el plano $ xy $.
En este contexto, los coeficientes $ m $ y $ n $ representan las “pendientes” del plano respecto a los ejes $ x $ y $ y $.
Ejemplo
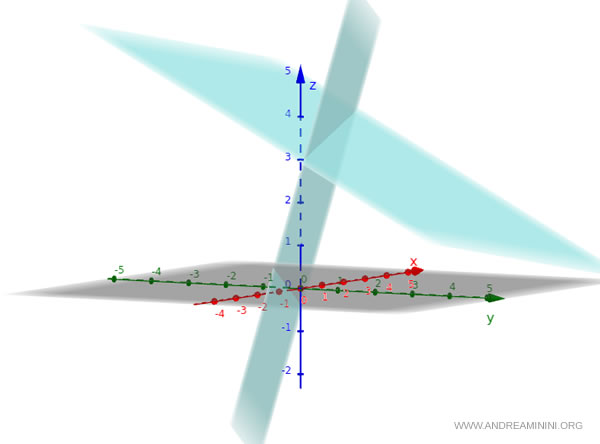
Consideremos los siguientes dos planos en forma explícita:
$$ \pi_1: \ z = 2x + 3y + 1 $$
$$ \pi_2: \ z = -\frac{1}{2}x - \frac{1}{3}y + 4 $$
Queremos verificar si estos dos planos son perpendiculares.
Cuando las ecuaciones están en la forma $ z = m x + n y + q $, la condición de perpendicularidad es:
$$ m \cdot m' + n \cdot n' = -1 $$
Para el primer plano, $ m = 2 $ y $ n = 3 $; para el segundo plano, $ m' = -\frac{1}{2} $ y $ n' = -\frac{1}{3} $.
$$ m \cdot m' + n \cdot n' = 2 \cdot \left( -\frac{1}{2} \right) + 3 \cdot \left( -\frac{1}{3} \right) = -1 + (-1) = -2 $$
Como el resultado no es igual a -1,
$$ m \cdot m' + n \cdot n' = -2 \neq -1 $$
los planos no son perpendiculares.
Si hubiéramos obtenido:
$$ m \cdot m' + n \cdot n' = -1 $$ entonces los planos sí serían perpendiculares.
Y así sucesivamente.