Distancia entre una Recta y un Plano Paralelo

La distancia $ d $ entre una recta $ r $ y un plano paralelo $ \pi $ se determina eligiendo un punto $ P $ sobre la recta y proyectándolo perpendicularmente sobre el plano.
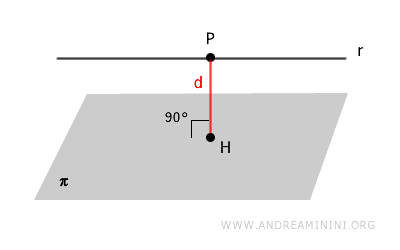
ejemplo

La fórmula para calcular la distancia $ d $ desde un punto $ P(x_0, y_0, z_0) $ hasta un plano definido por la ecuación $ ax + by + cz + d = 0 $ es:

$$ d = \frac{|ax_0 + by_0 + cz_0 + d|}{\sqrt{a^2 + b^2 + c^2}} $$

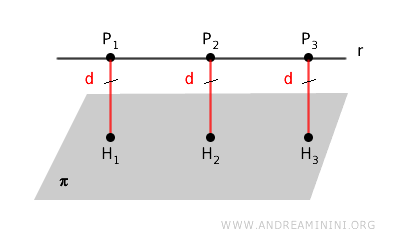
Esta expresión nos da la longitud del segmento perpendicular que une el punto $ P $ con el plano $ \pi $. Dado que la recta $ r $ es paralela al plano, dicha distancia es constante para cualquier punto situado sobre la recta.

ejemplo

Ejemplo

Consideremos el plano $ \pi $, cuya ecuación es:

$$ 2x - 3y + 6z + 9 = 0 $$

Supongamos que la recta $ r $ está definida mediante las ecuaciones paramétricas:

$$ x = 13 + 3t $$

$$ y = 2t $$

$$ z = 0 $$

Para verificar que la recta $ r $ es paralela al plano $ \pi $, calculamos el producto escalar entre el vector normal del plano $ (2, -3, 6) $ y el vector director de la recta $ (3, 2, 0) $:

$$ 2 \cdot 3 + (-3) \cdot 2 + 6 \cdot 0 = 6 - 6 + 0 = 0 $$

Como el producto escalar resulta cero, se confirma que la recta y el plano son efectivamente paralelos.

Escogemos ahora un punto cualquiera sobre la recta $ r $. Para $ t = 0 $, el punto es $ (13, 0, 0) $. Aplicamos entonces la fórmula de la distancia:

$$ d = \frac{|2(13) - 3(0) + 6(0) + 9|}{\sqrt{2^2 + (-3)^2 + 6^2}} $$

$$ d = \frac{|26 + 9|}{\sqrt{4 + 9 + 36}} $$

$$ d = \frac{35}{\sqrt{49}} $$

$$ d = \frac{35}{7} = 5 $$

Por lo tanto, la distancia entre la recta $ r $ y el plano $ \pi $ es igual a 5.

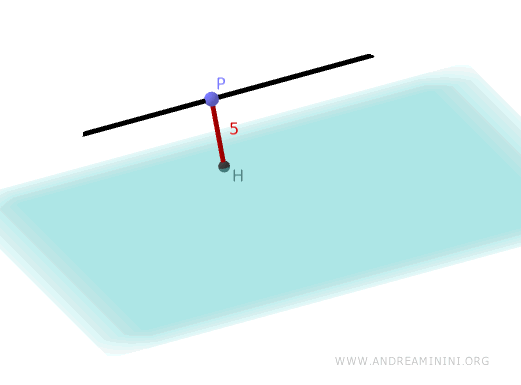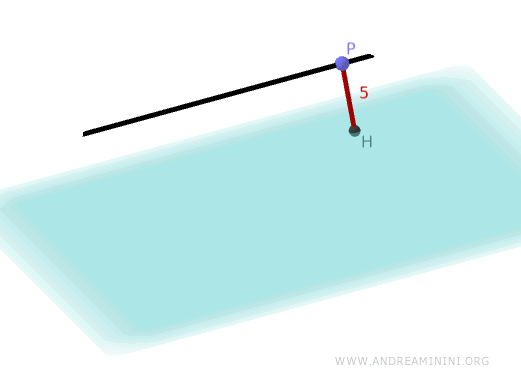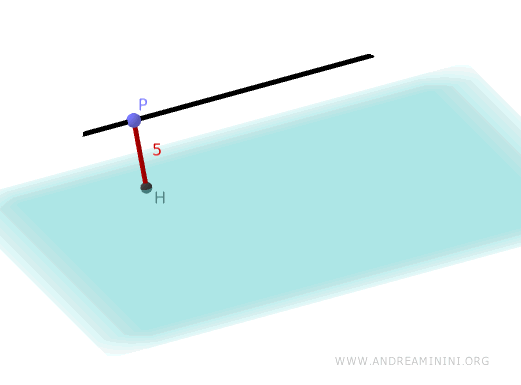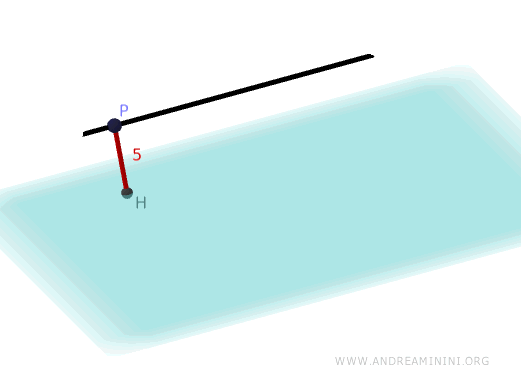
distancia entre una recta y un plano

Y así sucesivamente.