Planos Paralelos

Se dice que dos planos en el espacio son paralelos si cumplen alguna de estas condiciones:

• No tienen ningún punto en común, es decir, nunca se intersectan. A estos se les denomina planos paralelos no coincidentes.
• Coinciden en todos sus puntos, es decir, son exactamente el mismo plano. En ese caso, se llaman planos coincidentes.

Por ejemplo, los suelos de dos plantas en un edificio, siempre que sean perfectamente horizontales, constituyen un par de planos paralelos no coincidentes.

Distancia entre Planos Paralelos

La distancia entre dos planos paralelos no coincidentes es la longitud del segmento perpendicular que une un punto de un plano con otro punto situado en el otro plano.

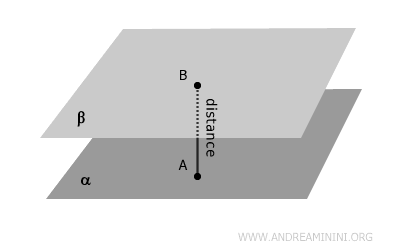
Dicha distancia es constante, sin importar el punto elegido en ambos planos.

Cálculo de la Distancia entre Dos Planos Paralelos

En geometría analítica, las ecuaciones de dos planos paralelos suelen expresarse así:

$$ Ax + By + Cz + D_1 = 0 $$

$$ Ax + By + Cz + D_2 = 0 $$

La distancia entre estos dos planos se obtiene mediante la fórmula:

$$ d = \frac{|D_2 - D_1|}{\sqrt{A^2 + B^2 + C^2}} $$

donde \( A, B, C \) son los coeficientes del vector normal a los planos.

Nota: Si la distancia es cero \( d=0 \), los planos son coincidentes. Si es un valor positivo \( d>0 \), se trata de dos planos distintos pero paralelos.

Ejemplo

Consideremos los siguientes dos planos paralelos:

$$ 2x + 3y + 6z + 4 = 0 $$

$$ 2x + 3y + 6z - 8 = 0 $$

Aplicando la fórmula:

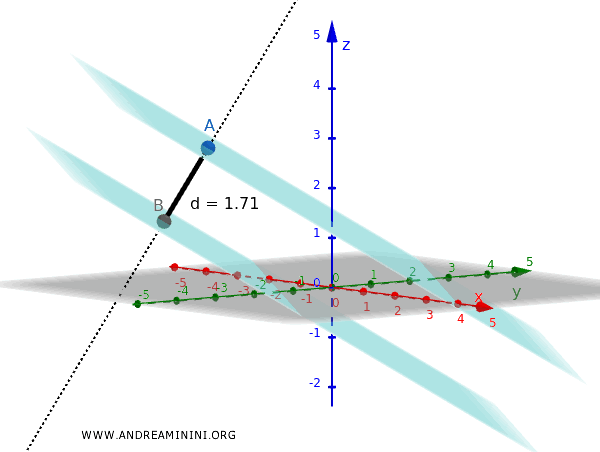
$$ d = \frac{| -8 - 4 |}{\sqrt{2^2 + 3^2 + 6^2}} = \frac{12}{\sqrt{4+9+36}} = \frac{12}{\sqrt{49}} = \frac{12}{7} \approx 1.71 $$

Por tanto, la distancia entre ambos planos es, aproximadamente, 1,71 unidades.

Propiedades de los Planos Paralelos

El paralelismo entre planos cumple ciertas propiedades fundamentales:

• Propiedad reflexiva: Todo plano es paralelo a sí mismo. $$ \alpha \parallel \alpha $$
• Propiedad simétrica: Si un plano \(\alpha\) es paralelo a otro plano \(\beta\), entonces \(\beta\) es paralelo a \(\alpha\). $$ \alpha \parallel \beta \quad \Rightarrow \quad \beta \parallel \alpha $$
• Propiedad transitiva: Si un plano \(\alpha\) es paralelo a un plano \(\beta\) y \(\beta\) es paralelo a un plano \(\gamma\), entonces \(\alpha\) es paralelo a \(\gamma\). $$ \alpha \parallel \beta, \quad \beta \parallel \gamma \quad \Rightarrow \quad \alpha \parallel \gamma $$

Estas tres propiedades permiten establecer que el paralelismo entre planos constituye una relación de equivalencia en geometría.

Condición para que Dos Planos Sean Paralelos

Dadas las ecuaciones generales de dos planos: $$ ax+by+cz+d = 0 $$ $$ a'x+b'y+c'z+d' = 0 $$ los planos son paralelos si $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} $$. En particular, son idénticos si $$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = \frac{d}{d'} $$

Analicemos dos planos definidos por estas ecuaciones generales:

$$ ax + by + cz + d = 0 $$

$$ a'x + b'y + c'z + d' = 0 $$

Los coeficientes $ a, b, c $ y $ a', b', c' $ representan las componentes de los vectores normales a ambos planos:

$$ \vec{n} = (a, b, c), \quad \vec{n'} = (a', b', c') $$

Dos planos son paralelos si, y solo si, sus vectores normales son proporcionales; es decir, existe un número real $ k $ tal que:

$$ \vec{n} = k \, \vec{n'} \quad \text{o, lo que es equivalente,} \quad (a, b, c) = k \, (a', b', c') $$

En otras palabras, esto implica:

$$
\begin{cases}
a = k a' \\
b = k b' \\
c = k c'
\end{cases}
$$

Dicho de forma sencilla, las razones entre los coeficientes correspondientes deben ser iguales:

$$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = k $$

Es decir, $ a, b, c $ han de ser proporcionales, respectivamente, a $ a', b', c' $.

Condición para que Dos Planos Coincidan

Dos planos:

$$ a x + b y + c z + d = 0 $$

$$ a' x + b' y + c' z + d' = 0 $$

son coincidentes si existe un número real $ k \neq 0 $ tal que:

$$ (a, b, c, d) = k \cdot (a', b', c', d') $$

Es decir, todos los coeficientes, incluido el término independiente, han de ser proporcionales.

En la práctica, esta condición se verifica comprobando:

$$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = \frac{d}{d'} = k $$

siempre que ninguno de los denominadores sea cero.

Nota. Si alguno de los denominadores es cero, los numeradores correspondientes también deben ser cero, y los coeficientes restantes han de seguir cumpliendo la condición de proporcionalidad. Por ejemplo, si $ d' = 0 $, entonces también debe cumplirse que $ d = 0 $, y viceversa.

Ejemplo

Consideremos estos dos planos:

$$ 3x + 6y - 9z + 12 = 0 $$

$$ x + 2y - 3z + 4 = 0 $$

Calculemos las razones de los coeficientes correspondientes:

$$ \frac{3}{1} = 3, \quad \frac{6}{2} = 3, \quad \frac{-9}{-3} = 3 $$

Como todas estas razones coinciden:

$$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = 3 $$

podemos concluir que los vectores normales son proporcionales, lo que indica que los planos son paralelos.

Nota. Los coeficientes representan las componentes de los vectores normales a los planos: $$ \vec{n} = (3, 6, -9), \quad \vec{n'} = (1, 2, -3) $$ Un “vector normal” es un vector perpendicular al plano. Aquí tienes un ejemplo de vector normal:

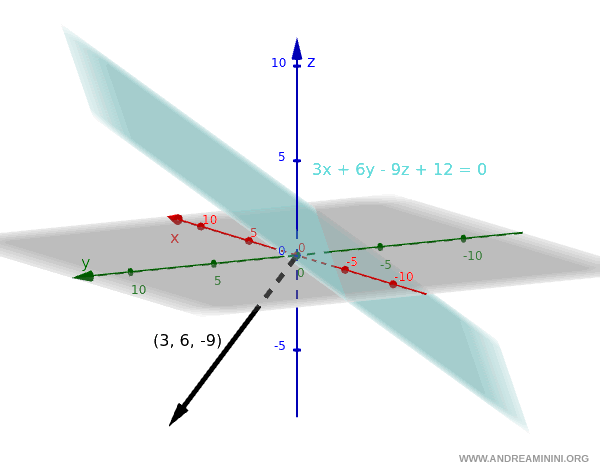
Ahora comprobemos los términos independientes:

$$ \frac{12}{4} = 3 $$

Nuevamente, esta razón es 3. Por tanto:

$$ \frac{a}{a'} = \frac{b}{b'} = \frac{c}{c'} = \frac{d}{d'} = 3 $$

Esto demuestra que los dos planos no solo son paralelos, sino que, en realidad, son idénticos.

Notas Adicionales

He aquí algunas observaciones adicionales sobre los planos paralelos:

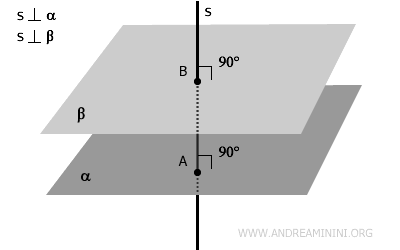
• Si dos planos son paralelos, cualquier recta perpendicular a uno de ellos también lo será al otro.
  
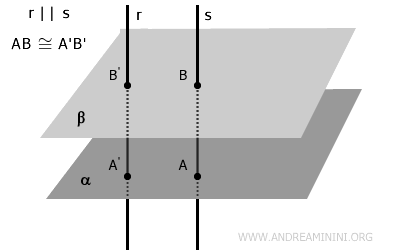
• Si dos planos paralelos son interceptados por dos rectas paralelas - ya sea perpendiculares o inclinadas - , los segmentos comprendidos entre ambos planos en dichas rectas son congruentes. $$ AB \cong A'B' $$.
  

Y así sucesivamente.