Ángulo entre una Recta y un Plano
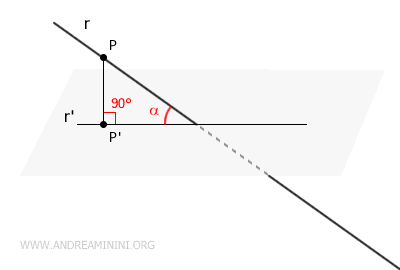
El ángulo entre una recta (r) y un plano se define como el ángulo α formado entre la propia recta y su proyección ortogonal (r') sobre dicho plano.
Una misma recta puede formar distintos ángulos con un plano, dependiendo de cómo se considere su proyección.
Esto se debe a que existen infinitos planos que pueden cortar a una misma recta.
No obstante, no todos estos ángulos tienen la misma importancia desde el punto de vista geométrico.
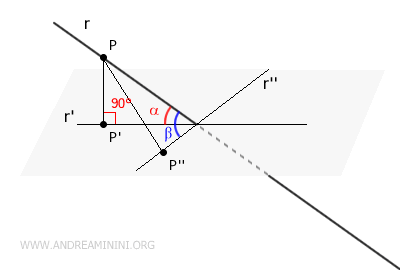
El ángulo que, por convención, se considera como el ángulo entre la recta y el plano es el ángulo mínimo.
Dicho ángulo se obtiene cuando la proyección de la recta sobre el plano es perpendicular (90°) al propio plano.
Un Ejemplo Práctico
Imaginemos en este caso una recta r y un plano α.
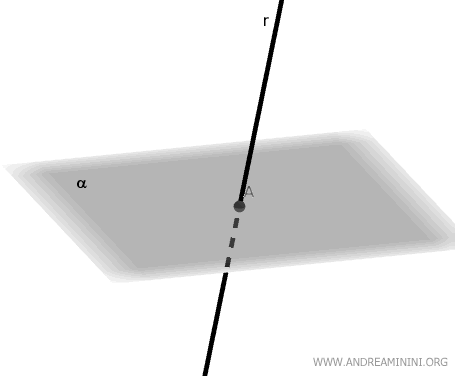
Si consideramos un plano β (distinto del plano α) que corta a la recta r, la proyección r' de la recta r sobre el plano α forma un ángulo de 93,5°.

Sin embargo, si elegimos otro plano β' que también pase por la recta r, el ángulo entre la recta r y el plano α será diferente.
Por ejemplo, en este caso, el ángulo entre la recta y el plano α es de 99,71°.
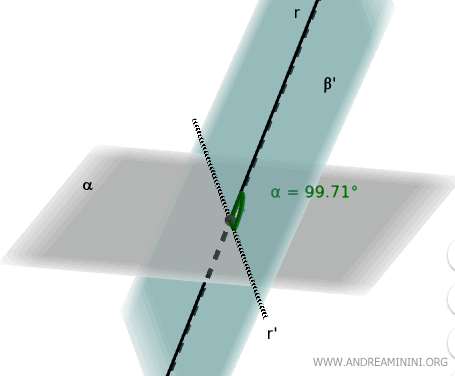
Nota: El plano α y la recta r permanecen inalterados. Lo único que varía es el plano β que se considera, el cual pasa por la recta r y genera una proyección r' distinta sobre el plano α. Por eso, el ángulo entre la recta r y su proyección r' también cambia.
Para determinar el ángulo mínimo, debemos elegir un plano β'' que pase por la recta r y sea, además, un plano perpendicular (90°) al plano α.
En este caso, la proyección r' de la recta r sobre el plano α formaría un ángulo de 64,76°, que es el ángulo más pequeño posible.
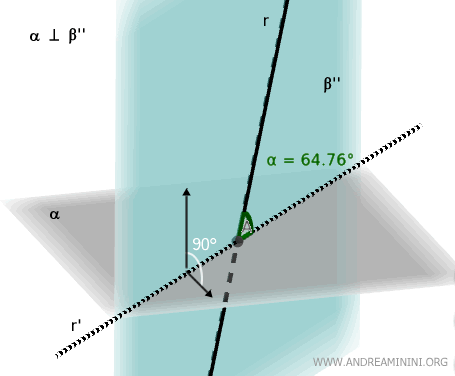
En conclusión, el ángulo entre una recta y un plano se define como el ángulo comprendido entre la recta y su proyección ortogonal sobre el plano, y corresponde siempre al ángulo de menor medida posible.
Y así sucesivamente.