Teorema de la recta perpendicular a dos planos

Si una recta $ r $ es perpendicular a dos planos $ \alpha $ y $ \beta $ en los puntos $ P $ y $ Q $, respectivamente (siendo $ P $ y $ Q $ puntos distintos sobre la recta), entonces los planos $ \alpha $ y $ \beta $ son paralelos, es decir, $ \alpha \parallel \beta $.
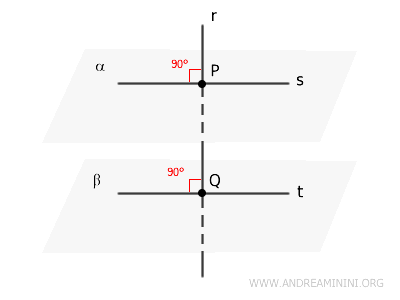
ilustración de la demostración

Este teorema, propio de la geometría espacial, constituye una herramienta esencial para analizar las relaciones entre rectas y planos en el espacio tridimensional.

Demostración

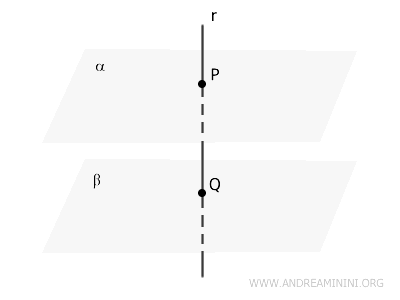
Sea $ r $ una recta que intersecta a los planos $ \alpha $ y $ \beta $ en los puntos $ P $ y $ Q $, respectivamente.

Por hipótesis, $ r $ es perpendicular tanto al plano $ \alpha $ como al plano $ \beta $.

ejemplo de una recta perpendicular a un plano

Esto significa que $ r $ forma ángulos rectos con cualquier recta contenida en $ \alpha $ que pase por $ P $, así como con cualquier recta contenida en $ \beta $ que pase por $ Q $.

Consideremos ahora una recta $ s $, contenida en $ \alpha $ y que pasa por $ P $, y una recta $ t $, contenida en $ \beta $ y que pasa por $ Q $.

ilustración de la demostración

Dado que $ r $ es perpendicular al plano $ \alpha $, necesariamente es perpendicular a $ s $.

De forma análoga, $ r $ es perpendicular a $ t $.

Supongamos ahora, por reducción al absurdo, que los planos $ \alpha $ y $ \beta $ no son paralelos.

Si $ \alpha $ y $ \beta $ no fueran paralelos, se cortarían en una recta $ u $. Esto implicaría que $ u $ pertenece simultáneamente a $ \alpha $ y a $ \beta $.

Dado que $ r $ es perpendicular a todas las rectas de $ \alpha $ que pasan por $ P $, también lo sería a $ u $, pues $ u $ se halla contenido en $ \alpha $.

$$ u \subset \alpha $$

De igual modo, como $ r $ es perpendicular a todas las rectas de $ \beta $ que pasan por $ Q $, también lo sería a $ u $, ya que $ u $ está contenida en $ \beta $.

$$ u \subset \beta $$

Sin embargo, es imposible que una misma recta $ r $ sea perpendicular a la misma recta $ u $ en dos puntos distintos $ P $ y $ Q $, pues ello vulnera la unicidad de la perpendicular trazada desde un punto a una recta.

Por tanto, la hipótesis de que $ \alpha $ y $ \beta $ no son paralelos resulta insostenible.

En consecuencia, se concluye que los planos $ \alpha $ y $ \beta $ deben ser paralelos.

Demostración alternativa

Consideremos una recta $ r $ perpendicular al plano $ \alpha $ en el punto $ P $.

Dado que $ r $ es perpendicular a $ \alpha $ en $ P $, el vector director de $ r $, que denotamos $ \vec{v} $, es un vector normal (ortogonal) al plano $ \alpha $.

Esto implica que $ \vec{v} $ es perpendicular a cualquier vector contenido en $ \alpha $.

Del mismo modo, como $ r $ es perpendicular al plano $ \beta $ en el punto $ Q $, el vector $ \vec{v} $ es también un vector normal al plano $ \beta $.

En consecuencia, $ \vec{v} $ actúa como vector normal común a ambos planos, lo que implica que $ \alpha $ y $ \beta $ comparten la misma dirección normal. Esto significa que sus vectores normales son paralelos.

Cuando dos planos poseen vectores normales paralelos, necesariamente son planos paralelos. Por tanto, $ \alpha $ y $ \beta $ son paralelos.

Con esto, queda rigurosamente demostrado el teorema.