Recta perpendicular a un plano

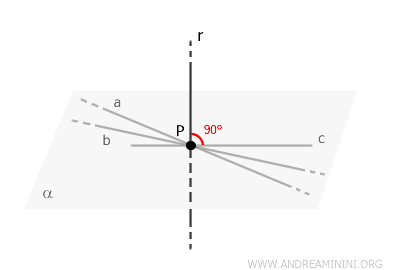
Se dice que una recta \( r \) es perpendicular a un plano \( \alpha \) si lo corta y es perpendicular a todas las rectas contenidas en dicho plano.

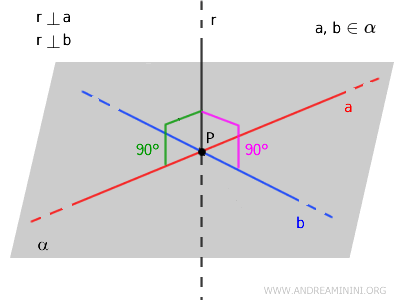
Para que una recta \( r \) sea perpendicular a un plano \( \alpha \), deben cumplirse dos condiciones:

• La recta \( r \) corta al plano \( \alpha \) en un único punto \( P \), que pertenece al plano.
• La recta \( r \) es perpendicular a todas las rectas del plano \( \alpha \) que pasan por el punto de intersección \( P \).

Nota: Una recta que corta al plano en un solo punto, pero que no es perpendicular, se denomina recta oblicua al plano.

Observaciones adicionales

A continuación, se presentan algunas consideraciones y resultados relevantes sobre la perpendicularidad entre rectas y planos.

• Teorema de las tres perpendiculares
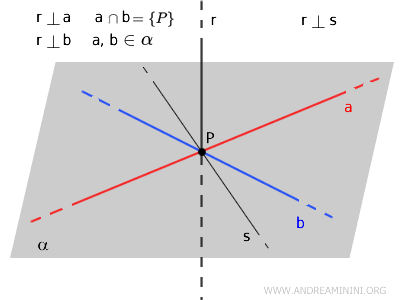
  Si desde un punto \( P \) sobre la recta \( r \) se trazan dos rectas \( a \) y \( b \), ambas perpendiculares a \( r \), entonces \( r \) resulta perpendicular a cualquier otra recta \( s \) que pase por \( P \) y se encuentre en el plano \( \alpha \) definido por \( a \) y \( b \).
  
• Teorema de las rectas perpendiculares a una recta en el espacio
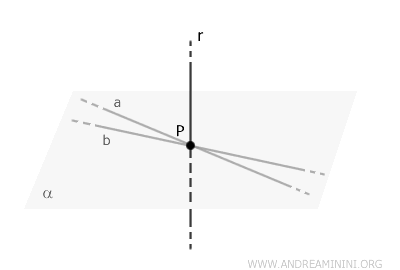
  En el espacio, toda recta perpendicular a una recta dada \( r \) y que pase por un punto \( P \) situado sobre \( r \) ha de encontrarse en un mismo plano.
  
• Teorema de las tres perpendiculares
  Sea una recta \( r \) perpendicular a un plano \( \alpha \). Si desde el pie de la perpendicular \( H \) se traza una recta \( t \), de manera que \( t \) es perpendicular a otra recta \( s \) contenida en el plano \( \alpha \), entonces \( s \) es también perpendicular al plano \( \beta \), definido por las rectas \( r \) y \( t \).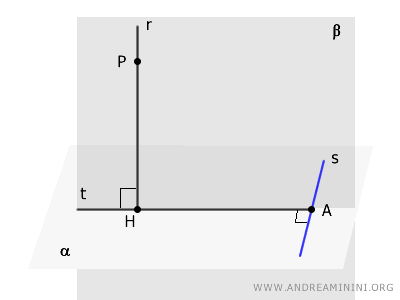

  

• Teorema de la recta perpendicular a un plano
  Por cualquier punto \( P \) perteneciente al plano \( \alpha \) pasa exactamente una única recta \( r \) perpendicular a dicho plano.
  
• Teorema de las rectas perpendiculares
  Dos rectas perpendiculares a un mismo plano son paralelas entre sí.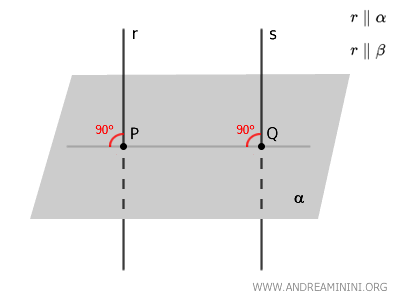

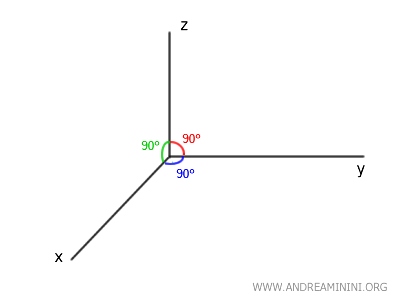
  Nota: En el espacio tridimensional, el teorema que establece que dos rectas perpendiculares a una misma recta son paralelas no es válido. Dicho resultado solo se cumple en un plano (2D). Por ejemplo, los ejes \(x\), \(y\) y \(z\) del sistema de coordenadas cartesianas son mutuamente perpendiculares ($ x \perp y $, $ x \perp z $, $ y \perp z $), pero no son paralelos entre sí.
  

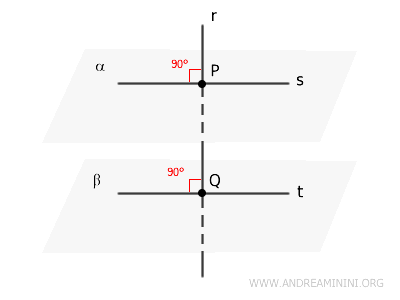
• Teorema de la recta perpendicular a dos planos
  Si una recta es perpendicular a dos planos en dos puntos distintos a lo largo de su recorrido, dichos planos necesariamente son paralelos.
  

Y así sucesivamente.