Teorema de la recta perpendicular a un plano
Dado un plano \( \alpha \) y un punto \( P \), existe una única recta \( r \) que pasa por \( P \) y es perpendicular al plano \( \alpha \).
Todo plano en el espacio posee una dirección perpendicular bien definida, determinada por su vector normal.
La recta \( r \) pasa por el punto \( P \) y está orientada en la misma dirección que el vector normal al plano \( \alpha \).
Nota: La unicidad de esta recta se fundamenta en el hecho de que el vector normal es único (salvo múltiplos escalares), lo cual garantiza que solo exista una recta con esta propiedad.
Demostración
Consideremos el plano \( \alpha \) y tomemos un punto arbitrario \( P \) situado en él.

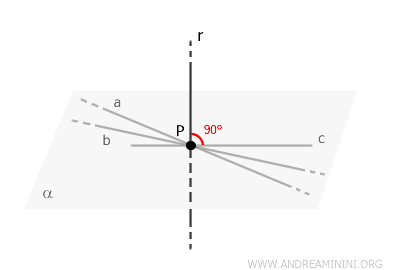
Un plano contiene infinitos puntos y, por ende, una infinidad de rectas coplanarias \( a \), \( b \), \( c \), y así sucesivamente.
Por definición, una recta es perpendicular al plano \( \alpha \) si forma un ángulo recto con toda recta trazada por \( P \) y contenida en el plano \( \alpha \).
Por lo tanto, dado el punto \( P \), siempre es posible determinar una recta \( r \), perpendicular al plano, que parte de \( P \) y forma ángulos rectos con todas las rectas contenidas en \( \alpha \).

Ahora debemos demostrar que dicha recta perpendicular \( r \) es única, es decir, que no existe ninguna otra recta distinta que posea esta misma propiedad.
Supongamos, para llegar a una contradicción, que existen dos rectas distintas \( r \) y \( r' \), ambas perpendiculares al plano \( \alpha \) y que pasan por el punto \( P \).

Si esto fuera cierto, al menos una de las dos rectas, \( r \) o \( r' \), no formaría un ángulo recto con alguna de las rectas contenidas en el plano \( \alpha \). De lo contrario, \( r \) y \( r' \) coincidirían, lo que contradiría la hipótesis de que son distintas.
Esta contradicción demuestra que no pueden existir dos rectas diferentes \( r \) y \( r' \) con la misma propiedad; en consecuencia, ambas deben ser la misma recta.
Por lo tanto, existe exactamente una única recta que pasa por \( P \) y es perpendicular al plano \( \alpha \).
Con esto, queda demostrada la proposición.