Ecuación de una Recta que Pasa por el Origen

La ecuación de una recta que pasa por el origen O(0,0) en el plano cartesiano es: $$ y = mx $$ 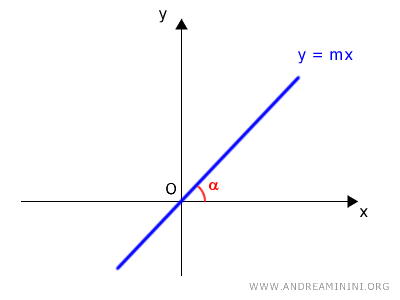ejemplo de una recta que pasa por el origen del plano

Esta ecuación tan simple se obtiene a partir de la forma explícita de la ecuación general de la recta.

$$ y = mx + c $$

En este caso, el término independiente o intercepto en el eje y es cero, es decir, $ c = 0 $.

$$ y = mx $$

Por lo tanto, el valor de $ y $ depende directamente de la pendiente (m) y del valor que se asigne a la variable $ x $.

$$ m = \frac{y}{x} $$

La pendiente $ m $ expresa la inclinación de la recta e indica el ángulo que forma con respecto al eje x.

Nota: La ecuación $ y = mx $ es, probablemente, la forma más sencilla e intuitiva de representar rectas que pasan por el origen, ya que refleja una relación lineal directa entre $ y $ y $ x $, sin desplazamiento vertical. Las variables $ x $ y $ y $ son directamente proporcionales, pues su razón permanece constante: $ m = \frac{y}{x} $.

La pendiente $ m $ puede asumir cualquier valor real.

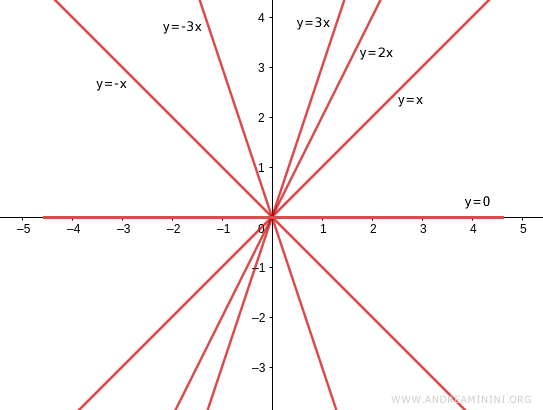
Si $ m > 0 $, la recta se inclina hacia arriba de izquierda a derecha. En este caso, el ángulo que forma con el eje x es agudo.
Si $ m < 0 $, la recta se inclina hacia abajo. En este caso, el ángulo que forma con el eje x es obtuso.
Si $ m = 0 $, la recta es horizontal y coincide con el eje x. Su ecuación es $ y = 0 $, y el ángulo con el eje x es cero.

familia de rectas que pasan por el origen

Además, si la pendiente $ m $ es indefinida, la recta es vertical y coincide con el eje y.

Para representar este caso particular, se emplea la ecuación $ x = 0 $.

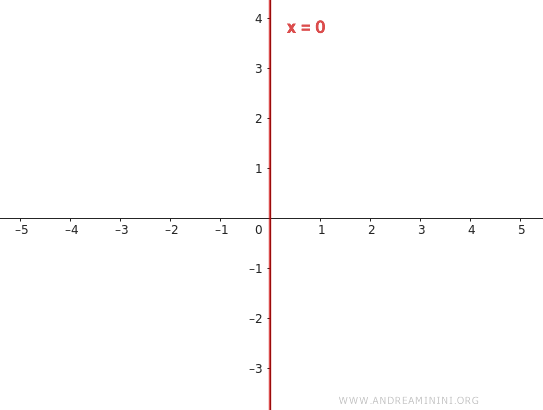
ecuación de la recta que pasa por el origen

Explicación: Cuando la pendiente $ m $ es indefinida o infinita, la recta ya no puede expresarse en la forma explícita $ y = mx $. Para describir una recta paralela al eje y, se utiliza la ecuación $ x = k $, donde $ k $ es una constante que indica la posición de la recta sobre el eje x. Si la recta pasa por el origen, dicha constante es cero, $ k = 0 $. Así, la ecuación de la recta se reduce a $ x = 0 $.

Existen, además, casos especiales de rectas que pasan por el origen, correspondientes a las pendientes $ m = 1 $ y $ m = -1 $.

Si m = 1, la recta coincide con la bisectriz del primer y tercer cuadrante. En este caso, la ecuación de la recta es $ y = x $.
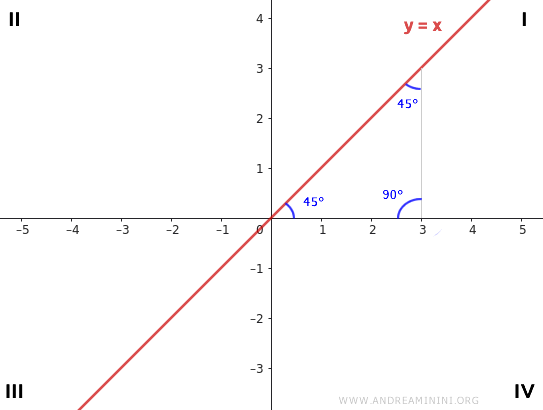
Si m = -1, la recta coincide con la bisectriz del segundo y cuarto cuadrante. En este caso, la ecuación de la recta es $ y = -x $.

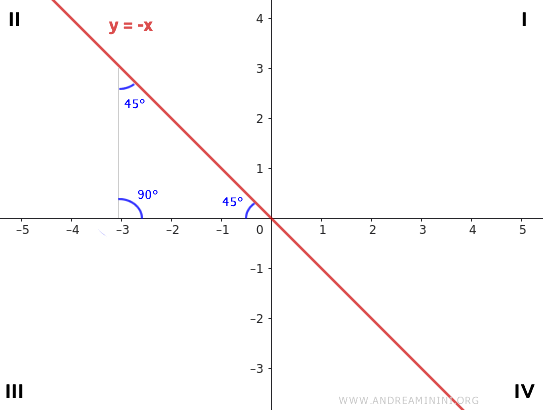
En ambos casos, $ m = 1 $ y $ m = -1 $, se forma un triángulo rectángulo isósceles, con un ángulo recto de 90° y dos ángulos de 45° cada uno.

Y así sucesivamente.