Teorema de la Perpendicular desde un Punto a una Recta
Por cualquier punto P en un plano pasa exactamente una única recta perpendicular a una recta dada “r”.
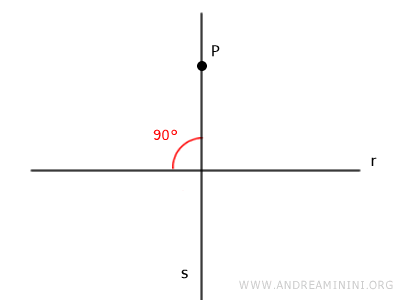
En términos prácticos, si elegimos un punto P cualquiera en el plano y una recta r que no necesariamente pase por él, existe una única recta s perpendicular a r que pasa por P.
Al punto donde la perpendicular corta a la recta r se le llama el pie de la perpendicular.
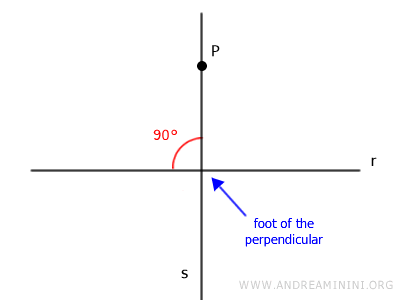
Este resultado también se conoce como teorema de existencia y unicidad de la perpendicular trazada desde un punto a una recta.
Demostración
Sea $ P $ un punto situado fuera de la recta $ r $ y sea $ s \perp r $ la recta perpendicular a $ r $ que pasa por $ P $.
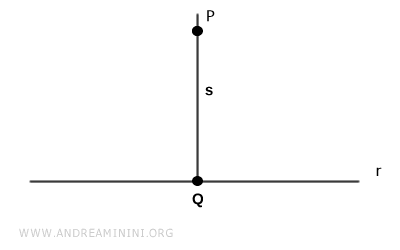
Denotemos por $ Q $ el pie de la perpendicular trazada desde $ P $ sobre $ r $.
Tomamos dos puntos distintos $ A $ y $ B $ sobre la recta $ r $ de modo que ambos queden a la misma distancia de $ Q $.
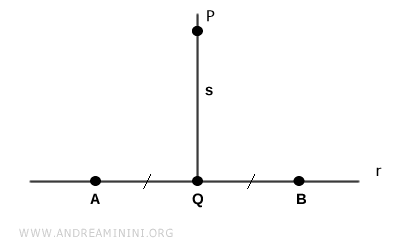
Se trazan los segmentos $ AP $ y $ BP $.
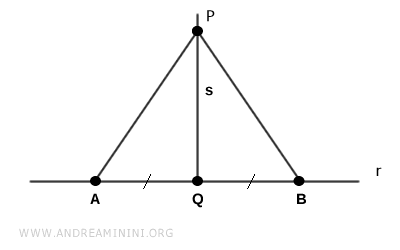
Por construcción, el segmento $ PQ $ es bisectriz del ángulo $ A \hat P B $. Dado que $ PQ $ se encuentra sobre $ s $, la bisectriz de dicho ángulo resulta perpendicular a $ r $.
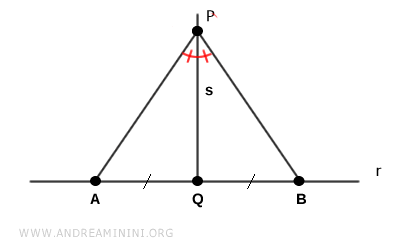
Y como la bisectriz de un ángulo es única, se concluye que la perpendicular $ s $ trazada desde el punto $ P $ a la recta $ r $ es única.
Otra Demostración
La demostración se divide en dos casos distintos.
Debemos diferenciar si el punto P pertenece a la recta “r” o no.
A] El punto P pertenece a la recta (P ∈ r)
Consideremos una recta r en el plano y un punto cualquiera P sobre ella.
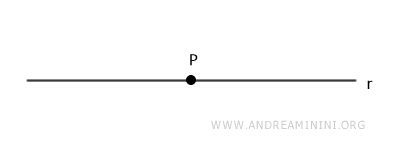
Con el compás centrado en P, marcamos dos puntos A y B sobre la recta con cualquier abertura.
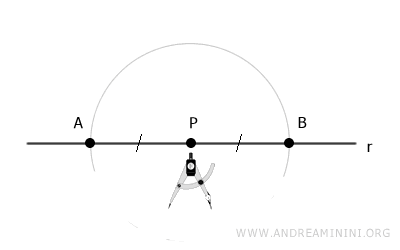
Los puntos A y B quedan a la misma distancia de P, por lo que los segmentos AP y BP son congruentes, es decir, tienen igual longitud.
$$ AP \cong BP $$
Así, el punto P es el punto medio del segmento AB.
Luego, centramos el compás en A y trazamos un arco de radio AB.
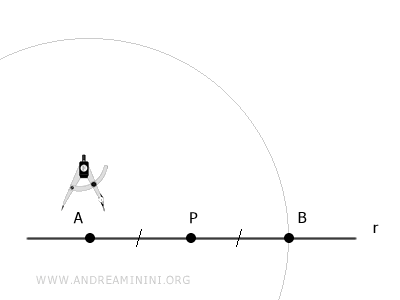
Después, centramos el compás en B y dibujamos otro arco con el mismo radio.
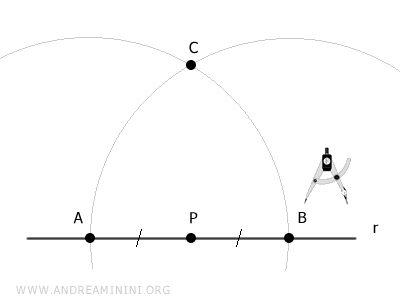
El punto donde se cruzan ambos arcos es el punto C.
Nota: Puede elegirse un radio distinto de AB, siempre que sea mayor que AP, para asegurar que los arcos se corten.
Dado que sólo existe una recta que pasa por dos puntos distintos en el plano,
existe exactamente una recta s que pasa por los puntos P y C.
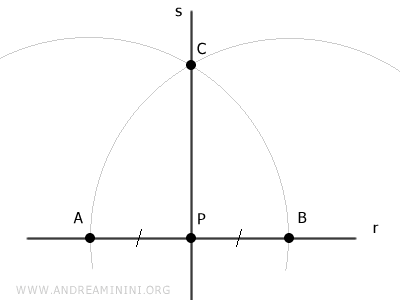
La recta s es perpendicular a la recta r porque, si consideramos el triángulo ABC, es un triángulo isósceles, ya que los lados AC y BC son congruentes por construcción (AC≅BC).
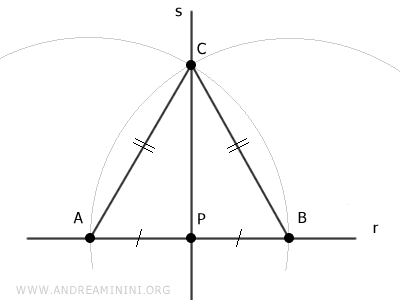
El segmento CP es la mediana de dicho triángulo porque une el vértice C con el punto medio P del lado opuesto AB.
Y dado que en un triángulo isósceles la mediana coincide con la altura, se deduce que el segmento CP forma un ángulo recto con la base AB.
Por tanto, la recta s, que contiene el segmento CP, es perpendicular a la recta r.
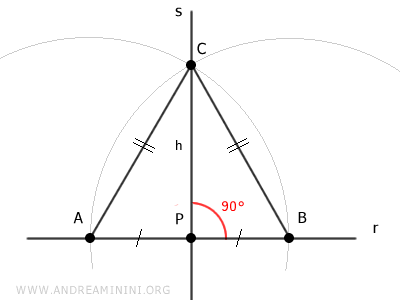
Con esto, queda demostrada tanto la existencia como la unicidad de la recta perpendicular.
Nota: La unicidad se demuestra porque sólo hay una recta que pasa por dos puntos distintos C y P. Además, el triángulo ABC es isósceles, y en los triángulos isósceles la mediana CP coincide también con la bisectriz del ángulo en el vértice C. Saber que un ángulo sólo tiene una bisectriz refuerza la unicidad de la recta s.
B] El punto P no pertenece a la recta (P ∉ r)
Consideremos una recta r y un punto P en el plano que no pertenece a dicha recta.
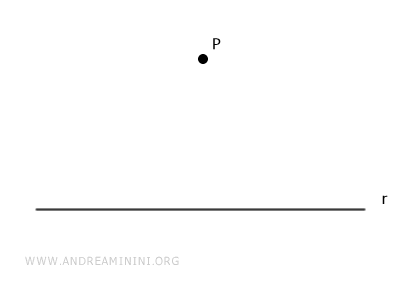
Elegimos cualquier punto A sobre la recta r y trazamos el segmento AP.
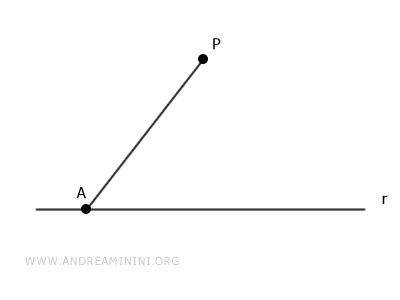
Centramos el compás en A y dibujamos un arco con radio AP.
El punto donde este arco corta a la recta r es el punto B.
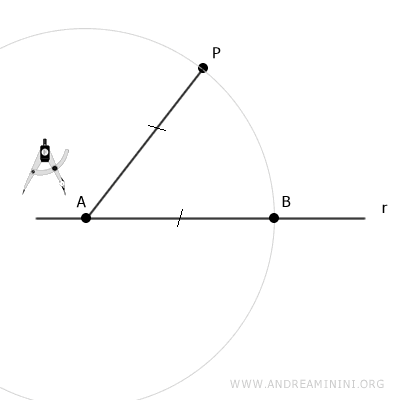
Por construcción, los segmentos AP y AB son congruentes.
$$ \overline{AP} \cong \overline{AB} $$
Luego, centramos el compás en B y trazamos otro arco con radio BP.
Los dos arcos se cruzan en los puntos P y C.
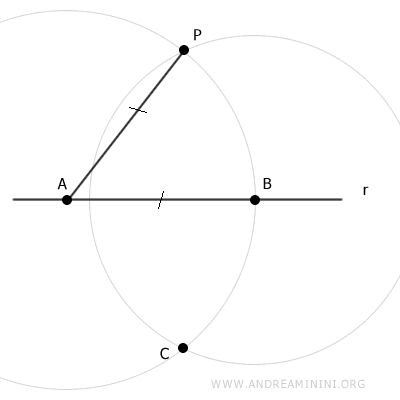
Se traza el segmento CP que une los puntos P y C.
El segmento CP corta a la recta r en el punto D.
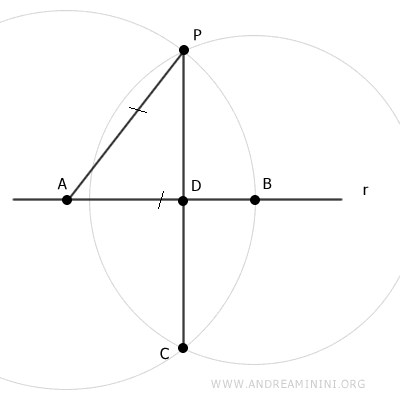
Se traza el segmento AC, que por construcción es congruente al segmento AP (AC≅AP).
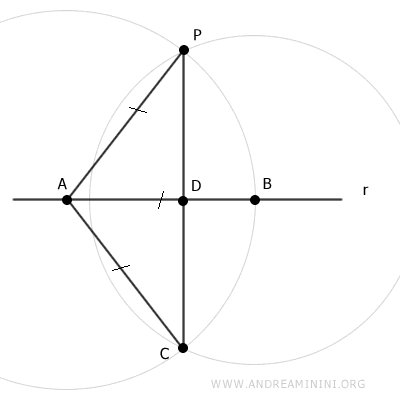
Asimismo, se trazan los segmentos BP y BC, también congruentes por construcción (BP≅BC).
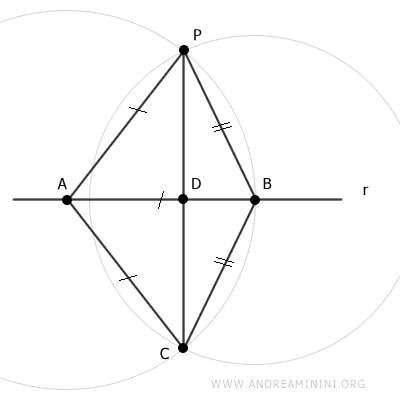
De acuerdo con el tercer criterio de congruencia de triángulos (Lado-Lado-Lado), los triángulos APB y ACB son congruentes porque comparten el lado AB y tienen otros dos lados congruentes: AP≅AC y BP≅BC.
$$ APB \cong ACB $$
Por tanto, los triángulos APB y ACB presentan ángulos congruentes en correspondencia.
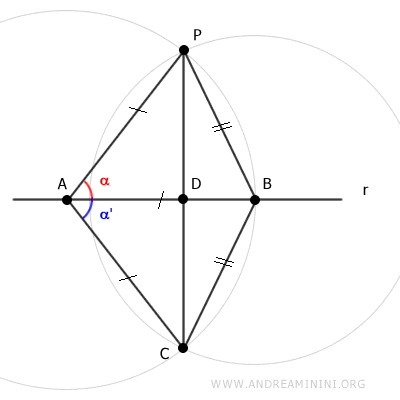
Nos interesa especialmente la congruencia entre los ángulos α y α'.
Esto permite concluir que los triángulos APD y ACD son congruentes, pues comparten un ángulo congruente (α≅α'), un lado congruente (AP≅AC) y el lado común AD.
$$ APD \cong ACD $$
En consecuencia, los segmentos PD y CD son congruentes (PD≅CD).
Por tanto, el punto D es el punto medio del segmento PC.
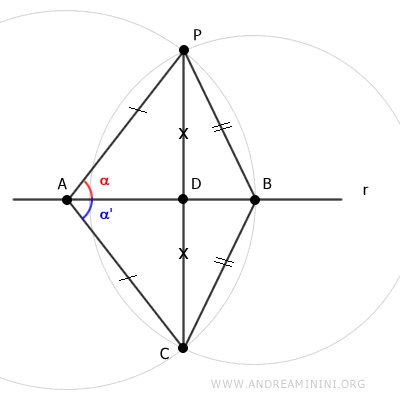
Consideremos ahora el triángulo APC, que es un triángulo isósceles porque tiene dos lados iguales, AP y AC.
El segmento AD es la mediana de este triángulo, ya que une el vértice A con el punto medio D del lado opuesto PC.
En un triángulo isósceles, la mediana coincide con la altura y también con la bisectriz del ángulo.
Nota: Por definición, la altura de un triángulo es el segmento que une un vértice con un punto del lado opuesto (o su prolongación) formando un ángulo recto.
Por ello, el segmento AD es perpendicular al segmento PC.
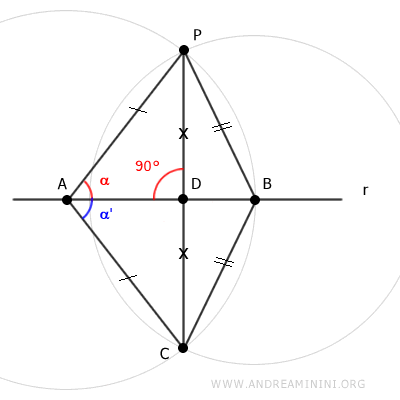
Así, dado que sólo existe una recta que pasa por dos puntos distintos, la recta s que pasa por los puntos P y C es perpendicular a la recta r que pasa por los puntos A y B.
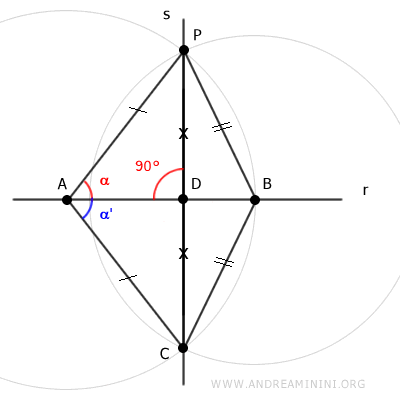
Nota: Además de que sólo existe una recta que pasa por dos puntos distintos, la unicidad se prueba también porque el triángulo APC es isósceles, y en los triángulos isósceles la mediana AD coincide con la bisectriz del ángulo en el vértice A. Por tanto, la recta r es perpendicular a la recta s y viceversa.
Queda así demostrado que existe exactamente una recta s perpendicular a la recta r que pasa por el punto C.
$$ r \perp s $$
Verificación: Si tomamos cualquier otro punto E sobre la recta r distinto del punto D, sabiendo que el segmento PD es perpendicular a r, los puntos PDE forman un triángulo rectángulo.
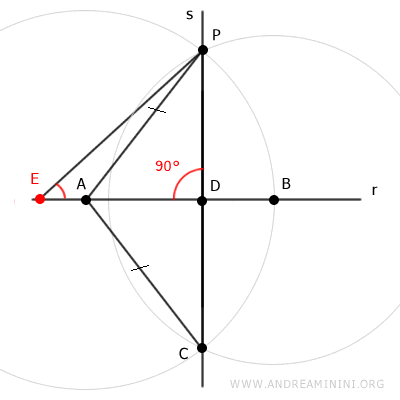
En un triángulo rectángulo, sólo puede existir un ángulo recto (de 90°). En este caso, ese ángulo recto está en el vértice D. Por tanto, los otros dos ángulos del triángulo PDE deben ser agudos (<90°). Esto implica que el segmento PE no puede ser perpendicular a la recta r. El mismo razonamiento se aplica a cualquier otro punto E sobre la recta r que no sea D.
Y así sucesivamente.