Tercer criterio de congruencia de triángulos
Dos triángulos son congruentes si sus tres lados son congruentes y se encuentran dispuestos en el mismo orden.
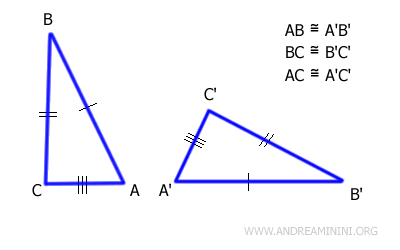
En otras palabras, dos triángulos se consideran congruentes cuando todos sus lados correspondientes tienen la misma longitud y siguen el mismo orden.
Este criterio también se conoce como LLL (Lado-Lado-Lado) o SSS (Side-Side-Side).
Consideremos, por ejemplo, los triángulos ABC y A'B'C'.
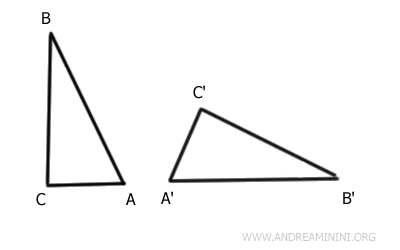
Aplicando una transformación rígida (traslación y rotación), el lado AB del primer triángulo coincide exactamente con el lado A'B' del segundo.
Por tanto, los lados AB y A'B' son congruentes.
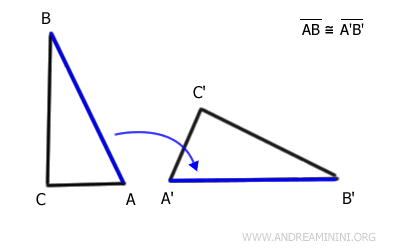
A continuación, consideramos los lados adyacentes BC y B'C'.
Tras otra transformación rígida, el lado BC del primer triángulo se superpone perfectamente con el lado B'C' del segundo.
Por tanto, BC y B'C' son congruentes.
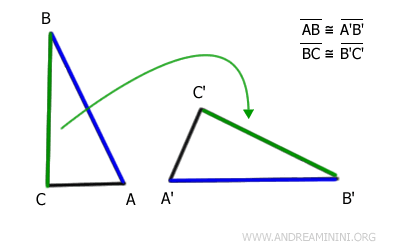
Finalmente, observamos los lados AC y A'C'.
Mediante una transformación adicional, el lado AC coincide exactamente con el lado A'C'.
Por tanto, AC y A'C' también son congruentes.
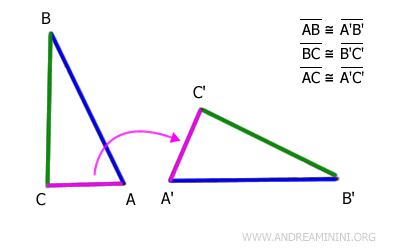
Así pues, todos los lados de ambos triángulos son congruentes y aparecen en el mismo orden.
Por lo tanto, los triángulos son congruentes.
Demostración
Este criterio es un teorema, ya que puede demostrarse rigurosamente.
Consideremos los triángulos ABC y A'B'C' del ejemplo anterior.
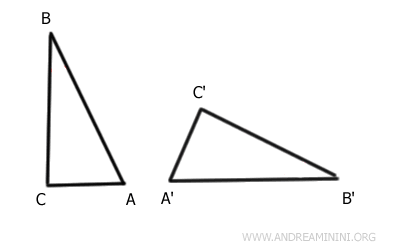
Sabemos que:
$$ \overline{AB} \cong \overline{A'B'} $$
$$ \overline{BC} \cong \overline{B'C'} $$
$$ \overline{AC} \cong \overline{A'C'} $$
Queremos demostrar que $ ABC \cong A'B'C' $.
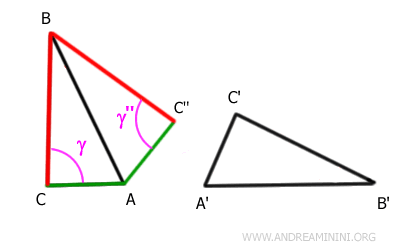
Aplicamos una transformación rígida (traslación, rotación y posible reflexión) para hacer coincidir los lados AB y A'B'.
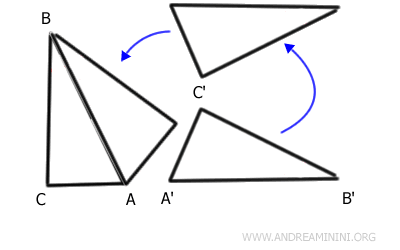
Designamos el nuevo vértice como C''.
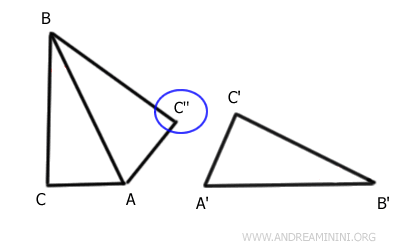
Por tanto, los triángulos AC''B y A'B'C' son congruentes.
$$ AC''B \cong A'B'C' $$
Ahora unimos los puntos C y C'' mediante el segmento $ \overline{CC''} $.
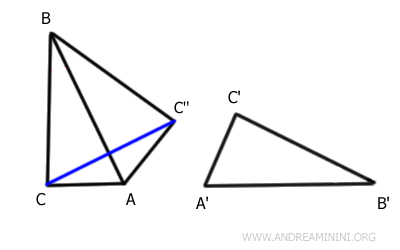
El triángulo AC''C es isósceles, con base $ \overline{CC''} $, ya que $ \overline{AC} \cong \overline{AC''} $.
Por lo que:
$$ \widehat{ACC''} \cong \widehat{AC''C} $$
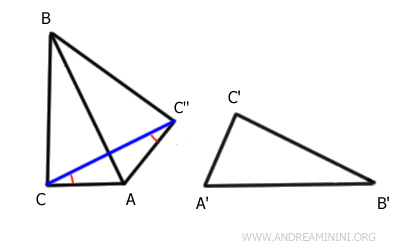
El triángulo CBC'' es también isósceles, con base $ \overline{CC''} $, pues $ \overline{BC} \cong \overline{BC''} $.
Por tanto:
$$ \widehat{BCC''} \cong \widehat{BC''C} $$
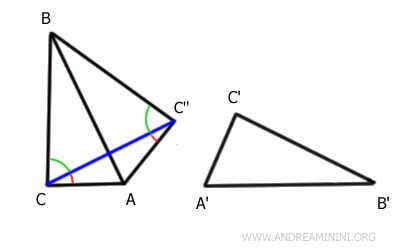
La suma de estos ángulos también es congruente:
$$ \widehat{ACB} \cong \widehat{AC''B} $$
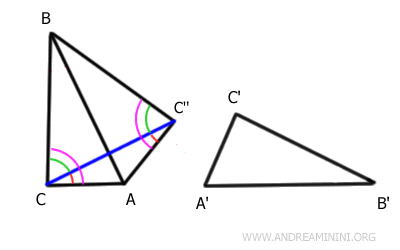
Además, como $ \overline{AC} \cong \overline{AC''} $ y $ \overline{BC} \cong \overline{BC''} $, por el primer criterio de congruencia:
$$ ABC \cong ABC'' $$
Como $ ABC'' \cong A'B'C' $, por transitividad:
$$ ABC \cong A'B'C' $$
Que es lo que queríamos demostrar.
Demostración alternativa
Consideremos dos triángulos ABC y A'B'C' con lados correspondientes congruentes:
$$ \overline{AB} \cong \overline{A'B'} $$
$$ \overline{BC} \cong \overline{B'C'} $$
$$ \overline{AC} \cong \overline{A'C'} $$
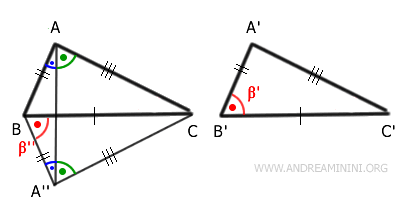
Construimos un rayo $ A''B $ que forme el mismo ángulo $ \beta' $ en el vértice B, con $ \overline{A''B} \cong \overline{A'B'} $.
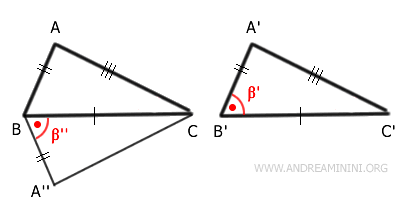
Los triángulos $ A''BC $ y $ A'B'C' $ tienen:
- Un lado congruente: $ \overline{BC} \cong \overline{B'C'} $
- Otro lado congruente: $ \overline{A''B} \cong \overline{A'B'} $
- Ángulo comprendido congruente: $ \beta' \cong \beta'' $
Por el primer criterio de congruencia:
$$ A''BC \cong A'B'C' $$
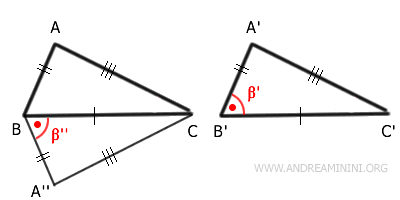
Luego unimos A y A'' con $ \overline{AA''} $. El triángulo $ ABA'' $ es isósceles:
$$ \overline{AB} \cong \overline{A''B} $$
y por tanto:
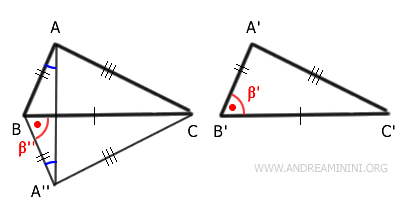
Del mismo modo, $ ACA'' $ es isósceles:
Finalmente, por el primer criterio de congruencia:
$$ ABC \cong A''BC $$
Como $ A''BC \cong A'B'C' $, se concluye:
$$ ABC \cong A'B'C' $$
Demostración completa.
Y así sucesivamente.