Altura de un Triángulo
La altura (h) de un triángulo es un segmento perpendicular que une un vértice con el lado opuesto o con su prolongación.
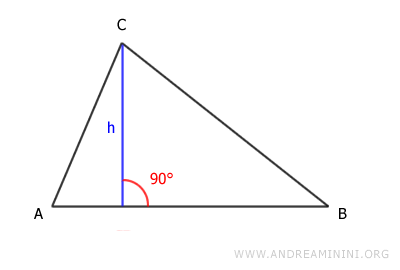
En otras palabras, es la distancia perpendicular desde un vértice hasta la base elegida.
La altura forma dos ángulos rectos con la base.
Dado que un triángulo tiene tres lados y cualquiera de ellos puede considerarse base, todo triángulo posee tres alturas.
Por ejemplo, si se toma el lado CB como base, la altura se traza así:
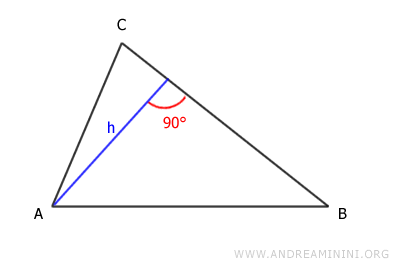
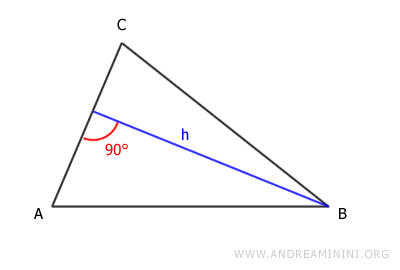
Si se elige el lado AC como base, la altura es la siguiente:
La altura (h) también puede situarse fuera del triángulo, ya que en ocasiones es perpendicular a la prolongación de la base.
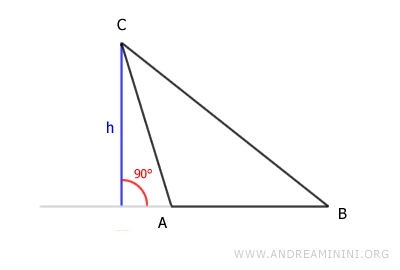
Este hecho distingue a la altura de la bisectriz y de la mediana, que siempre son segmentos internos al triángulo.
Cómo Calcular la Altura de un Triángulo
La fórmula para calcular la altura de un triángulo es:
$$ h = \frac{2A}{b} $$
Donde A es el área del triángulo y b la longitud de la base.
Para hallar la altura, basta con dividir el doble del área entre la longitud de la base.
Nota: Esta fórmula se deduce del hecho de que el área (A) de un triángulo es igual al producto de la base por la altura, dividido entre dos. $$ A = \frac{b \cdot h}{2} $$ Despejando h, multiplicamos ambos miembros por dos: $$ 2 \cdot A = b \cdot h $$ Después, dividimos entre la base y simplificamos: $$ h = \frac{2A}{b} $$
Un Ejemplo Práctico
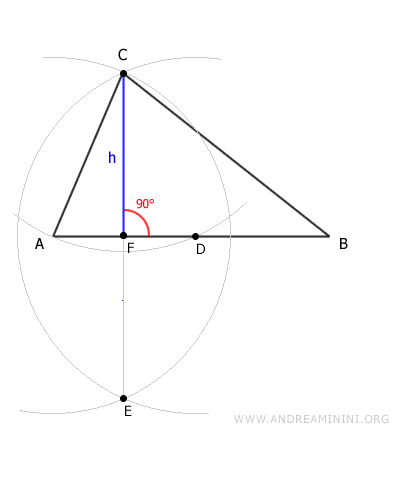
Consideremos el triángulo ABC.
Tomamos el segmento AB como base.
Se traza un segmento perpendicular a la base AB que pase por el vértice opuesto C.
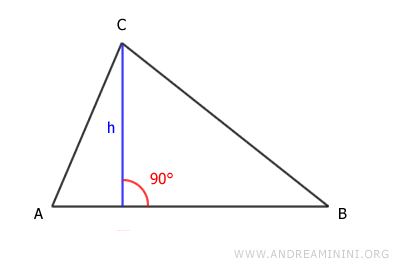
Este segmento es la altura del triángulo.
Cómo determinar la altura de un triángulo: Para calcular la altura relativa a la base AB, coloca la punta del compás en el vértice C y traza un arco de radio AC para ubicar el punto D.
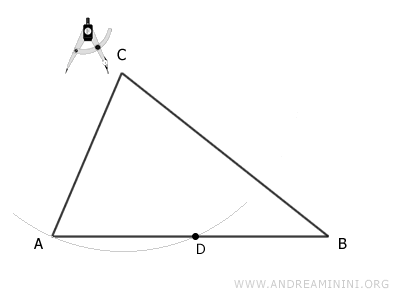
Sin variar la apertura del compás, dibuja un arco con centro en A y otro con centro en D. El punto donde se intersectan estos dos arcos determina el punto E, ubicado fuera del triángulo.
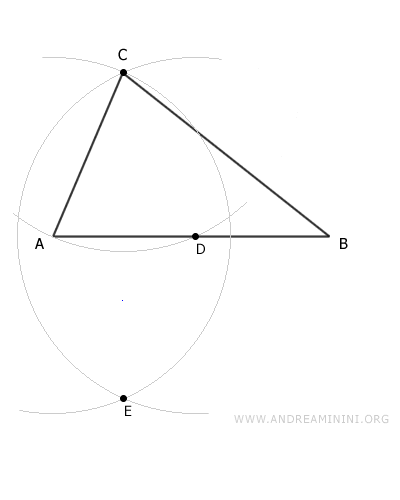
Une el punto E con el vértice C mediante el segmento EC, que corta la base en el punto F. El segmento EC es perpendicular a la base y forma un ángulo recto. La altura del triángulo es el segmento CF.
Altura de un Triángulo Equilátero
La altura de un triángulo equilátero se calcula con la siguiente fórmula: \[ h = \frac{\sqrt{3}}{2} \cdot l \] donde \( h \) es la altura y \( l \) la longitud de uno de sus lados.
Esta fórmula se obtiene a partir de las propiedades geométricas de un triángulo equilátero.
Conocer la longitud de uno de sus lados es suficiente para determinar su altura.
Ejemplo
Consideremos un triángulo equilátero ABC cuyos lados miden 6 unidades.
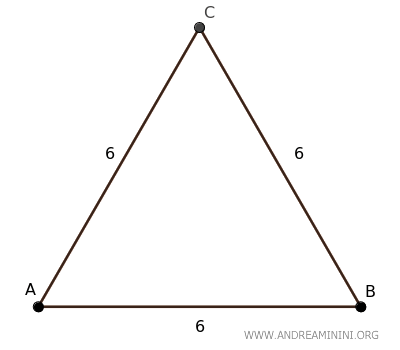
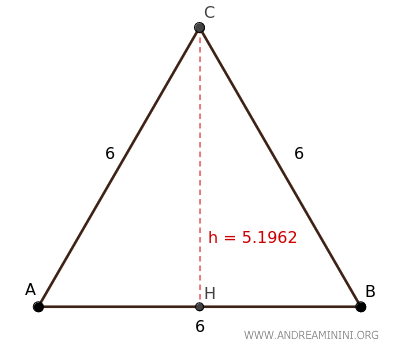
Para calcular su altura, empleamos la fórmula:
$$ h = \frac{\sqrt{3}}{2} \cdot l $$
Siendo \( l = 6 \):
$$ h = \frac{\sqrt{3}}{2} \cdot 6 $$
$$ h = 3 \cdot \sqrt{3} $$
$$ h \approx 5.1962 $$
Por tanto, la altura del triángulo equilátero es aproximadamente 5.1962 unidades.
Demostración
Un triángulo equilátero posee sus tres lados de igual longitud.
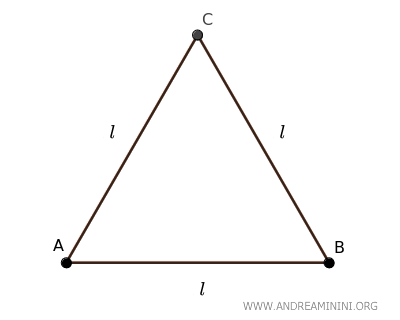
Si se traza una altura desde uno de sus vértices hacia el lado opuesto, el triángulo equilátero queda dividido en dos triángulos rectángulos congruentes, \( \triangle ACH \cong \triangle BCH \).
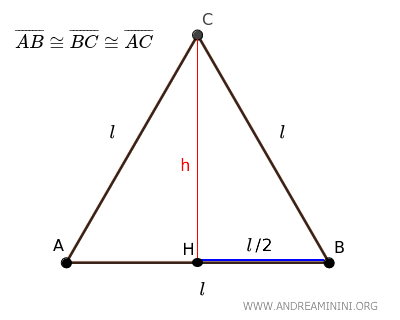
En cada uno de estos triángulos rectángulos, la altura \( h \) es uno de los catetos, la mitad de la base \( \frac{l}{2} \) es el otro cateto, y el lado del triángulo equilátero \( l \) actúa como hipotenusa.
Para hallar la longitud de la altura, aplicamos el teorema de Pitágoras:
$$ l^2 = h^2 + \left(\frac{l}{2}\right)^2 $$
$$ l^2 = h^2 + \frac{l^2}{4} $$
Despejando \( h \):
$$ h^2 = l^2 - \frac{l^2}{4} $$
$$ h^2 = \frac{3l^2}{4} $$
Extrayendo la raíz cuadrada en ambos miembros:
$$ h = \sqrt{\frac{3l^2}{4}} $$
$$ h = \frac{\sqrt{3}}{2} \cdot l $$
Por tanto, la altura \( h \) de un triángulo equilátero de lado \( l \) se expresa como \(\frac{\sqrt{3}}{2} \times l\).
Ortocentro
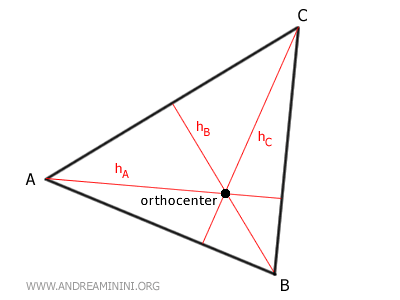
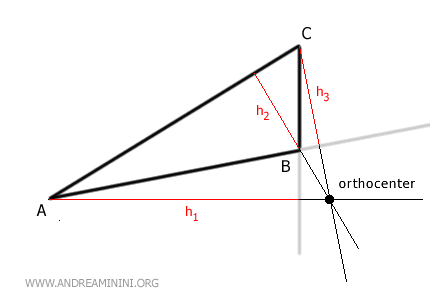
El ortocentro es el punto de intersección de las tres alturas de un triángulo.
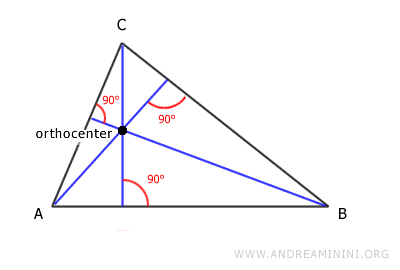
Su posición varía según los ángulos del triángulo:
- Dentro del triángulo
Si el triángulo es acutángulo, es decir, todos sus ángulos son menores de 90 grados, el ortocentro se ubica en el interior.
- Fuera del triángulo
Si el triángulo es obtusángulo, es decir, posee un ángulo mayor de 90 grados, el ortocentro se encuentra fuera del triángulo.
- En uno de los vértices
Si el triángulo es rectángulo, es decir, tiene un ángulo de 90 grados, el ortocentro coincide con el vértice del ángulo recto.
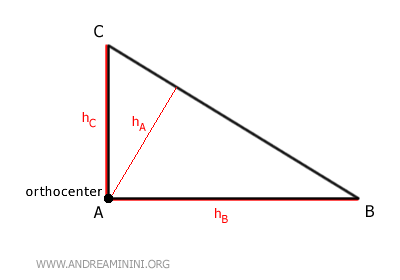
Y así sucesivamente.