Recta de Euler
La Recta de Euler es la línea que pasa por el ortocentro, el baricentro y el circuncentro de un triángulo.
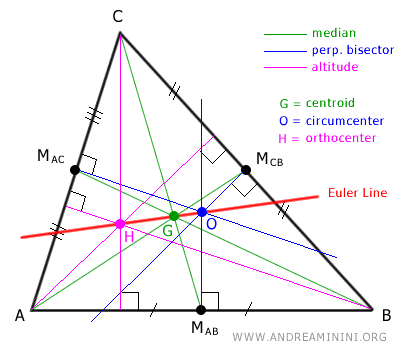
Esta construcción geométrica conecta varios puntos notables del triángulo.
En cualquier triángulo existen tres puntos fundamentales: el baricentro (G), el circuncentro (O) y el ortocentro (H).
Independientemente de la forma o el tamaño del triángulo, salvo en el caso de los triángulos equiláteros, estos tres puntos siempre están alineados.
La Recta de Euler recibe su nombre en honor al matemático suizo Leonhard Euler, considerado uno de los más grandes matemáticos de todos los tiempos y célebre por sus aportes en múltiples campos de las matemáticas.
Un ejemplo práctico
Consideremos un triángulo cualquiera ABC.
Primero, identificamos el baricentro.
El baricentro (G) es el punto donde se intersectan las medianas del triángulo.
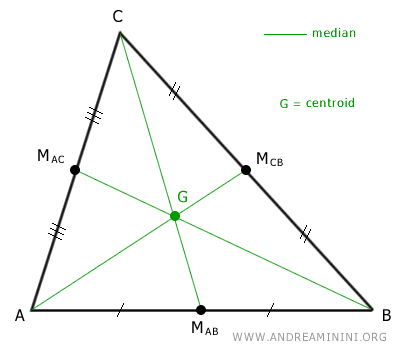
Una mediana es un segmento que une un vértice (A, B o C) del triángulo con el punto medio (MAB, MBC, MAC) del lado opuesto.
Nota: El baricentro divide cada mediana en una proporción 2:1, siendo el segmento más largo el que va del vértice (A, B o C) al baricentro (G).
A continuación, localizamos el circuncentro.
El circuncentro (O) es el punto donde se cortan las mediatrices perpendiculares de los lados del triángulo, las cuales pasan por los puntos medios de dichos lados.
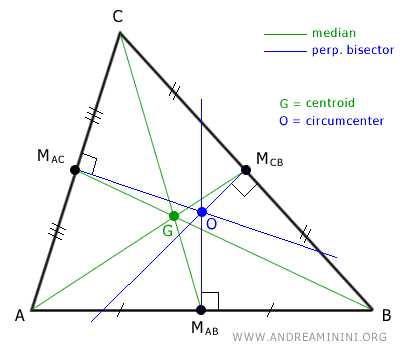
Nota: El circuncentro (O) es además el centro de la circunferencia circunscrita, es decir, la circunferencia que pasa por los tres vértices del triángulo.
Por último, determinamos el ortocentro.
El ortocentro (H) es el punto de intersección de las alturas del triángulo.
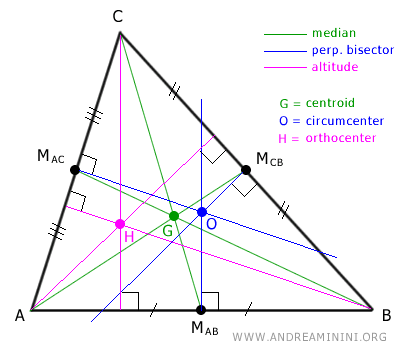
Una altura es un segmento perpendicular trazado desde un vértice hasta el lado opuesto o su prolongación.
Estos tres puntos, G, O y H, se encuentran alineados.
La línea que pasa por estos tres puntos se denomina Recta de Euler.

Observaciones
A continuación, algunas observaciones sobre la Recta de Euler:
- En la Recta de Euler, el baricentro (G) se sitúa entre el circuncentro (O) y el ortocentro (H).

- La distancia entre el baricentro y el ortocentro (GH) es el doble de la distancia entre el baricentro y el circuncentro (GO). $$ GH = 2GO $$ En consecuencia, la distancia entre el circuncentro y el ortocentro (OH) es tres veces la distancia entre el baricentro y el circuncentro (GO). $$ OH = 3GO $$
- El caso del triángulo equilátero
La Recta de Euler no existe en los triángulos equiláteros, ya que el ortocentro, el baricentro y el circuncentro coinciden en un mismo punto (H = I = G = O). Por tanto, en los triángulos equiláteros estos puntos no están alineados, y en lugar de una sola recta, existe un haz infinito de rectas que pasan por el mismo punto.
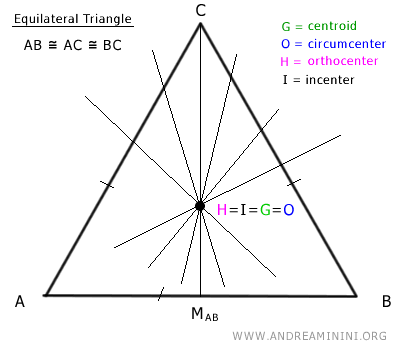
- Otros puntos notables del triángulo
La Recta de Euler también pasa por otros puntos notables del triángulo, como el punto de Longchamps, el punto de Schiffler, el punto de Exeter y el punto de Gossard. - El incentro
En general, el incentro no se encuentra sobre la Recta de Euler, salvo en el caso de triángulos isósceles, donde sí está alineado con el ortocentro, el baricentro y el circuncentro.
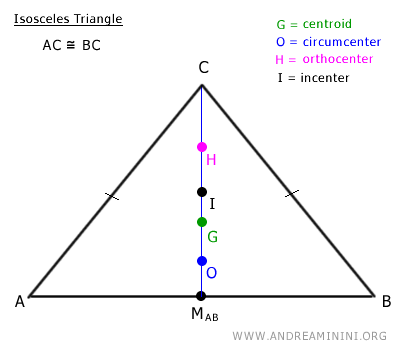
- El caso de los triángulos isósceles
En los triángulos isósceles, la Recta de Euler coincide con el eje de simetría del triángulo.
Y así sucesivamente.