Radio de la Circunferencia Circunscrita a un Triángulo

El radio de la circunferencia que circunscribe a un triángulo se obtiene dividiendo el producto de las longitudes de sus lados (a · b · c) entre cuatro veces su área (A), según la fórmula: $$ r = \frac{a \cdot b \cdot c}{4 \cdot A} $$ Aquí, a, b y c representan las longitudes de los lados del triángulo, y A es su área.

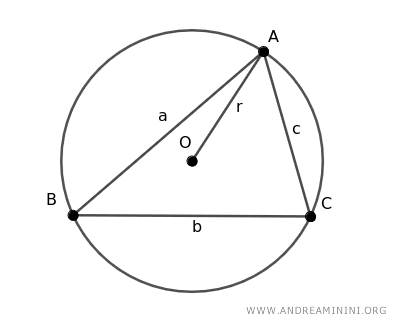
Esta fórmula está estrechamente vinculada a la fórmula de Herón, que permite calcular el área de un triángulo a partir de su semiperímetro.

$$ A = \sqrt{p \cdot (p - a) \cdot (p - b) \cdot (p - c)} $$

Donde p es el semiperímetro del triángulo, calculado como p = (a + b + c)/2.

Al sustituir la fórmula de Herón en la expresión para r, se obtiene una relación directa entre los lados del triángulo (a, b, c), su semiperímetro (p) y el radio (r) de la circunferencia circunscrita:

$$ r = \frac{a \cdot b \cdot c}{4 \cdot A} = \frac{a \cdot b \cdot c}{4 \cdot \sqrt{p \cdot (p - a) \cdot (p - b) \cdot (p - c)}} $$

De este modo, no es necesario calcular el área (A); basta con conocer las longitudes de los lados $a$, $b$ y $c$ del triángulo. En muchas ocasiones, este recurso resulta sumamente práctico.

Gracias a las relaciones geométricas entre la circunferencia circunscrita y las propiedades del triángulo, es posible vincular el radio r de la circunferencia con el área A y los lados del triángulo. Para más detalles, consulta la demostración que se presenta a continuación.

Ejemplo Práctico

Para ilustrar el uso de la fórmula, consideremos una circunferencia con centro O y radio OA = 3, en la que está inscrito el triángulo ABC.

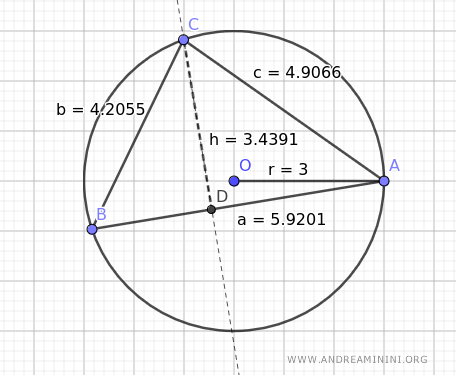
Queremos comprobar la validez de la fórmula:

$$ r = \frac{a \cdot b \cdot c}{4 \cdot A} $$

Usamos las siguientes longitudes para los lados: a = 5.9201, b = 4.9066 y c = 4.2055:

$$ r = \frac{5.9201 \cdot 4.9066 \cdot 4.2055}{4 \cdot A} $$

$$ r = \frac{122.1586}{4 \cdot A} $$

El área del triángulo, calculada como la mitad del producto de su base y su altura, es:

$$ A = \frac{a \cdot h}{2} = \frac{5.9201 \cdot 3.4391}{2} = 10.1799 $$

Al sustituir A = 10.1799 en la fórmula del radio:

$$ r = \frac{122.1586}{4 \cdot 10.1799} \approx 3 $$

Este resultado confirma que el radio de la circunferencia circunscrita es r = 3 alrededor del triángulo.

Así, se verifica la coherencia del valor inicial proporcionado en el ejemplo, demostrando la utilidad y precisión de la fórmula.

Demostración

Imaginemos una circunferencia con centro O y radio OA.

Seleccionamos tres puntos distintos A, B y C sobre la circunferencia y trazamos los segmentos que conforman el triángulo ABC.

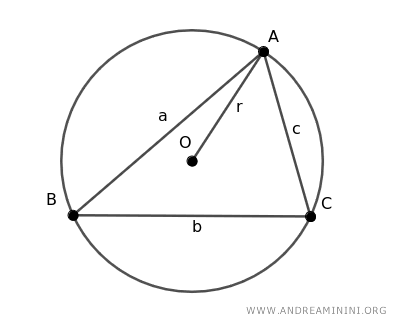
Después, dibujamos el diámetro de la circunferencia (d) y la altura (h) del triángulo.

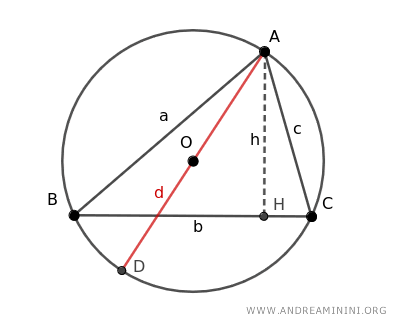
Esta construcción genera dos triángulos rectángulos: AHC y ABD.

1. El triángulo AHC es rectángulo, ya que la altura h es perpendicular a la base BC y funciona como altura del triángulo ABC.
2. El triángulo ABD también es rectángulo porque el segmento AD es el diámetro de la circunferencia, y se sabe que cualquier triángulo inscrito en un semicírculo es rectángulo.

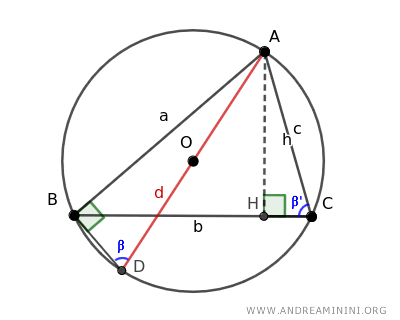
La congruencia de ciertos ángulos en los triángulos AHC y ABD refuerza su semejanza:

1. El ángulo recto de 90°.
2. Los ángulos agudos β y β′, que son congruentes porque abarcan el mismo arco AB y, por lo tanto, miden lo mismo.

Por lo tanto, según los criterios de semejanza de triángulos, los triángulos AHC y ABD tienen ángulos congruentes y lados proporcionales, lo cual demuestra que son semejantes:

$$ AHC \approx ABD $$

De esta semejanza se deduce la siguiente relación entre sus lados correspondientes:

$$ a : h = d : c $$

Dado que el diámetro d equivale al doble del radio (2r), podemos reescribir la relación así:

$$ a : h = 2r : c $$

Expresándolo como fracción:

$$ \frac{a}{h} = \frac{2r}{c} $$

Y despejando el radio:

$$ r = \frac{a \cdot c}{2h} $$

Para simplificar aún más, multiplicamos y dividimos el segundo miembro por b:

$$ r = \frac{a \cdot c}{2h} \cdot \frac{b}{b} $$

$$ r = \frac{a \cdot b \cdot c}{2h \cdot b} $$

Como el producto h · b equivale al doble del área del triángulo (ya que A = (h · b)/2), entonces h · b = 2A, lo que permite escribir:

$$ r = \frac{a \cdot b \cdot c}{2 \cdot (2A)} $$

$$ r = \frac{a \cdot b \cdot c}{4A} $$

Así se demuestra, de manera rigurosa, que el radio de la circunferencia circunscrita a un triángulo es igual al producto de sus lados dividido entre cuatro veces su área.

Esta demostración no solo confirma la validez de la fórmula, sino que también enriquece nuestra comprensión de la relación geométrica entre un triángulo y su circunferencia circunscrita.