Radio de la Circunferencia Inscrita en un Triángulo
El radio de una circunferencia inscrita en un triángulo se calcula dividiendo el área del triángulo (A) entre su semiperímetro (p): $$ r = \frac{A}{p} $$
Esta fórmula revela un vínculo fascinante entre el área del triángulo, su perímetro y el radio de la circunferencia inscrita.
Es una herramienta muy útil para resolver problemas relacionados con las propiedades de triángulos y circunferencias.
Ejemplo Práctico
Tomemos como ejemplo el triángulo ABC.
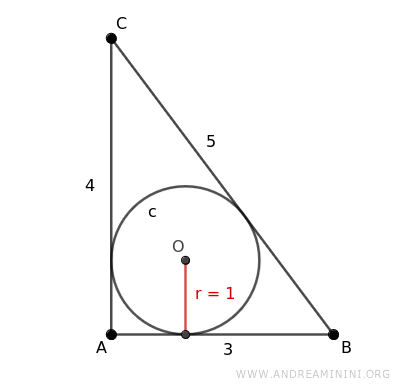
Sus lados miden AB=3, AC=4 y BC=5, y el radio de la circunferencia inscrita es r=1.
Por tanto, el semiperímetro del triángulo ABC es p=6:
$$ 2p = 3+4+5 $$
$$ 2p = 12 $$
$$ p = 6 $$
Calculamos el área del triángulo, que resulta ser A=6, usando la fórmula de base por altura dividido entre dos, con base AB=3 y altura AC=4:
$$ Area_{ABC} = \frac{ \overline{AB} \cdot \overline{AC} }{2} $$
$$ Area_{ABC} = \frac{ 3 \cdot 4 }{2} = \frac{12}{2} = 6 $$
Ahora hallamos la razón entre el área A=6 y el semiperímetro p=6 del triángulo:
$$ r = \frac{Area_{ABC}}{p} = \frac{6}{6} = 1 $$
Este cálculo nos da el valor del radio de la circunferencia inscrita.
Nota: Para simplificar, en este ejemplo se ha utilizado un triángulo rectángulo, pero la fórmula es válida para cualquier tipo de triángulo.
Demostración
Consideremos un triángulo cualquiera, llamado ABC.
Para encontrar el incentro, es decir, el centro de la circunferencia inscrita, trazamos las bisectrices de los ángulos del triángulo ABC.
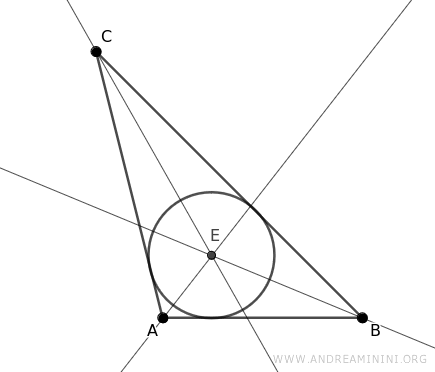
La circunferencia inscrita es tangente a los tres lados del triángulo en los puntos D, F y G. Los segmentos EF, EG y EH representan los radios de la circunferencia y, por definición, son iguales: EF ≅ EG ≅ EH.
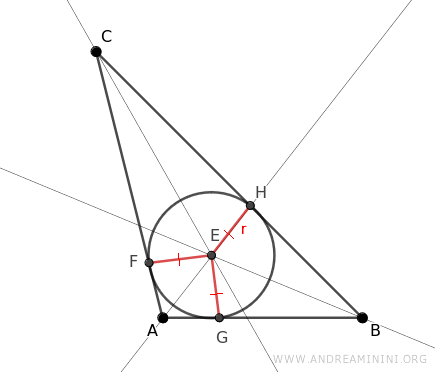
Además, estos radios son perpendiculares a los lados del triángulo en los puntos de tangencia, convirtiéndose en las alturas de los triángulos menores ACE, ABE y BCE formados dentro del triángulo ABC.
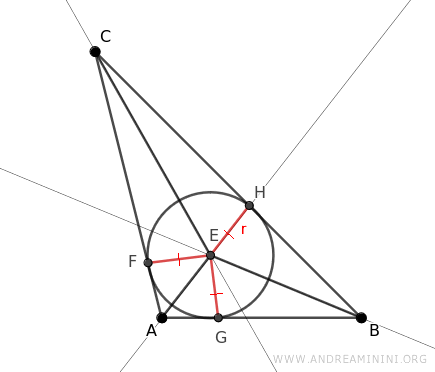
La suma de las áreas de los triángulos ACE, ABE y BCE es exactamente igual al área del triángulo mayor ABC, lo cual refleja una bella simetría geométrica:
$$ \text{Area}_{ABC} = \text{Area}_{ACE} + \text{Area}_{ABE} + \text{Area}_{BCE} $$
Para calcular el área de un triángulo, multiplicamos la base por la altura y dividimos entre dos. En este caso, la base de cada triángulo menor es un lado de ABC, y la altura es el radio (r) de la circunferencia inscrita.
$$ \text{Area}_{ABC} = \frac{ \overline{AC} \cdot r }{2} + \frac{ \overline{AB} \cdot r }{2} + \frac{ \overline{BC} \cdot r }{2} $$
Factorizando el radio r:
$$ \text{Area}_{ABC} = r \cdot \left( \frac{ \overline{AC} }{2} + \frac{ \overline{AB} }{2} + \frac{ \overline{BC} }{2} \right) $$
$$ \text{Area}_{ABC} = r \cdot \left( \frac{ \overline{AC} + \overline{AB} + \overline{BC} }{2} \right) $$
La suma de los lados AC + AB + BC = P corresponde al perímetro (P) del triángulo ABC, que es el doble de su semiperímetro P = 2p.
$$ \text{Area}_{ABC} = r \cdot \left( \frac{ 2p }{2} \right) $$
$$ \require{cancel} \text{Area}_{ABC} = r \cdot \left( \frac{ \cancel{2} \, p }{ \cancel{2} } \right) $$
$$ \text{Area}_{ABC} = r \cdot p $$
Así, queda demostrada de forma elegante que el área del triángulo ABC es igual al producto del radio de la circunferencia inscrita (r) por el semiperímetro (p) del triángulo.
Y esto es solo el principio.