Ecuación de la Recta
La forma explícita de la ecuación de la recta es $$ y = mx + q $$ donde m representa la pendiente y q es la ordenada al origen, es decir, el punto donde la recta corta al eje y.
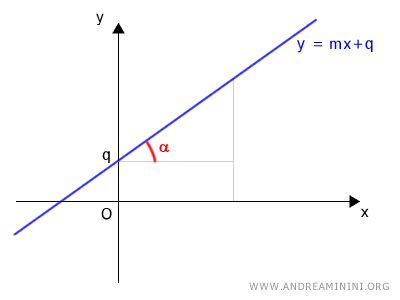
Se denomina forma explícita porque y está expresada como función de x.
$$ y = mx + q $$
En esta ecuación, y es la variable dependiente y x es la variable independiente.
Al variar la pendiente m, se modifica la inclinación de la recta.
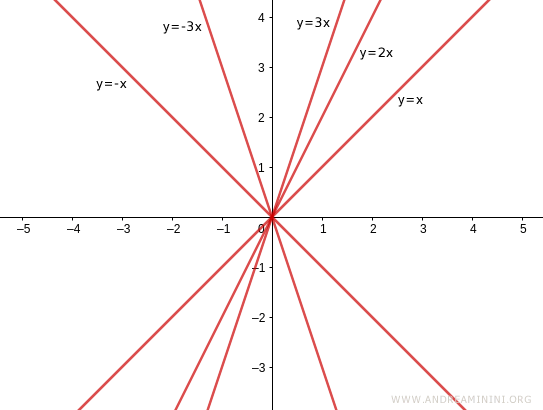
Por su parte, al modificar la ordenada al origen q, se desplaza el punto donde la recta intersecta el eje y.
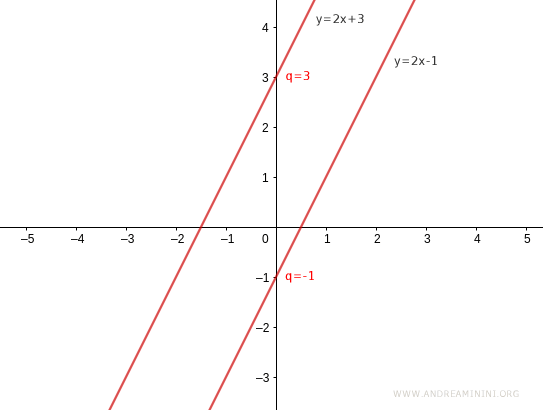
Por lo tanto, la forma explícita permite representar cualquier recta en el plano, salvo aquellas paralelas o coincidentes con el eje y.
El caso de las rectas paralelas o coincidentes con el eje y
Para describir el eje y se utiliza una ecuación diferente:
$$ x = 0 $$
Para las rectas paralelas al eje y, se emplea la ecuación:
$$ x = k $$
Nota. El eje y no puede representarse mediante la ecuación explícita y = mx + q, ya que la pendiente m es indefinida para una recta vertical.
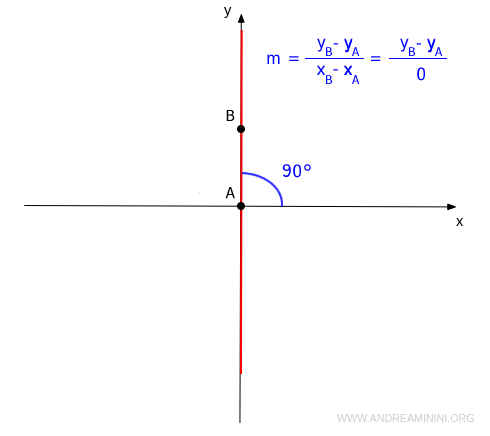
No existen valores de m ni de q que puedan sustituirse en la ecuación y = mx + q para representar una recta vertical. Por eso, cualquier recta paralela al eje y se describe mediante $$ x = k $$ Al variar k, se obtienen todas las rectas paralelas al eje y, independientemente de y. Para k = 0, se obtiene el propio eje y.
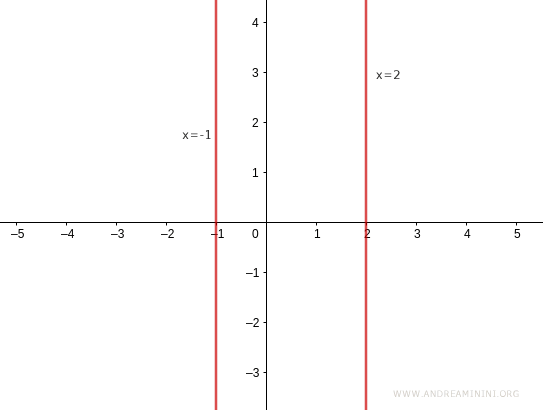
La Forma Implícita de la Ecuación
La forma implícita de la ecuación de la recta es otra forma de expresar rectas en el plano: $$ ax + by + c = 0 $$ donde a, b y c son números reales denominados coeficientes. También se la conoce como la forma general de la ecuación de la recta.
En la forma implícita, ni x ni y se expresan de manera explícita como función de la otra variable.
Al variar los coeficientes a, b y c, la ecuación implícita permite representar cualquier recta en el plano cartesiano.
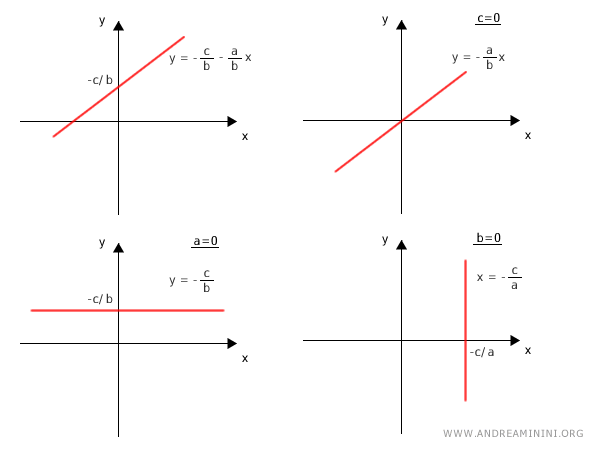
Nota. En la ecuación ax + by + c = 0, los coeficientes a y b no pueden ser simultáneamente cero.
La forma implícita tiene la ventaja de poder representar también rectas paralelas o coincidentes con el eje y.
Por ello, también se la conoce como la forma general de la ecuación de la recta.
Nota. Para describir una recta vertical, basta con hacer b = 0 y resolver respecto a x:
$$ ax + by + c = 0 $$
$$ ax + 0 \cdot y + c = 0 $$
$$ ax + c = 0 $$
$$ x = - \frac{c}{a} $$
Demostración
Consideremos dos puntos P1(x1, y1) y P2(x2, y2) en el plano cartesiano, por los cuales pasa una recta r, y un punto P(x, y) ubicado sobre dicha recta, entre P1 y P2.
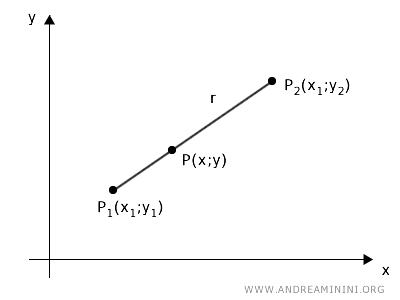
Proyectamos los puntos sobre los ejes coordenados mediante dos familias de rectas paralelas.
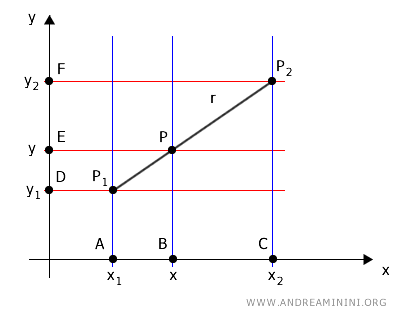
El conjunto de rectas verticales, de color azul y paralelas al eje y, corta a dos transversales: la recta r y el eje x.
De acuerdo con el teorema de Tales, los segmentos correspondientes sobre las transversales son proporcionales.
$$ \frac{ \overline{P_1P} }{ \overline{AB} } = \frac{ \overline{P_1P_2} }{ \overline{AC} } $$
$$ \frac{ \overline{P_1P} }{ \overline{P_1P_2} } = \frac{ \overline{AB} }{ \overline{AC} } $$
De manera análoga, el conjunto de rectas horizontales, de color rojo y paralelas al eje x, corta a dos transversales: la recta r y el eje y.
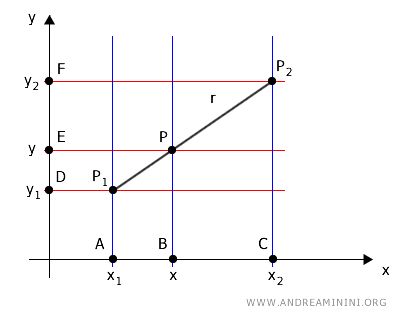
Nuevamente, según el teorema de Tales, los segmentos correspondientes sobre las transversales son proporcionales.
$$ \frac{ \overline{P_1P} }{ \overline{DE} } = \frac{ \overline{P_1P_2} }{ \overline{DF} } $$
$$ \frac{ \overline{P_1P} }{ \overline{P_1P_2} } = \frac{ \overline{DE} }{ \overline{DF} } $$
De estas dos proporciones se deduce la igualdad entre las razones AB/AC y DE/DF:
$$ \frac{ \overline{P_1P} }{ \overline{P_1P_2} } = \frac{ \overline{AB} }{ \overline{AC} } = \frac{ \overline{DE} }{ \overline{DF} } $$
Es decir:
$$ \frac{ \overline{AB} }{ \overline{AC} } = \frac{ \overline{DE} }{ \overline{DF} } $$
Sabiendo que AB = x - x1 y AC = x2 - x1, se obtiene:
$$ \frac{ x - x_1 }{ x_2 - x_1 } = \frac{ \overline{DE} }{ \overline{DF} } $$
Y dado que DE = y - y1 y DF = y2 - y1:
$$ \frac{ x - x_1 }{ x_2 - x_1 } = \frac{ y - y_1 }{ y_2 - y_1 } $$
Esta última relación se conoce como la condición de colinealidad de tres puntos sobre una misma recta.
Mediante transformaciones algebraicas, podemos reordenar la ecuación anterior:
$$ ( x - x_1 ) \cdot ( y_2 - y_1 ) = ( y - y_1 ) \cdot ( x_2 - x_1 ) $$
$$ x \cdot ( y_2 - y_1 ) - x_1 \cdot ( y_2 - y_1 ) = y \cdot ( x_2 - x_1 ) - y_1 \cdot ( x_2 - x_1 ) $$
$$ x \cdot ( y_2 - y_1 ) - x_1 \cdot ( y_2 - y_1 ) - y \cdot ( x_2 - x_1 ) + y_1 \cdot ( x_2 - x_1 ) = 0 $$
$$ \require{cancel} x \cdot ( y_2 - y_1 ) - y \cdot ( x_2 - x_1 ) - x_1 y_2 + \cancel{ x_1 y_1 } + x_2 y_1 - \cancel{ x_1 y_1 } = 0 $$
$$ x \cdot ( y_2 - y_1 ) - y \cdot ( x_2 - x_1 ) - x_1 y_2 + x_2 y_1 = 0 $$
Reescribimos -y( x2 - x1 ) como +y( x1 - x2 ):
$$ x \cdot ( y_2 - y_1 ) + y \cdot ( x_1 - x_2 ) - x_1 y_2 + x_2 y_1 = 0 $$
Finalmente, definimos a = ( y2 - y1 ), b = ( x1 - x2 ), c = - x1 y2 + x2 y1:
$$ x \cdot a + y \cdot b + c = 0 $$
Así, obtenemos la forma implícita de la ecuación de la recta:
$$ ax + by + c = 0 $$
Cómo Convertir de la Forma Implícita a la Explícita
Para transformar la ecuación en forma implícita $ ax + by + c = 0 $ a la forma explícita $ y = mx + q $, basta con despejar y.
$$ y = - \frac{ax}{b} - \frac{c}{b} $$
$$ y = - \frac{a}{b} \cdot x - \frac{c}{b} $$
Aquí, $ -\frac{a}{b} $ es la pendiente y $ -\frac{c}{b} $ corresponde a la ordenada al origen.
$$ m = - \frac{a}{b} $$
$$ q = - \frac{c}{b} $$
Este procedimiento solo es posible siempre que el coeficiente b sea distinto de cero.
Nota. La conversión de forma implícita a explícita no es viable si b = 0, pues implicaría una división por cero.
Ejemplo
Consideremos la ecuación de una recta en forma implícita con a = 3, b = 6 y c = 9:
$$ 3y + 6x + 9 = 0 $$
Para expresarla en forma explícita, despejamos y:
$$ 3y = -6x - 9 $$
Dividimos ambos miembros de la ecuación por 3, aplicando la propiedad invariantiva:
$$ \frac{3y}{3} = - \frac{6}{3}x - \frac{9}{3} $$
$$ y = -2x - 3 $$
Esta es la ecuación de la recta en forma explícita:
$$ y = mx + q $$
Donde la pendiente es m = -2 y la ordenada al origen es q = -3.
¿Cuál es la diferencia entre la forma implícita y la explícita? Ambas representan exactamente la misma recta en el plano. La diferencia radica en la forma en que se expresa la relación entre las variables.
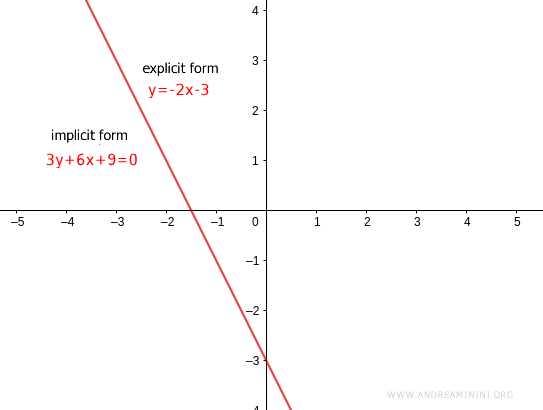
La Forma Implícita de una Recta como Intersección de Dos Planos
Cualquier recta en el espacio tridimensional puede describirse como la intersección de dos planos no paralelos, representados mediante un sistema de dos ecuaciones lineales:
$$ \begin{cases} a_1 x + b_1 y + c_1 z + d_1 = 0 \\ \\ a_2 x + b_2 y + c_2 z + d_2 = 0 \end{cases} $$
En geometría analítica, una recta en el espacio (en $\mathbb{R}^3$) puede representarse de diversas formas.
Una de las más utilizadas es la llamada forma implícita, que expresa la recta como un sistema de dos ecuaciones de plano.
Cada plano en el espacio está definido por una ecuación de la forma:
$$ a x + b y + c z + d = 0 $$
Si tomamos dos planos distintos que se intersecan, el sistema de ecuaciones se escribe así:
$$
\begin{cases}
a_1 x + b_1 y + c_1 z + d_1 = 0 \\ \\
a_2 x + b_2 y + c_2 z + d_2 = 0
\end{cases}
$$
Estas son las ecuaciones generales de la recta, donde cada ecuación representa uno de los planos.
Este sistema define la recta de manera implícita, imponiendo dos restricciones simultáneas sobre los puntos $(x, y, z)$. Los puntos que satisfacen ambas ecuaciones pertenecen a ambos planos y, por tanto, se encuentran en su intersección.
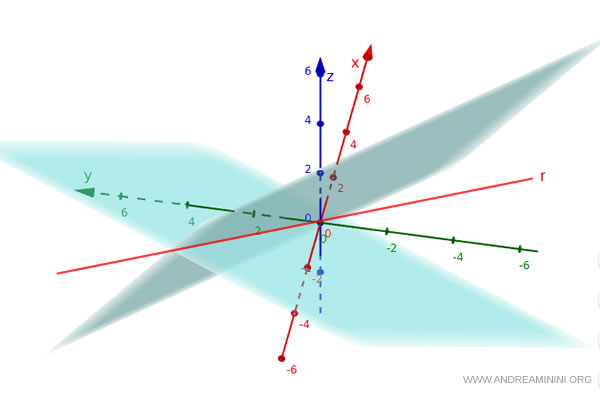
La intersección de dos planos distintos (no paralelos) es precisamente una recta $ r $.

Por supuesto, el sistema que representa la recta no es único, ya que existen infinitos pares de planos diferentes que pueden intersectarse exactamente en la misma recta $ r $.

El conjunto de todos los planos que contienen la misma recta $ r $ se denomina haz de planos.
¿Por qué se denomina forma implícita? Se llama implícita porque no expresa de manera explícita las coordenadas de la recta en función de un parámetro, ni revela de inmediato si la recta pasa por un punto específico o cuál es su dirección. En su lugar, define la recta mediante dos restricciones (las dos ecuaciones de plano), y la recta surge precisamente como su intersección.
Ejemplo
Consideremos los siguientes dos planos:
$$
\begin{cases}
x + y + z - 1 = 0 \\
2x - y + 3z + 4 = 0
\end{cases}
$$
El conjunto de puntos $(x, y, z)$ que satisface simultáneamente ambas ecuaciones constituye una recta en el espacio.
Ecuaciones de la Recta en Forma Bivariante
Este método describe una recta en el espacio tridimensional expresando dos de sus coordenadas en función de la tercera.
Por ejemplo, se pueden expresar \( x \) e \( y \) en función de \( z \):
$$ \begin{cases} a_1 x + b_1 y + c_1 z + d_1 = 0 \\ \\ a_2 x + b_2 y + c_2 z + d_2 = 0 \end{cases}\quad\Longrightarrow\quad \begin{cases} x = gz + p \\ \\ y = hz + q \end{cases} $$
O bien expresar \( x \) y \( z \) en función de \( y \):
$$ \begin{cases} x = ky + r \\ \\ z = jy + s \end{cases} $$
O expresar \( y \) y \( z \) en función de \( x \):
$$ \begin{cases} y = mx + t \\ \\ z = nx + u \end{cases} $$
Esta representación constituye una parametrización implícita de la recta, ya que no introduce un parámetro auxiliar como \( t \).
Al asignar valores arbitrarios a la variable independiente (por ejemplo, \( z \)), se obtienen puntos concretos que pertenecen a la recta.
Nota. La elección de qué variable utilizar como parámetro depende de la orientación de la recta en el espacio. Por ejemplo, si la recta es paralela al plano \( xy \), la coordenada \( z \) permanece constante a lo largo de la recta. En tal caso, \( z \) no puede elegirse como parámetro, ya que no varía: $$ \begin{cases} x = gz + p \\ \\ y = hz + q \end{cases} $$ Lo mismo sucede si la recta es paralela al plano \( xz \) o \( yz \): entonces no se puede elegir \( y \) o \( x \), respectivamente, ya que esas coordenadas permanecen fijas. Por ello, al expresar una recta de este modo, siempre se debe escoger una variable que efectivamente varíe a lo largo de la recta.
Ejemplo
Consideremos la recta definida por el sistema:
$$ \begin{cases} x + y - z = 0 \quad \text{(1)} \\ 2x - y + 3z = 5 \quad \text{(2)} \end{cases} $$
Vamos a hallar la forma bivariante resolviendo el sistema para \( x \) e \( y \) en términos de \( z \).
Comenzamos sumando las dos ecuaciones para eliminar \( y \):
$$ \begin{cases} x + 2x + y - y - z + 3z = 0 + 5 \\ 2x - y + 3z = 5 \end{cases} $$
$$ \begin{cases} 3x + 2z = 5 \\ 2x - y + 3z = 5 \end{cases} $$
Despejamos \( x \) en la primera ecuación:
$$ \begin{cases} x = \frac{5 - 2z}{3} \\ 2x - y + 3z = 5 \end{cases} $$
Sustituimos esta expresión de \( x \) en la segunda ecuación y resolvemos para \( y \):
$$ \begin{cases} x = \frac{5 - 2z}{3} \\ 2\left(\frac{5 - 2z}{3}\right) - y + 3z = 5 \end{cases} $$
$$ \begin{cases} x = \frac{5 - 2z}{3} \\ \frac{10 - 4z}{3} - y + 3z = 5 \end{cases} $$
Aislamos \( y \):
$$ y = \frac{10 - 4z}{3} - 5 + 3z $$
$$ y = \frac{10 - 4z - 15 + 9z}{3} $$
Simplificamos la expresión:
$$ y = \frac{5z -5}{3} $$
Por tanto, la forma bivariante queda:
$$ \begin{cases} x = \frac{5 -2z}{3} \\ \\ y = \frac{5z -5}{3} \end{cases} $$
Cualquier método algebraico puede emplearse para resolver el sistema; en este caso, sumar las ecuaciones resultó una estrategia cómoda.
Ecuaciones Fraccionarias y Paramétricas de una Recta
Dados dos puntos distintos $A(x_1, y_1, z_1)$ y $B(x_2, y_2, z_2)$, la recta que pasa por ellos puede expresarse mediante las siguientes ecuaciones fraccionarias: $$ \frac{x - x_1}{l} = \frac{y - y_1}{m} = \frac{z - z_1}{n} $$ donde: $$ l = x_2 - x_1, \quad m = y_2 - y_1, \quad n = z_2 - z_1 $$ Los valores $l, m, n$ se denominan cocientes directores de la recta.
Las ecuaciones fraccionarias constituyen una forma concisa de representar una recta en el espacio tridimensional, pues permiten describir en una única expresión cómo varían las coordenadas $x$, $y$ y $z$ a lo largo de la recta.
Sabemos que la condición para que tres puntos sean colineales en el espacio se expresa así:
$$ \frac{ x - x_1 }{ x_2 - x_1 } = \frac{ y - y_1 }{ y_2 - y_1 } = \frac{ z - z_1 }{ z_2 - z_1 } $$
Definimos los denominadores de esta igualdad como $ l = x_2 - x_1 $, $ m = y_2 - y_1 $ y $ n = z_2 - z_1 $.
$$ \frac{ x - x_1 }{ l } = \frac{ y - y_1 }{ m } = \frac{ z - z_1 }{ n } $$
Estas cantidades $l, m, n$ reciben el nombre de cocientes directores y expresan cuánto se desplaza cada coordenada en los ejes $x$, $y$ y $z$ al recorrer la recta de un punto a otro.
- $l = x_2 - x_1$ indica la variación en la coordenada $x$ desde $A$ hasta $B$.
- $m = y_2 - y_1$ indica la variación en el eje $y$.
- $n = z_2 - z_1$ indica la variación en el eje $z$.
En definitiva, los números $l, m, n$ describen la dirección en que se extiende la recta en el espacio en cada una de sus dimensiones.
En otras palabras, el vector $(l, m, n)$ es el vector director de la recta, pues determina su dirección y sentido en el espacio.
Nota. Si multiplicamos los cocientes directores por un mismo escalar distinto de cero $k$, la dirección de la recta no varía. Es decir, los vectores $(l, m, n)$ y $(k\,l, k\,m, k\,n)$ determinan la misma recta. Por tanto, dos rectas son paralelas si sus cocientes directores son proporcionales, es decir, si se cumple que $ l = k\,l' $, $ m = k\,m' $ y $ n = k\,n' $, lo que implica las siguientes proporciones: $$ \frac{l}{l'} = \frac{m}{m'} = \frac{n}{n'} = k $$
Ejemplo
Consideremos los puntos:
$$ A(1, -2, 3), \quad B(5, 4, 1) $$
Calculemos los cocientes directores:
$$ l = 5 - 1 = 4 $$
$$ m = 4 - (-2) = 6 $$
$$ n = 1 - 3 = -2 $$
Las ecuaciones fraccionarias de la recta que pasa por $A$ y $B$ son:
$$ \frac{x - 1}{4} = \frac{y + 2}{6} = \frac{z - 3}{-2} $$
Esta ecuación fraccionaria indica que por cada incremento de $l$ en $x$, se produce un incremento proporcional de $m$ en $y$ y una variación de $n$ en $z$.
Cada fracción señala cuántas veces se ha recorrido el vector director a partir del punto $A$.
En este caso, el vector director es $ \vec{v} = (4, 6, -2) $.
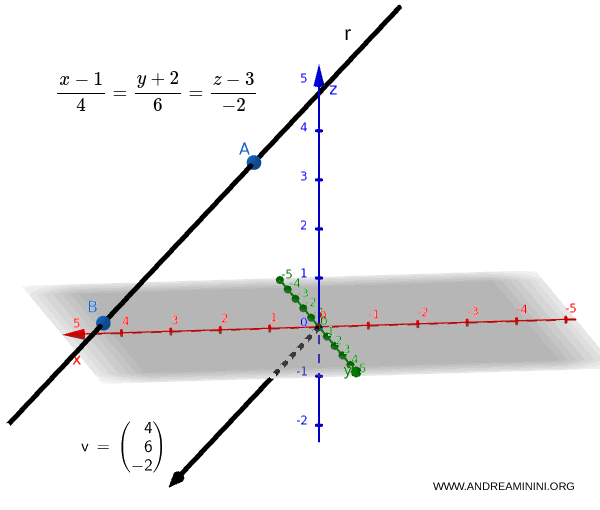
Casos con Coeficientes Nulos. Si alguno de los cocientes directores $l, m, n$ es igual a cero, significa que la recta es paralela a uno de los planos coordenados:
- Si $l = 0$, la recta es paralela al plano $Oyz$, por lo que $x$ permanece constante.
- Si $m = 0$, la recta es paralela al plano $Oxz$, por lo que $y$ permanece constante.
- Si $n = 0$, la recta es paralela al plano $Oxy$, por lo que $z$ permanece constante.
En estos casos, no pueden escribirse ecuaciones fraccionarias, ya que implicarían una división por cero. En su lugar, se emplean ecuaciones simplificadas que indican explícitamente la coordenada constante.
Ecuaciones Paramétricas
Si igualamos las tres fracciones a un mismo parámetro $t$, obtenemos el sistema:
$$ \begin{cases} \frac{x - x_1}{l} = t \\ \frac{y - y_1}{m} = t \\ \frac{z - z_1}{n} = t \end{cases} $$
Resolviendo cada ecuación para $x$, $y$ y $z$, se obtiene:
$$ \begin{cases} x - x_1 = l\,t \\ y - y_1 = m\,t \\ z - z_1 = n\,t \end{cases} $$
$$ \begin{cases} x = x_1 + l\,t \\ y = y_1 + m\,t \\ z = z_1 + n\,t \end{cases} $$
Estas se conocen como las ecuaciones paramétricas de la recta.
Por tanto, las ecuaciones fraccionarias pueden considerarse una forma alternativa de expresar las ecuaciones paramétricas.
Ejemplo
Tomemos la ecuación fraccionaria del ejemplo anterior:
$$ \frac{x - 1}{4} = \frac{y + 2}{6} = \frac{z - 3}{-2} $$
Podemos transformarla en un sistema, igualando todas las fracciones al parámetro $t$:
$$ \begin{cases} \frac{x - 1}{4} = t \\ \\ \frac{y + 2}{6} = t \\ \\ \frac{z - 3}{-2} = t \end{cases} $$
Despejando $x$, $y$ y $z$, se obtiene:
$$ \begin{cases} x = 1 + 4\,t \\ \\ y = -2 + 6\,t \\ \\ z = 3 - 2\,t \end{cases} $$
Estas son las ecuaciones paramétricas de la misma recta.
Coordenadas Polares de una Recta
- La ecuación de una recta también puede expresarse mediante coordenadas polares.
- Si la recta pasa por el origen, basta con conocer el ángulo α que determina su inclinación: $$ m = \tan \alpha,\quad \text{con}\quad \alpha \neq \frac{\pi}{2} + k\pi $$
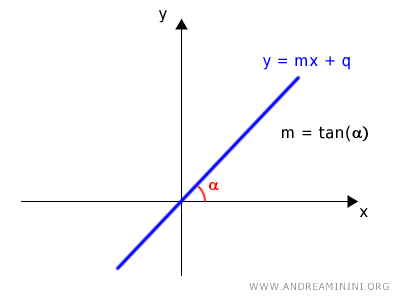
- Si la recta no pasa por el origen, es necesario conocer la distancia d entre la recta y el polo (origen) y el ángulo β que forma ese segmento con el eje polar positivo: $$ d = r \cdot \cos(\theta) $$
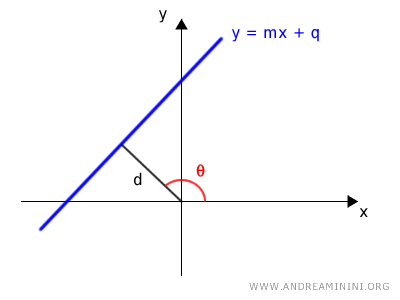
donde θ es el ángulo polar de cualquier punto P sobre la recta.
Observaciones
A continuación se presentan algunas consideraciones y notas sobre la ecuación lineal (la ecuación de la recta).
- La ecuación de una recta determina todos los puntos que pertenecen a esa recta
Esto puede demostrarse por reducción al absurdo. Supongamos que existe un punto P'(x, y') fuera de la recta r que satisface la ecuación lineal ax+by+c=0. Según esta hipótesis, P' tiene la misma abscisa que un punto P de la recta, pero distinta ordenada.
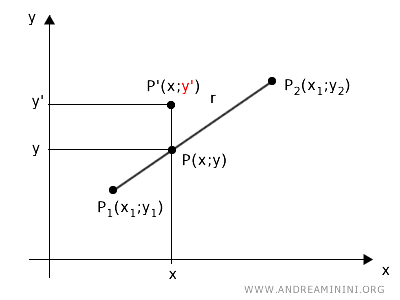
De acuerdo con esta suposición, se verifican simultáneamente las dos ecuaciones: $$ ax+by+c=0 $$ $$ ax+by'+c=0 $$ Para resolver este sistema, empleamos el método de reducción, restando la segunda ecuación de la primera: $$ \begin{matrix} ax & +by & +c &=0 & - \\ ax & +by' & +c &=0 \\ \hline 0 & +b(y - y') &0 &=0 \end{matrix} $$ Lo que conduce a: $$ b(y - y')=0 $$ Como b es distinto de cero, la única manera de que se cumpla esta igualdad es que y=y'. Es decir, el punto externo P' tendría la misma ordenada que P. Esto contradice nuestra hipótesis inicial de que P' está fuera de la recta. Por tanto, es falso que puntos ajenos a r satisfagan la ecuación ax+by+c=0. En consecuencia, únicamente los puntos de la recta cumplen dicha ecuación. - Toda ecuación lineal corresponde a una recta, y viceversa
Cualquier ecuación lineal en dos variables x e y define una recta en el plano cartesiano, y toda recta admite una ecuación de este tipo: $$ r \quad \Longleftrightarrow \quad ax+by+c=0 $$Demostración. Como los coeficientes "a" y "b" no pueden ser ambos nulos, consideremos dos casos extremos: a=0, b≠0 y a≠0, b=0. En el primer caso, obtenemos un haz de rectas paralelas al eje x; en el segundo, rectas paralelas al eje y.
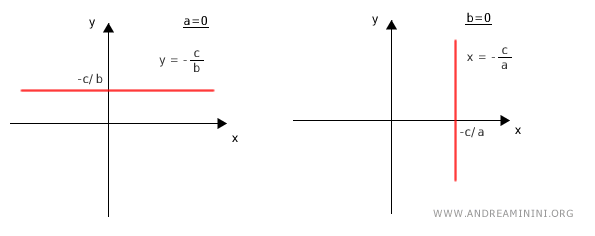
En el caso general, donde a≠0 y b≠0, la ecuación se mantiene en la forma ax+by+c=0. Debemos probar que esta ecuación corresponde a una única recta. Tomemos tres puntos de la recta, (x₁,y₁), (x₂,y₂) y (x₃,y₃), e impongamos: $$ \begin{cases} ax_1 + by_1 + c=0 \\ ax_2 + by_2 + c=0 \\ ax_3 + by_3 + c=0 \end{cases} $$ Si restamos la tercera ecuación de las dos primeras: $$ \begin{cases} a(x_1 - x_3) + b(y_1 - y_3)=0 \\ a(x_2 - x_3) + b(y_2 - y_3)=0 \end{cases} $$ Esto nos lleva a: $$ \frac{x_1 - x_3}{y_1 - y_3}= \frac{x_2 - x_3}{y_2 - y_3}= -\frac{b}{a} $$ Lo que corresponde a la condición de alineación de tres puntos: $$ \frac{x_1 - x_3}{x_2 - x_3}= \frac{y_1 - y_3}{y_2 - y_3} $$ Así, queda demostrado que la ecuación ax+by+c=0 describe una y solo una recta en el plano.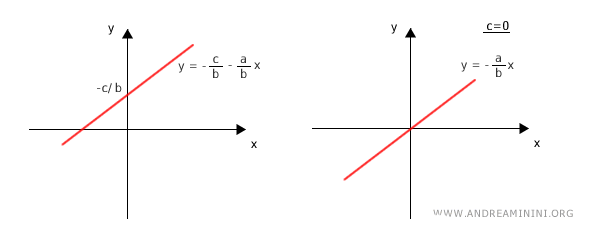
Y así sucesivamente.