Haz Propio de Rectas

Un haz de rectas (concurrente de rectas) es el conjunto de todas las rectas que pasan por un punto específico (A) en el plano, denominado centro del haz.

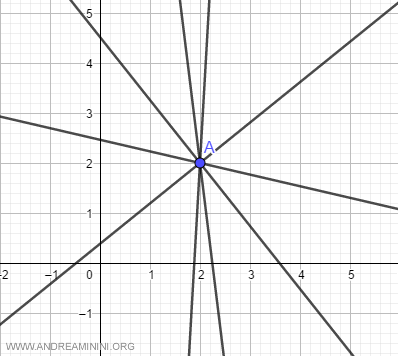
La ecuación de un haz de rectas con centro en un punto de coordenadas \((x_0, y_0)\) se expresa así:

$$ y - y_0 = m \cdot (x - x_0) $$

Esta ecuación describe todas las rectas del haz que pasan por el punto \( (x_0, y_0) \), cuando se hace variar la pendiente \( m \in \mathbb{R} \), excepto la recta paralela al eje y.

Nota. La recta paralela al eje y no puede expresarse con la ecuación explícita \( y = mx \), pues no existe ningún valor de \( m \) que la represente. En estos casos, se utiliza la ecuación: $$ x = x_0 $$

En general, dado un punto P con coordenadas $ (x_0, y_0) $, el haz de rectas centrado en P se define mediante el siguiente sistema:

$$
\begin{cases}
y - y_0 = m \cdot (x - x_0) & \text{si la recta no es paralela al eje y} \\
x = x_0 & \text{si la recta es paralela al eje y}
\end{cases}
$$

Al conjunto de todas las rectas que concurren en el centro del haz se lo denomina haz completo.

Otra forma de expresar las rectas del haz centrado en C es mediante la ecuación: $$ y - y_0 = -\frac{h}{k} \cdot (x - x_0) $$ donde h y k son enteros cualesquiera $ h,k \in \mathbb{Z} $ con k ≠ 0.

Ejemplo Práctico

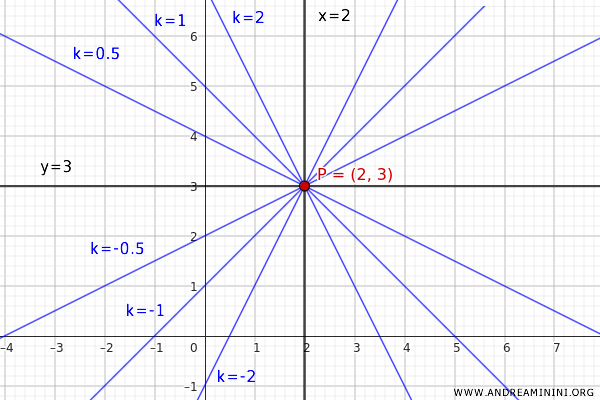
Consideremos el punto P(2,3) en el plano como centro del haz.

Utilizamos entonces las ecuaciones correspondientes al haz de rectas:

$$
\begin{cases}
y - y_0 = m \cdot (x - x_0) \\
x = x_0
\end{cases}
$$

En este caso, el centro del haz tiene coordenadas P(2,3), con x₀=2 e y₀=3

$$
\begin{cases}
y - 3 = m \cdot (x - 2) \\
x = 2
\end{cases}
$$

La ecuación \( y - 3 = m(x - 2) \) define un haz de rectas que pasan por el punto \( (2, 3) \). Este haz abarca todas las posibles rectas con diferentes pendientes \( m \), salvo la paralela al eje y.

La ecuación \( x = 2 \), representada en rojo, corresponde a la recta paralela al eje y que pasa por el punto \( (2, 3) \).

A continuación se muestran algunas rectas pertenecientes al haz completo centrado en P(2,3).

Ejemplo 2

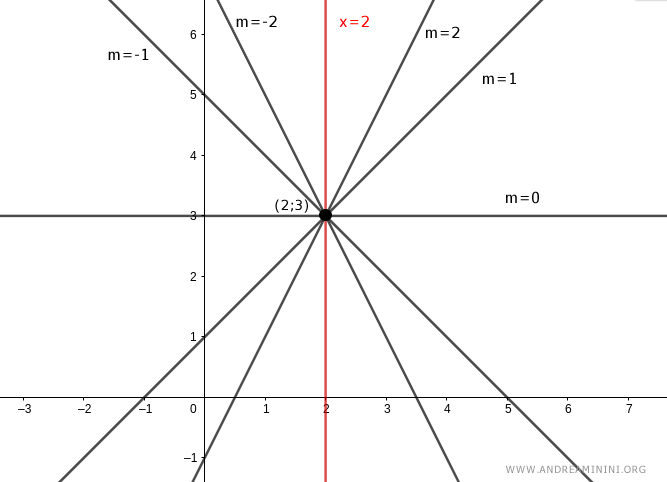
En este segundo ejemplo, tomamos el punto C:

$$ C = \begin{pmatrix} x_0 = 2 \\ y_0 = 3 \end{pmatrix} $$

Podemos describir las rectas del haz centrado en C con la siguiente ecuación:

$$ y - y_0 = -\frac{h}{k} \cdot (x - x_0) $$

donde h y k son enteros cualesquiera $ h,k \in \mathbb{Z} $ con k ≠ 0, para evitar el inconveniente de la división por cero.

$$ y - 3 = -\frac{h}{k} \cdot (x - 2) $$

Si despejamos y, obtenemos la ecuación explícita de la recta:

$$ y = -\frac{h}{k} \cdot (x - 2) + 3 $$

Cada combinación de h y k determina una recta que pasa por el punto C.

Así, para obtener el haz completo de rectas, basta con variar la razón h/k.

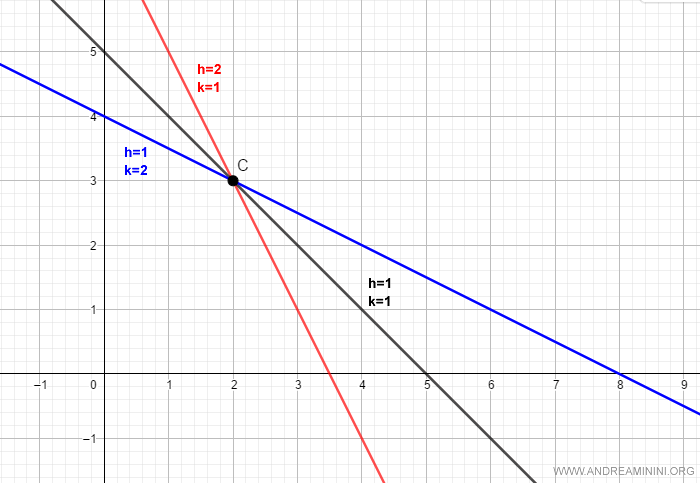
También en este caso, la recta paralela al eje y debe describirse con una ecuación distinta, que es $ x = x_0 $, en este caso, $ x = 2 $.

Demostración

Un haz de rectas tiene su centro en un punto P con coordenadas (x₀, y₀):

$$ P(x_0, y_0) $$

Cualquier recta perteneciente al haz debe pasar por el punto P(x₀, y₀):

$$ y = m x + q $$

Sustituimos y = y₀ y x = x₀:

$$ y_0 = m x_0 + q $$

Despejamos q:

$$ q = y_0 - m x_0 $$

Sustituimos q = y₀ - m x₀ en la ecuación general de la recta:

$$ y = m x + q $$

$$ y = m x + (y_0 - m x_0) $$

$$ y = m x + y_0 - m x_0 $$

Agrupamos términos para aislar las variables:

$$ y - y_0 = m x - m x_0 $$

$$ y - y_0 = m (x - x_0) $$

Esta es la ecuación final del haz de rectas.

Nota. Esta ecuación abarca todas las rectas del haz, salvo la paralela al eje y. Para dicha recta, es necesario utilizar la ecuación específica x = x₀.

Demostración Alternativa

Si el punto A en el plano tiene las coordenadas:

$$ A = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} $$

entonces la ecuación cartesiana de todas las rectas del haz es:

$$ h(x - x_0) + k(y - y_0) = 0 $$

donde h y k son coeficientes aún indeterminados.

Dividimos toda la ecuación entre k:

$$ \frac{h(x - x_0)}{k} + \frac{k(y - y_0)}{k} = 0 $$

$$ \frac{h(x - x_0)}{k} + y - y_0 = 0 $$

Reordenamos para aislar las variables:

$$ y - y_0 = -\frac{h}{k} \cdot (x - x_0) $$

La razón -h/k corresponde a la pendiente (m) de las rectas.

Si la sustituimos por m, obtenemos la ecuación del haz de rectas en su forma explícita:

$$ y - y_0 = m \cdot (x - x_0) $$

Cada recta del haz se determina por un valor específico de la pendiente m.

Nota. En el caso particular de una recta paralela al eje y (vertical), esta ecuación no es válida porque m no está definida. En dicho caso, la ecuación de la recta es x - x₀ = 0.

Generación de las Rectas de un Haz

Para construir un haz de rectas, se pueden tomar dos rectas secantes r y s, conocidas como las rectas generadoras del haz.

$$ ax + by + c = 0 $$

$$ a'x + b'y + c' = 0 $$

El haz de rectas se obtiene considerando todas las combinaciones lineales posibles de estas dos rectas:

$$ p \cdot (ax + by + c) + q \cdot (a'x + b'y + c') = 0 $$

donde p y q son números escalares.

Para simplificar la expresión, podemos dividir toda la ecuación entre p:

$$ \require{cancel} \frac{ \cancel{p} \cdot (ax + by + c)}{ \cancel{p} } + \frac{ q \cdot (a'x + b'y + c') }{ p } = \frac{0}{p} $$

$$ ax + by + c + \frac{q}{p} \cdot (a'x + b'y + c') = 0 $$

Suponemos que p es distinto de cero, p ≠ 0, para evitar divisiones por cero.

Definimos el parámetro $ k = \frac{q}{p} $ para una forma aún más sencilla:

$$ ax + by + c + k \cdot (a'x + b'y + c') = 0 $$

donde k es un número racional cualquiera, y cada valor de k determina una recta diferente en el haz.

Esta ecuación representa todas las rectas del haz, salvo la recta $ a'x + b'y + c' = 0 $, que no puede obtenerse directamente en esta forma porque requeriría que k tendiera a infinito.

Nota. La recta $ ax + by + c = 0 $ se obtiene fijando k = 0 o bien q/p = 0. En cambio, la recta $ a'x + b'y + c' = 0 $ no puede generarse en la forma $$ (ax + by + c) + k \cdot (a'x + b'y + c') = 0 $$ y solo se puede aproximar haciendo que k tienda a infinito, es decir, $ k \rightarrow \infty $. La única forma de obtener exactamente la recta $ a'x + b'y + c' = 0 $ es volver a la combinación lineal original y asignar p = 0 y q = 1: $$ p \cdot (ax + by + c) + q \cdot (a'x + b'y + c') = 0 $$

¿Qué Rectas Generadoras Elegir para Formar un Haz Centrado en P(x₀, y₀)?

Cualquier par de rectas secantes que pase por el punto P(x₀, y₀) es válido para generar el haz.

No obstante, para facilitar los cálculos, lo más práctico suele ser escoger rectas paralelas a los ejes cartesianos que pasen por P(x₀, y₀):

$$ y = y_0 $$

$$ x = x_0 $$

cuyas formas equivalentes son:

$$ y - y_0 = 0 $$

$$ x - x_0 = 0 $$

Así, la ecuación del haz se reduce a:

$$ p \cdot (y - y_0) + q \cdot (x - x_0) = 0 $$

$$ (y - y_0) + \frac{q}{p} \cdot (x - x_0) = 0 $$

Nota. El resultado final es equivalente a la fórmula de la ecuación de la recta que pasa por un punto con pendiente $ m = - \frac{q}{p} $: $$ y = m \cdot (x - x_0) + y_0 $$

¿Qué Recta del Haz Pasa por el Origen?

Para hallar el valor de \( k \) que genera una recta que pase por el origen O(0, 0), partimos de la ecuación del haz:

$$ (ax + by + c) + k \cdot (a'x + b'y + c') = 0 $$

Queremos que dicha recta pase por el punto x = 0, y = 0.

Sustituyamos estos valores en la ecuación:

$$ a \cdot 0 + b \cdot 0 + c + k \cdot (a' \cdot 0 + b' \cdot 0 + c') = 0 $$

$$ c + k \cdot c' = 0 $$

Despejando k, obtenemos:

$$ k \cdot c' = -c $$

$$ k = -\frac{c}{c'} $$

Este es el valor de \( k \) que determina la recta del haz que pasa por el origen, siempre que \( c' \neq 0 \) para evitar divisiones por cero.

Nota. Si \( c' = 0 \) y \( c \neq 0 \), no existe ningún valor finito de \( k \) que haga que la recta pase por el origen. Si tanto \( c \) como \( c' \) son cero, cualquier valor de \( k \) satisface la ecuación, lo cual significa que todas las rectas del haz pasan por el origen.

Ejemplo

Consideremos las siguientes rectas generadoras en el plano cartesiano:

$$ r:\ 2x + 3y + 4 = 0 $$

$$ s:\ x - 2y + 1 = 0 $$

Como son rectas secantes, pueden elegirse como rectas generadoras del haz.

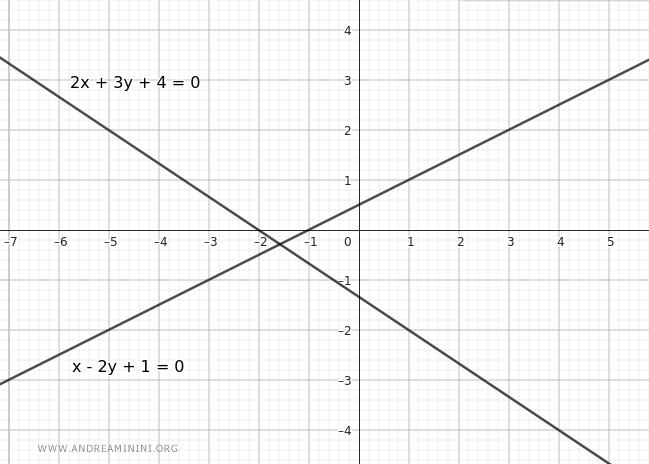
Utilizamos su combinación lineal para definir el haz:

$$ (2x + 3y + 4) + k \cdot (x - 2y + 1) = 0 $$

Desarrollamos y agrupamos términos semejantes:

$$ (2 + k) x + (3 - 2k) y + (4 + k) = 0 $$

Esta ecuación genera las rectas del haz a medida que varía el parámetro k, salvo la recta $ s:\ x - 2y + 1 = 0 $.

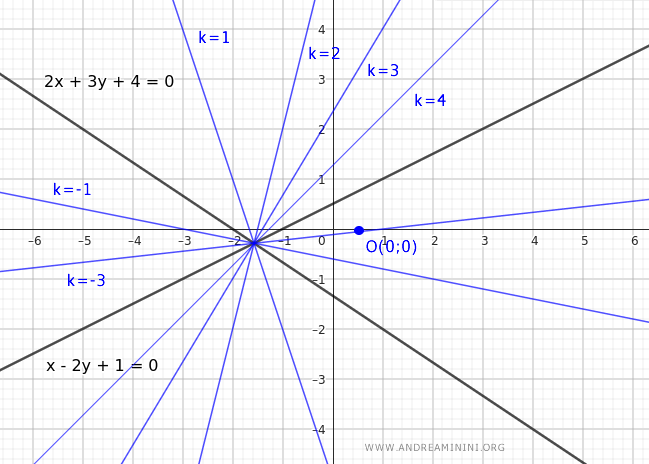
Nota. La recta $ s:\ x - 2y + 1 = 0 $ debe añadirse aparte al haz, ya que no se corresponde con ningún valor finito de k.

¿Cuál es la Ecuación de la Recta que Pasa por el Origen?

Para encontrar la recta del haz que pase por el origen, imponemos que la ecuación se cumpla para \( x = 0 \) y \( y = 0 \):

$$ (2 + k) \cdot 0 + (3 - 2k) \cdot 0 + (4 + k) = 0 $$

$$ 4 + k = 0 $$

Despejamos k y obtenemos:

$$ k = -4 $$

Sustituyamos k = -4 en la ecuación del haz para hallar la ecuación de la recta que pasa por el origen:

$$ (2 - 4) x + (3 + 8) y + (4 - 4) = 0 $$

$$ -2x + 11y = 0 $$

$$ y = \frac{2}{11} x $$

Esta es la ecuación de la recta del haz que pasa por el origen.

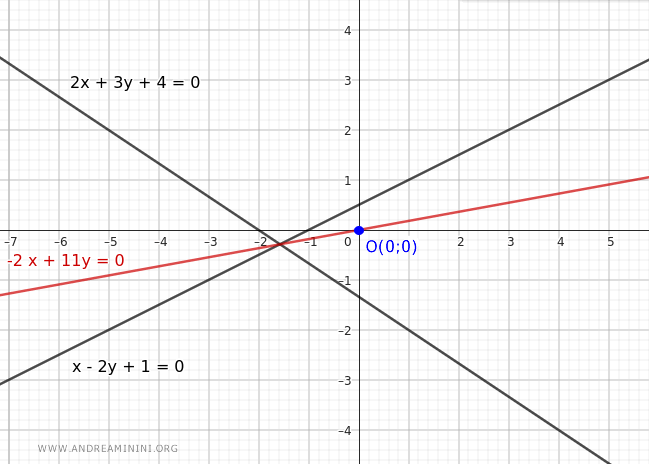
Ejemplo 2

En este ejemplo, queremos construir un haz de rectas centrado en un punto concreto, por ejemplo P(2, 3).

$$ P (2, 3) $$

Primero, escogemos dos rectas secantes que pasen por el punto P para usarlas como rectas generadoras del haz.

Podríamos elegir entre infinitas rectas, pero lo más sencillo es utilizar rectas paralelas a los ejes coordenados:

1. Una recta paralela al eje x que pase por \( (2, 3) \), cuya ecuación es \( y = 3 \) o bien $ y - 3 = 0 $.
2. Una recta paralela al eje y que pase por \( (2, 3) \), cuya ecuación es \( x = 2 \) o bien $ x - 2 = 0 $.

Estas dos rectas se cortan en el punto P(2, 3).

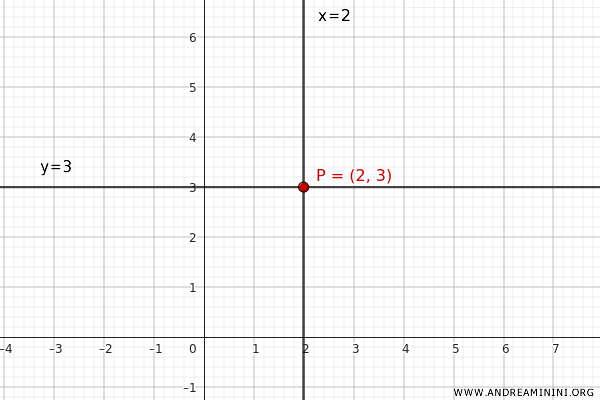
Sustituimos las dos ecuaciones $ y - 3 = 0 $ y $ x - 2 = 0 $ en la ecuación del haz:

$$ (ax + by + c) + k \cdot (a'x + b'y + c') = 0 $$

$$ (y - 3) + k \cdot (x - 2) = 0 $$

$$ y = - k \cdot (x - 2) + 3 $$

$$ y = - k x + 2k + 3 $$

donde k es la pendiente, que varía generando infinitas rectas que todas pasan por el punto P(2, 3).

Cada valor de k define una recta distinta dentro del haz.