Pendiente de una recta

La pendiente (también llamada coeficiente angular) de una recta en la forma $$ y = mx + b $$ representa la razón entre el cambio en las coordenadas y y el cambio en las coordenadas x entre dos puntos distintos de la recta: $$ m = \frac{y_B - y_A}{x_B - x_A} $$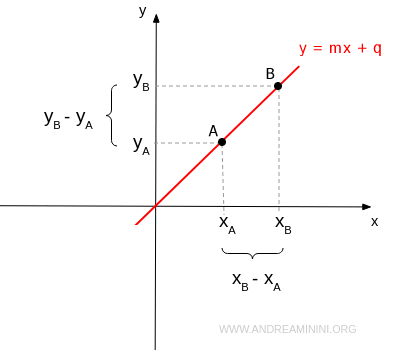

La pendiente mide la inclinación de la recta con respecto al eje x.

Es decir, indica el ángulo α que forma la recta con el eje x, donde el vértice está en el punto de intersección, y los lados son el semieje positivo del eje x y un segmento de la recta que tiene componente vertical positiva o nula.

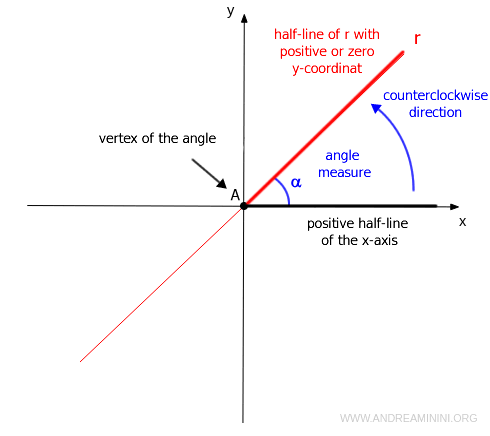
la pendiente mide el ángulo entre la recta y el eje x

Nota: Por convención, los ángulos se miden en sentido antihorario desde el eje x positivo.

Según la inclinación de la recta, la pendiente puede ser positiva, negativa o nula:

Pendiente positiva (m > 0): la recta es creciente y forma un ángulo agudo con el eje x.
Pendiente negativa (m < 0): la recta es decreciente y forma un ángulo obtuso con el eje x.
Pendiente nula (m = 0): la recta es constante, es decir, horizontal. Es paralela (o coincide) con el eje x y no forma ningún ángulo con él.

Nota: No se puede definir la pendiente de una recta vertical, es decir, paralela al eje y. caso de una recta vertical
Esto se debe a que el cálculo implica una división entre cero: $$ m = \frac{y_B - y_A}{x_B - x_A} = \frac{y_B - y_A}{0} $$ Una división por cero no está definida, ya que cualquier número multiplicado por cero siempre da cero, y por tanto no existe un valor que verifique la igualdad $ y = m \cdot 0 $.

Pendiente y tangente del ángulo

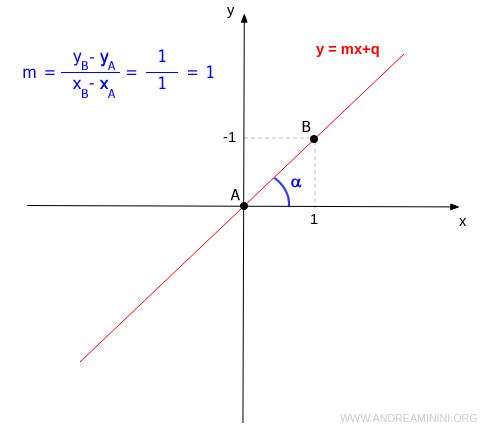
La pendiente $ m $ de una recta es igual a la tangente del ángulo $ \alpha $ que forma con el eje x: $$ m = \tan \alpha $$

Esta relación permite expresar la inclinación de la recta en términos trigonométricos.

Es especialmente útil cuando se desea calcular el ángulo $ \alpha $ conociendo la pendiente, o viceversa:

$$ m = \tan \alpha $$

$$ \alpha = \text{arctan}(m) $$

donde arctan es la función inversa de la tangente.

Nota: Esta fórmula requiere conocimientos previos de trigonometría y de cálculo diferencial. Por ello, suele introducirse a partir del último año de bachillerato o en cursos universitarios. La demostración se desarrolla en otra sección de este sitio.

Ejemplo

Sea la recta $ y = 2x - 1 $, cuya pendiente es $ m = 2 $.

ejemplo de una recta

¿Cuál es el ángulo $ \alpha $ que forma con el eje x?

Buscamos el ángulo cuya tangente es igual a 2:

$$ \tan \alpha = 2 $$

Aplicamos la función arco-tangente:

$$ \alpha = \text{arctan}(2) $$

Esto da como resultado:

$$ \alpha_{\text{rad}} \approx 1.107 \, \text{rad} $$

Convertimos este valor a grados: $$ \alpha = 1.107 \cdot \frac{180^\circ}{\pi} \approx 63.43^\circ $$

Por lo tanto, la recta forma un ángulo de aproximadamente 63.43° con el eje x.

ángulo medido en grados

Hemos determinado así el ángulo $ \alpha $ a partir de la pendiente.

Y así sucesivamente.