Rectas
¿Qué es una recta?
Una recta es un trayecto rectilíneo e ilimitado, formado por puntos, que se extiende indefinidamente en ambas direcciones sin desviarse ni curvarse en ningún momento.
La recta constituye uno de los elementos fundamentales de la geometría euclidiana.
Según el primer postulado de Euclides, por cualesquiera dos puntos distintos pasa una y solo una recta.
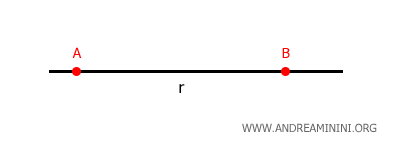
Por convención, las rectas suelen representarse mediante letras minúsculas, mientras que los puntos se denotan con letras mayúsculas.
Nota. De este postulado se desprende que una recta no puede curvarse: dados dos pares de puntos distintos en el plano (A, B) y (B, C), todos pertenecen a la misma recta únicamente si se encuentran alineados.
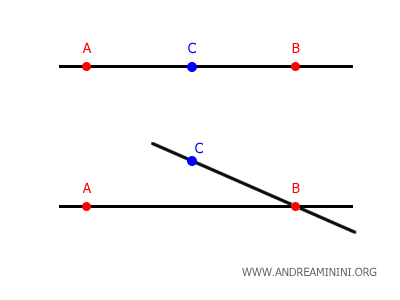
Según el segundo postulado de Euclides, una recta es un segmento que puede prolongarse indefinidamente en ambas direcciones.

Por tanto, una recta no posee ni origen ni fin.
Nota. Esta es la diferencia esencial entre una recta y un segmento, ya que este último sí cuenta con dos extremos: un punto inicial y otro final.
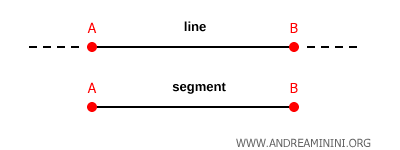
Dados dos puntos cualesquiera sobre una recta, siempre es posible encontrar al menos un punto intermedio entre ellos.
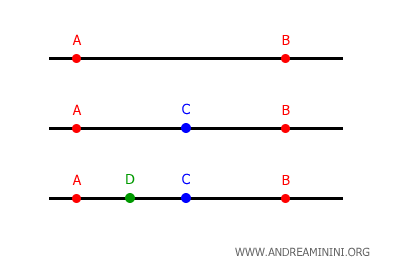
Por este motivo, se dice que la recta constituye un conjunto denso.
Nota. Existe una correspondencia biunívoca entre los puntos de una recta y el conjunto de los números reales: ambos son conjuntos infinitos con la misma densidad.
Muchas propiedades de las rectas derivan directamente de los dos primeros postulados de Euclides.
Cuando dos o más rectas pasan por un mismo punto, se denominan rectas concurrentes o secantes.
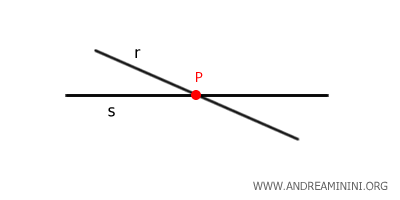
Por un mismo punto pueden pasar infinitas rectas.
El conjunto de todas las rectas que pasan por un punto recibe el nombre de haz de rectas.
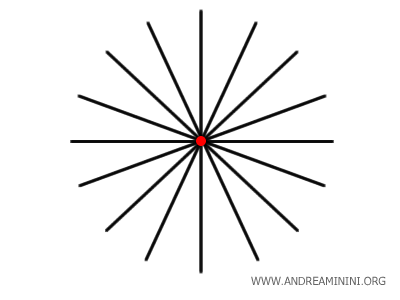
Nota. Como una recta está formada por un conjunto de puntos, contiene necesariamente al menos un punto. Para definirla, son necesarios al menos dos puntos distintos; de ahí que por cualquier punto del plano puedan pasar infinitas rectas distintas.
Dado que un plano contiene infinitos puntos, también contiene infinitas rectas.
Para definir un plano es necesario, como mínimo, un conjunto de tres puntos no alineados.
En el espacio tridimensional, una recta puede definirse como la intersección de dos planos.
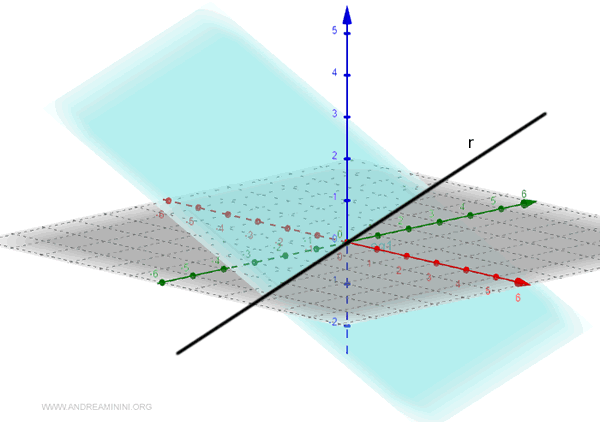
Nota. Esta definición es una simplificación de un concepto más general que se extiende a espacios de mayor dimensión en matemáticas avanzadas.
Sobre cualquier recta es posible establecer un sentido o dirección.
Una recta a la que se asigna una dirección se denomina recta orientada.
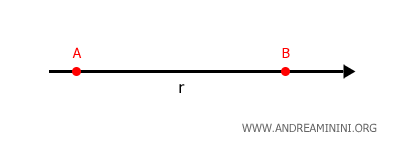
En el plano cartesiano, una recta se representa mediante una ecuación lineal:
$$ y = mx + b $$
donde:
- "y" es la coordenada vertical de cualquier punto de la recta,
- "x" es la coordenada horizontal de cualquier punto de la recta,
- "m" es la pendiente de la recta, que determina su inclinación: m = Δy / Δx,
- "b" es la ordenada en el origen, es decir, el valor de y cuando x = 0 (el punto de corte con el eje Y).
Gráficamente, la ecuación de la recta en el plano cartesiano se representa así:
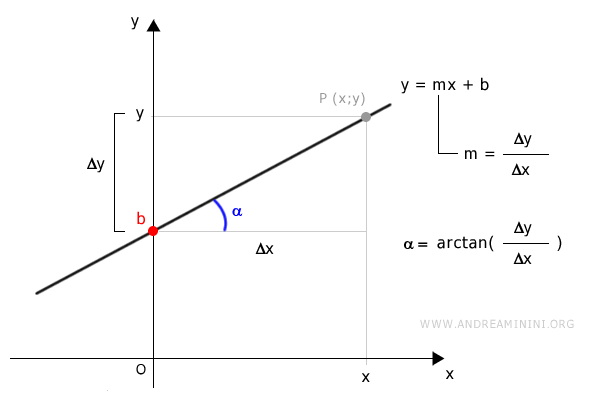
Dados dos puntos sobre una recta, siempre es posible determinar su ecuación aplicando la fórmula de la pendiente y la ecuación general de la recta.
Y así sucesivamente.