Los postulados de Euclides
En su obra fundamental "Los Elementos", Euclides formuló cinco postulados que constituyen los cimientos de la geometría euclidiana.
Estos cinco postulados son afirmaciones fundamentales que se aceptan como verdaderas sin necesidad de demostración.
Sobre estos postulados se construye la geometría plana, que forma parte del currículo básico de matemáticas en la enseñanza escolar.
Nota: Si se rechaza tan solo uno de estos postulados, se genera una geometría distinta, conocida como geometría no euclidiana.
Los postulados son los siguientes:
Primer postulado
Por dos puntos cualesquiera puede trazarse una recta que los una.

Este postulado garantiza la existencia y unicidad de la recta: por dos puntos distintos pasa una única recta.
Corolarios
De este principio se derivan varios corolarios importantes:
- Por un mismo punto pueden trazarse infinitas rectas.
- Por toda recta pasan al menos dos puntos.
- Por tres puntos no alineados pasa un único plano.
- Por tres puntos alineados pasa una única recta.
- Por una recta dada pueden pasar infinitos planos.
Segundo postulado
Un segmento de recta puede prolongarse indefinidamente en línea recta.

Tercer postulado
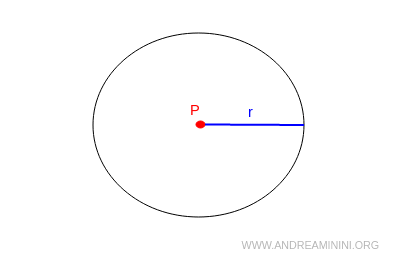
Dado un punto y un segmento de longitud determinada, es posible trazar una circunferencia con centro en el punto y radio igual a la longitud del segmento.
Cuarto postulado
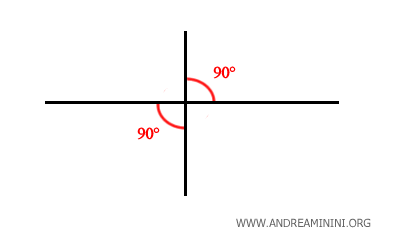
Todos los ángulos rectos son congruentes, es decir, tienen la misma medida.
Quinto postulado
Si una recta "r" corta a otras dos rectas "s" y "t", de modo que la suma de los ángulos interiores α y β situados en el mismo lado de "r" sea menor que dos ángulos rectos (α + β < 180°), entonces las rectas "s" y "t", si se prolongan indefinidamente, se cortarán en un punto P.
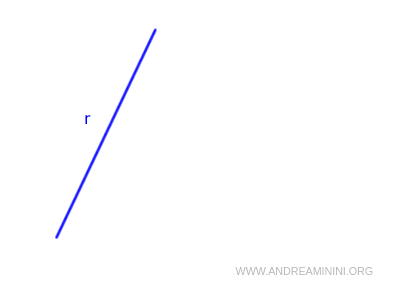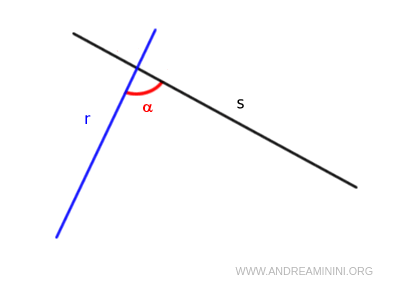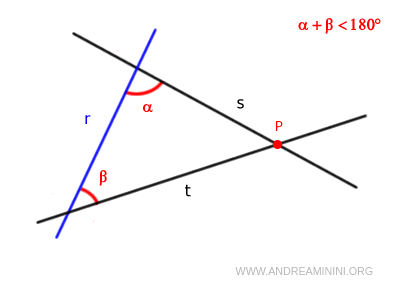
Este quinto postulado de Euclides también es conocido como el postulado de las paralelas.
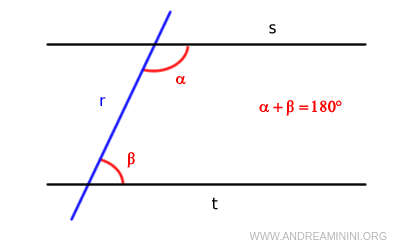
Ello se debe a que, si una recta corta a otras dos de tal manera que la suma de los ángulos interiores es exactamente 180°, entonces esas dos rectas son paralelas y no se cortarán en el plano.
A lo largo de la historia, este postulado ha sido reformulado de diversas maneras equivalentes.
Nota: El quinto postulado de Euclides ha sido objeto de profundas reflexiones y debates durante siglos. Durante más de dos mil años, los matemáticos intentaron deducirlo a partir de los otros cuatro postulados, sin éxito. No fue hasta el siglo XIX cuando se demostró que esto no era posible. Al modificar el quinto postulado se obtiene una geometría distinta de la euclidiana: la geometría no euclidiana. Entre sus principales variantes se encuentran la geometría esférica, la geometría hiperbólica y la geometría elíptica.
Y así sucesivamente.