Ecuación de la Circunferencia en Forma Polar
La forma polar de la ecuación de una circunferencia se expresa como: $$ r^2 + r_c^2 - 2 \cdot r \cdot r_c \cos (\alpha - \alpha_c) - R^2 = 0 $$ donde \( R \) es el radio de la circunferencia, y \( r_c \) y \( r \) representan las distancias desde el origen (polo) hasta el centro \( C \) y hasta un punto cualquiera \( P \) sobre la circunferencia, respectivamente.
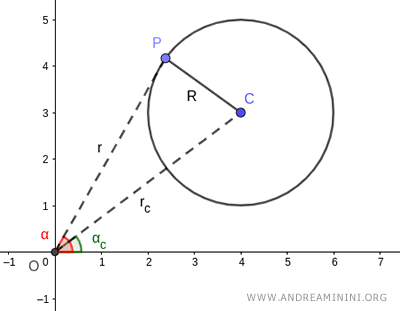
Variando las coordenadas polares (α, r), se pueden determinar todos los puntos que pertenecen a la circunferencia.
En esta ecuación, el ángulo α y la distancia r son las variables.
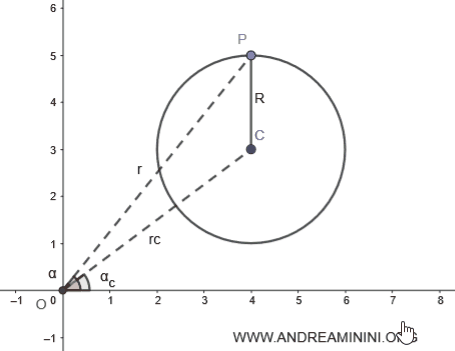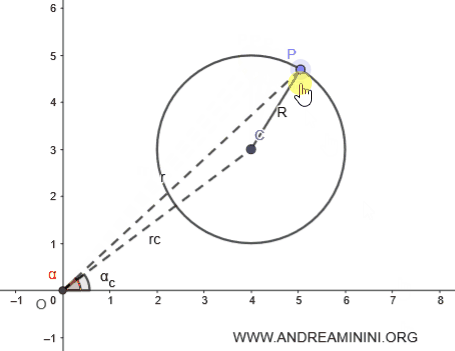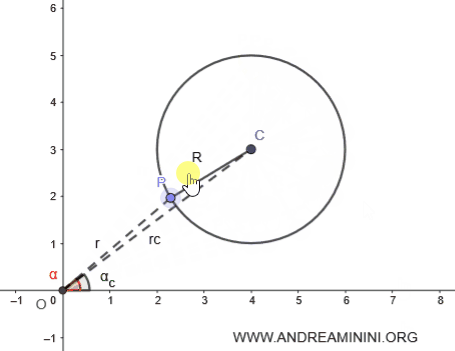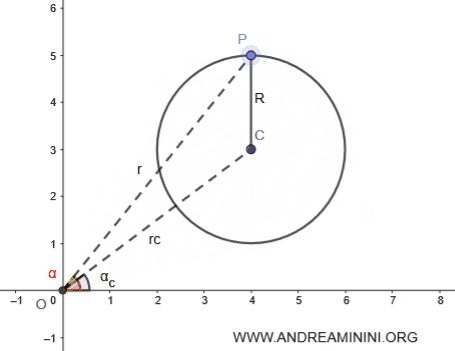
Demostración
Consideremos una circunferencia cualquiera en el plano.
Supongamos que la circunferencia tiene un radio \( R = 2 \).
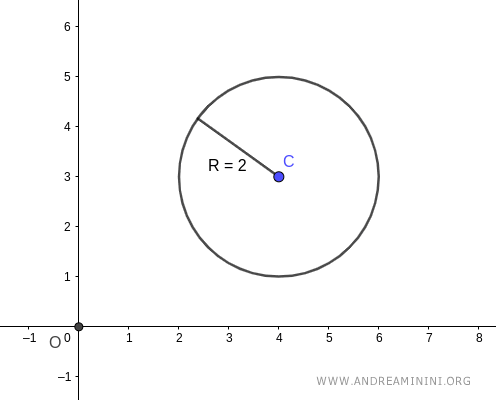
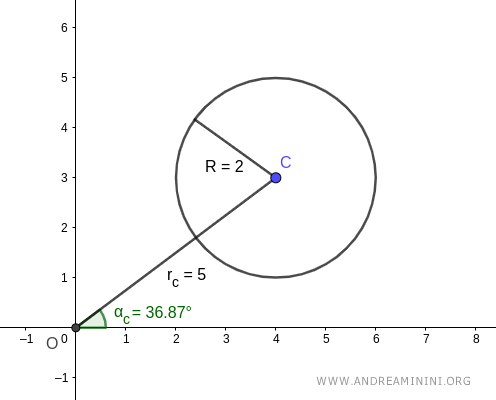
El centro de la circunferencia \( C \) se encuentra en las coordenadas polares (\(\alpha_c\), \(r_c\)):
$$ C: (\alpha_c, r_c) = (36.87^\circ, 5) $$
Es decir, el ángulo \(\alpha_c\) es 36.87° y la distancia \( r_c \) es 5.
Ahora, consideremos un punto cualquiera \( P \) sobre la circunferencia:
$$ P: (\alpha, r) = (60.27^\circ, 4.8) $$
El punto \( P \) tiene coordenadas polares \(\alpha = 60.27^\circ\) y \( r = 4.8 \).
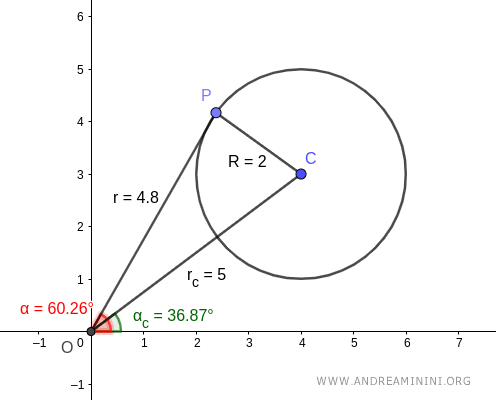
El radio \( R \), junto con los segmentos \( OP \) y \( OC \), forma el triángulo \( OPC \).
Aplicando la ley de los cosenos en el triángulo \( OPC \), obtenemos:
$$ \overline{PC}^2 = \overline{OP}^2 + \overline{OC}^2 - 2 \cdot \overline{OP} \cdot \overline{OC} \cdot \cos(\alpha - \alpha_c) $$
Como los lados del triángulo son \( PC = R \), \( OC = r_c \) y \( OP = r \), resulta:
$$ R^2 = r^2 + r_c^2 - 2 \cdot r \cdot r_c \cdot \cos(\alpha - \alpha_c) $$
Reordenando los términos, llegamos a:
$$ r^2 + r_c^2 - 2 \cdot r \cdot r_c \cdot \cos(\alpha - \alpha_c) - R^2 = 0 $$
Esta es la ecuación de la circunferencia en coordenadas polares, lo que completa la demostración.
Verificación: Sustituyamos los valores \(\alpha = 60.27^\circ\), \(\alpha_c = 36.87^\circ\), \( r = 4.8 \), \( r_c = 5 \) y \( R = 2 \) en la ecuación: $$ R^2 = r^2 + r_c^2 - 2 \cdot r \cdot r_c \cdot \cos(\alpha - \alpha_c) $$ $$ 2^2 = 4.8^2 + 5^2 - 2 \cdot 4.8 \cdot 5 \cdot \cos(60.27^\circ - 36.87^\circ) $$ $$ 4 = 23.04 + 25 - 2 \cdot 24 \cdot \cos(23.4^\circ) $$ $$ 4 = 48.04 - 44 $$ $$ 4 ≈ 4 $$ Lo cual confirma que la ecuación es correcta.
Y así sucesivamente.