Potencia de un Punto respecto a una Circunferencia

La potencia de un punto \( P(x,y) \) respecto a una circunferencia \( (x - a)^2 + (y - b)^2 = r^2 \) se define como la diferencia entre el cuadrado de la distancia del punto al centro \( C(a,b) \) de la circunferencia y el cuadrado del radio. $$ \pi(P) = d^2 - r^2 $$

Dado que la distancia \( d \) entre dos puntos se calcula mediante la fórmula:

$$ d = \sqrt{(x - a)^2 + (y - b)^2} $$

La potencia del punto respecto a la circunferencia se puede expresar así:

$$ \pi(P) = (x - a)^2 + (y - b)^2 - r^2 $$

Este valor mide la «distancia relativa» del punto con respecto a la circunferencia.

Nota: No mide la distancia euclídea directa del punto a la circunferencia, ya que tiene en cuenta también el radio.

El signo de la potencia indica la posición del punto \( P \) con respecto a la circunferencia:

• Si \(\pi(P) > 0\), el punto está en el exterior de la circunferencia.
• Si \(\pi(P) = 0\), el punto está sobre la circunferencia.
• Si \(\pi(P) < 0\), el punto está en el interior de la circunferencia.

Ejemplo Práctico

Consideremos el punto \( P(6,3) \) y una circunferencia con centro en \( C(3,3) \) y radio \( r = 2 \).

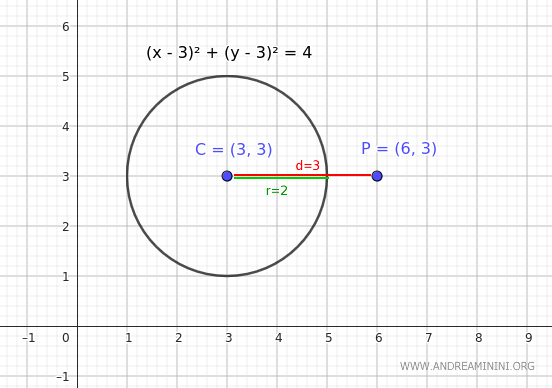
La distancia del punto \( P \) al centro \( C \) de la circunferencia se calcula fácilmente y resulta ser 3.

$$ d = \sqrt{(6 - 3)^2 + (3 - 3)^2} = \sqrt{3^2} $$

$$ d = 3 $$

Por tanto, la potencia del punto \( P \) respecto a la circunferencia se obtiene restando los cuadrados de la distancia y del radio:

$$ \pi(P) = d^2 - r^2 $$

$$ \pi(P) = 3^2 - 2^2 $$

$$ \pi(P) = 9 - 4 $$

$$ \pi(P) = 5 $$

En este caso, la potencia del punto es 5.

Ejemplo 2

Consideremos ahora el punto \( P(7,6) \) y la misma circunferencia del ejemplo anterior, con centro \( C(3,3) \) y radio \( r = 2 \).

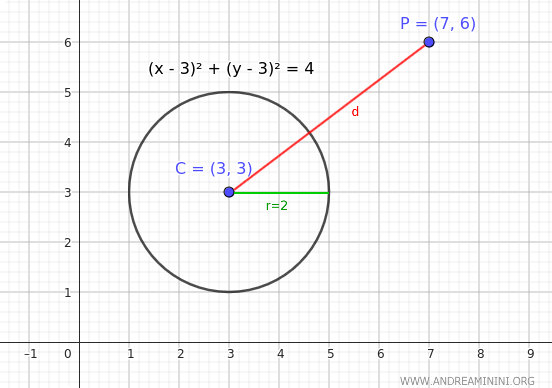
En este caso, el punto está más alejado que en el ejemplo anterior, pero el radio de la circunferencia sigue siendo el mismo.

Calculemos la distancia entre el centro de la circunferencia y el punto \( P \):

$$ d = \sqrt{(x - a)^2 + (y - b)^2} $$

$$ d = \sqrt{(7 - 3)^2 + (6 - 3)^2} $$

$$ d = \sqrt{4^2 + 3^2} $$

$$ d = \sqrt{16 + 9} $$

$$ d = \sqrt{25} $$

$$ d = 5 $$

Sabiendo que el radio de la circunferencia es \( r = 2 \), calculamos la potencia del punto \( P \) respecto a la circunferencia:

$$ \pi(P) = d^2 - r^2 $$

$$ \pi(P) = 5^2 - 2^2 $$

$$ \pi(P) = 25 - 4 $$

$$ \pi(P) = 21 $$

Por tanto, la potencia del punto respecto a la circunferencia es 21.

Observaciones

Algunas observaciones adicionales sobre la potencia de un punto respecto a una circunferencia:

• Un punto \( P \) con la misma potencia respecto a dos circunferencias se encuentra sobre el eje radical
  Si consideramos dos circunferencias con centros \( C_1 \) y \( C_2 \) y radios \( r_1 \) y \( r_2 \), un punto \( P \) que tiene la misma potencia respecto a ambas satisface la ecuación: \[ (x - x_1)^2 + (y - y_1)^2 - r_1^2 = (x - x_2)^2 + (y - y_2)^2 - r_2^2 \] Este punto se encuentra sobre una recta llamada «eje radical», donde las potencias respecto a las dos circunferencias son iguales, sin depender de las distancias físicas.
• Un punto \( P \) sobre el eje radical suele estar más cerca del centro de la circunferencia de menor radio
  Esto se deduce fácilmente de la ecuación: \[ (x - x_1)^2 + (y - y_1)^2 - r_1^2 = (x - x_2)^2 + (y - y_2)^2 - r_2^2 \] Si uno de los radios es menor, la distancia entre el punto y el centro de esa circunferencia debe ser también menor para mantener la igualdad y que la potencia sea la misma respecto a la otra circunferencia. $$ \pi_1(P) = \pi_2(P) $$ $$ (x - x_1)^2 + (y - y_1)^2 - r_1^2 = (x - x_2)^2 + (y - y_2)^2 - r_2^2 $$ $$ \pi_1(P) = \pi_2(P) $$ $$ (x - x_1)^2 + (y - y_1)^2 - [r_1^2 - \Delta r + \Delta r] = (x - x_2)^2 + (y - y_2)^2 - r_2^2 $$ $$ (x - x_1)^2 + (y - y_1)^2 - \Delta r - [r_1^2 - \Delta r] = (x - x_2)^2 + (y - y_2)^2 - r_2^2 $$ $$ \left[(x - x_1)^2 + (y - y_1)^2 - \Delta r\right] - [r_1^2 - \Delta r] = (x - x_2)^2 + (y - y_2)^2 - r_2^2 $$

Ejemplo. Consideremos una circunferencia con centro en \( C(3,3) \) y radio \( r = 2 \), y el punto \( P(6,3) \). Ya calculamos previamente que la potencia de este punto respecto a la circunferencia es \( \pi(P) = 5 \). Para encontrar otra circunferencia con la misma potencia pero con radio \( r = 1 \), utilizamos la fórmula de la potencia: $$ \pi(P) = d^2 - r^2 $$ En este caso, sabemos que \( \pi = 5 \) y que el radio de la nueva circunferencia es \( r = 1 \): $$ 5 = d^2 - 1^2 $$ Por tanto, la nueva circunferencia debe encontrarse a una distancia de \(\sqrt{6} \approx 2,4495\) del punto \( P \): $$ d^2 = 5 + 1 $$ $$ d = \sqrt{6} $$ En conclusión, la nueva circunferencia, al tener un radio menor, debe estar también más cerca para que la potencia se mantenga constante.

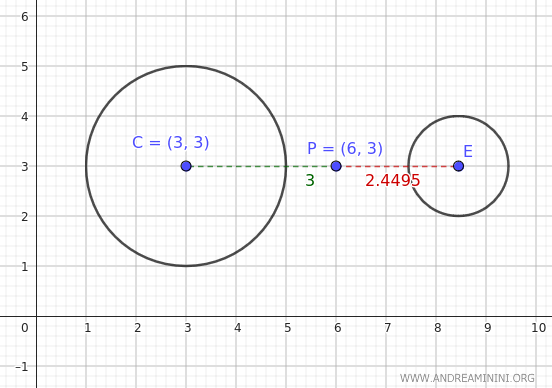
Como verificación final, calculamos la potencia del punto \( P(6,3) \) respecto a la nueva circunferencia de radio \( r = 1 \) y distancia \( d = \sqrt{6} \). Su centro se situaría, por ejemplo, en \( E(6 + \sqrt{6}, 3) \). $$ \pi(P) = d^2 - r^2 $$ $$ \pi(P) = (\sqrt{6})^2 - 1^2 $$ $$ \pi(P) = 6 - 1 $$ $$ \pi(P) = 5 $$ Así, el punto \( P \) mantiene la misma potencia \( \pi(P) = 5 \) respecto a la nueva circunferencia.

Y así sucesivamente.