Ciclotomía (Geometría)
La ciclotomía es un problema geométrico que consiste en dividir una circunferencia en n partes iguales utilizando únicamente regla y compás.
Este desafío, de origen griego, es conocido también como el problema de la construcción de polígonos regulares.
Si es posible dividir una circunferencia en n partes iguales con instrumentos elementales, entonces es igualmente factible construir un polígono regular de n lados. Un caso clásico es el hexágono.
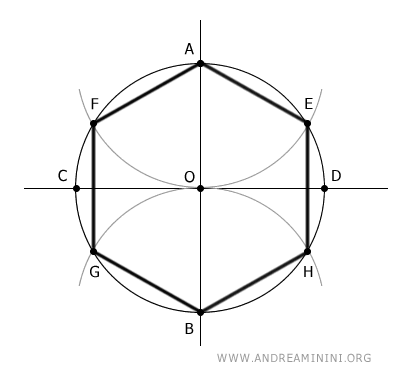
Los filósofos y matemáticos griegos aspiraban a comprender el mundo natural mediante formas geométricas puras, aunque no lograron resolver de manera general el problema de la ciclotomía.
Los matemáticos griegos consiguieron construir polígonos regulares de 3 (triángulo) a 6 (hexágono) lados, pero el polígono regular de 7 lados se les resistió. A pesar de siglos de esfuerzos por parte de numerosos matemáticos, la construcción de un heptágono regular permaneció irresoluta durante más de dos mil años, hasta que Gauss demostró en el siglo XIX que tal construcción es imposible con los métodos clásicos.
Condiciones de Gauss para la ciclotomía
En el siglo XIX, Carl Friedrich Gauss logró, finalmente, resolver el problema de la ciclotomía.
Gauss estableció que una circunferencia puede dividirse en partes iguales mediante regla y compás si, y solo si, se cumplen ciertas condiciones:
- n es un número primo de la forma:
$$ n = 2^{2^k} + 1 $$
Aquí, \( k \) es un número natural (k∈N), y estos valores se conocen como números de Fermat. - n no es primo, sino producto de una potencia de 2 y de primos de Fermat distintos:
$$ n = 2^m \cdot p_1 \cdot p_2 \cdot ... \cdot p_n $$
Donde \( m \) es un número natural (m∈N), y cada \( p_i \) es 1 o bien un número de Fermat \( 2^{2^k}+1 \), siempre que sean primos y entre sí distintos.
Este descubrimiento permitió a Gauss dar una solución definitiva al problema de la ciclotomía.
Las condiciones de Gauss excluyen la posibilidad de dividir una circunferencia en partes iguales cuando n es un número primo que no responde a la forma de Fermat (como 7, 11, 13, etc.) o cuando es un número compuesto que no cumple la segunda condición. En consecuencia, no es posible construir un polígono regular con ese número de lados utilizando únicamente regla y compás.
Ejemplo
Según el criterio de Gauss, es posible dividir una circunferencia en partes como 3, 5, 17 (primos de Fermat), así como en 4, 8, 16 (potencias de dos), o combinaciones como 15 (3 × 5), 10 (2 × 5), etc.
Por el contrario, la regla de Gauss excluye la construcción de polígonos regulares con, por ejemplo, 7, 9, 11, 13, 14, etc., lados.
Verificación. Los números de Fermat son los siguientes:
| $ k $ | $ 2^{2^k} + 1 $ |
| 0 | 21+1=3 |
| 1 | 22+1=5 |
| 2 | 24+1=17 |
| 3 | 28+1=257 |
| 4 | 216+1=65537 |
De la primera condición de Gauss se deduce que, seleccionando primos de Fermat, se puede dividir la circunferencia en 3, 5, 17, 257 o 65537 partes.
$$ n = \ 3 \ , \ 5 \ , \ 17 \ , \ 257 \ , \ ... $$
Cabe destacar que no todos los números de Fermat son primos; únicamente los cinco primeros son conocidos por ser primos. Es fundamental escoger únicamente aquellos que realmente lo sean.
De acuerdo con la segunda condición de Gauss, también se consideran números \( n \) no primos, que surgen al multiplicar potencias de dos (2m = 1, 2, 4, 8, … con m≥0) por primos de Fermat distintos (3, 5, 17, …).
$$ 2^0 \cdot 3 \cdot 5 = 15 \\ 2^0 \cdot 3 \cdot 17 = 51 \\ \vdots $$
Así, combinando todos estos números, es posible dividir una circunferencia en n partes, donde n puede ser 3, 4, 5, 6, 8, 10, 12, 15, 16, 17, … empleando solo regla y compás.
Sin embargo, dividir una circunferencia en 7, 9, 11, 13, 14, … partes sigue siendo imposible con esos instrumentos, lo cual implica igualmente que no se pueden construir polígonos regulares de siete, nueve, etc., lados utilizando únicamente regla y compás.
Observaciones
Algunas consideraciones adicionales:
- Los hallazgos de Gauss no solo resolvieron un antiguo problema geométrico, sino que abrieron nuevas vías en la teoría de números, el álgebra y las matemáticas discretas. La ciclotomía está íntimamente ligada a la teoría de campos ciclotómicos y a las ecuaciones polinómicas, y posee implicaciones relevantes en criptografía y teoría de la información. Hoy en día, la ciclotomía actúa como un puente entre la geometría clásica y la teoría moderna de números, demostrando cómo antiguos problemas pueden desembocar en descubrimientos profundos que trascienden siglos.
En esencia, la simple cuestión de cómo dividir una circunferencia ha ampliado nuestro conocimiento sobre la simetría, la factorización de números y la estructura algebraica de los polinomios, sentando las bases para futuros avances en diversas áreas de las matemáticas.
Y así sucesivamente.