Recta Tangente a una Circunferencia

Se denomina recta tangente a una circunferencia a aquella que la toca en un único punto.

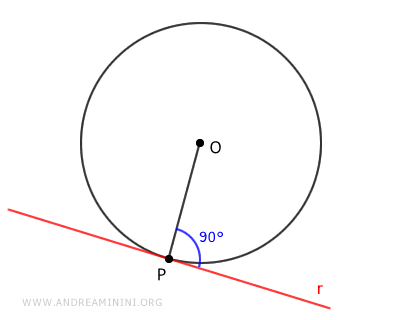
En otras palabras, una tangente solo tiene un punto de contacto con la circunferencia.

Esto contrasta claramente con las rectas secantes, que intersectan la circunferencia en dos puntos, y con las rectas exteriores, que no llegan a cortarla en ningún punto.

Nota: Según el teorema de intersección entre una recta y una circunferencia, una recta puede cortar a una circunferencia, como máximo, en dos puntos.

Unicidad de la Tangente en un Punto de la Circunferencia

Por cada punto P situado sobre la circunferencia, existe una única recta tangente.

Este teorema refleja un principio fundamental: en cualquier punto P de la circunferencia, solo puede existir una única recta tangente.

Demostración

Consideremos una circunferencia de centro O y radio OP. Pensemos en una recta (r) que sea tangente a la circunferencia exactamente en el punto P.

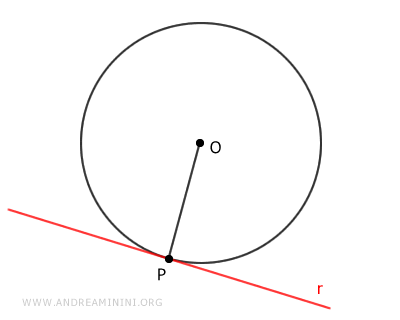
Por definición, la recta tangente solo intersecta la circunferencia en ese único punto.

Sabemos que por un punto exterior a una recta solo se puede trazar una perpendicular. Por tanto, se deduce que la tangente en el punto P solo puede admitir una perpendicular trazada desde el centro O.

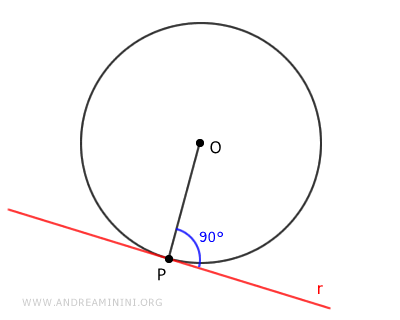
De acuerdo con el teorema sobre la distancia de una recta al centro de una circunferencia, si una recta es tangente en un punto de la circunferencia, la distancia d(r,O) desde el centro (O) hasta la recta es igual al radio (OP).

$$ d(r,O) \cong \overline{OP} $$

Nota: Cuando hablamos de la «distancia» entre una recta (r) y un punto (O), nos referimos al segmento más corto que los une, es decir, el perpendicular. Cualquier otro segmento que no sea perpendicular sería más largo.

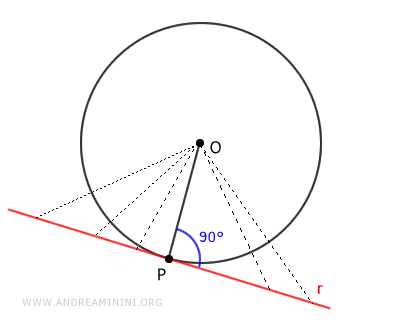
Dado que la distancia entre un punto y una recta siempre es perpendicular a esta, se concluye que el radio es perpendicular a la tangente en el punto P.

$$ \overline{OP} \perp r $$

Y dado que por P no pueden pasar dos rectas distintas perpendiculares a r, queda demostrado que en cada punto P de la circunferencia, solo puede existir una única recta tangente.

Cálculo de la Ecuación de la Tangente que Pasa por un Punto

En geometría analítica, para hallar la ecuación de una tangente que pase por un punto P(x₀, y₀), situado sobre la circunferencia o en el exterior, se plantea un sistema de ecuaciones:

$$ \begin{cases} x^2 + y^2 + ax + by + c = 0 \\ \\ y - y_0 = m (x - x_0) \end{cases} $$

La primera ecuación representa la circunferencia.

La segunda ecuación corresponde a una recta que pasa por el punto P(x₀, y₀).

Procedemos a despejar y en la ecuación de la recta y sustituimos en la ecuación de la circunferencia:

$$ \begin{cases} x^2 + [m(x - x_0) + y_0]^2 + ax + b[m(x - x_0) + y_0] + c = 0 \\ \\ y = m(x - x_0) + y_0 \end{cases} $$

Después, resolvemos la ecuación obtenida respecto a la pendiente m, imponiendo la condición Δ = 0, conocida como la condición de tangencia.

$$ \Delta = b^2 - 4ac $$

Aquí, a, b y c son los coeficientes de la ecuación cuadrática resultante.

Nota: La condición de tangencia b² - 4ac = 0 asegura que la recta toque a la circunferencia en un único punto, confirmando que se trata efectivamente de una tangente. Si no se cumple, la recta corta la circunferencia en dos puntos o no la toca en absoluto.

Al resolver para «m», pueden darse dos casos:

• Si el punto P(x₀, y₀) está sobre la circunferencia, existirá un único valor para la pendiente m, que determina la tangente única.
• Si el punto P(x₀, y₀) se encuentra fuera de la circunferencia, existirán dos valores, m₁ y m₂, pues desde un punto exterior se pueden trazar dos tangentes a la circunferencia.

Ejemplo

Consideremos la circunferencia definida por la ecuación cuadrática:

$$ x^2 + y^2 - 6x - 4y + 9 = 0 $$

Queremos hallar las rectas tangentes que pasan por el punto P(9, 0).

Primero debemos comprobar si el punto pertenece a la circunferencia.

Planteamos el sistema con la ecuación de la circunferencia y la ecuación general de la recta:

$$ \begin{cases} x^2 + y^2 - 6x - 4y + 9 = 0 \\ \\ y - y_0 = m(x - x_0) \end{cases} $$

Como la recta pasa por P(9, 0), sustituimos x₀ = 9 y y₀ = 0:

$$ \begin{cases} x^2 + y^2 - 6x - 4y + 9 = 0 \\ \\ y = m(x - 9) \end{cases} $$

Despejamos y en la ecuación de la recta y sustituimos en la ecuación de la circunferencia:

$$ \begin{cases} x^2 + (mx - 9m)^2 - 6x - 4(mx - 9m) + 9 = 0 \\ \\ y = m(x - 9) \end{cases} $$

$$ \begin{cases} x^2 + m^2x^2 - 18m^2x + 81m^2 - 6x - 4mx + 36m + 9 = 0 \\ \\ y = m(x - 9) \end{cases} $$

Reordenamos la ecuación cuadrática en su forma estándar:

$$ \begin{cases} x^2(1 + m^2) + x(-18m^2 - 6 - 4m) + 81m^2 + 36m + 9 = 0 \\ \\ y = m(x - 9) \end{cases} $$

Aplicamos la condición de tangencia, igualando el discriminante de la ecuación a cero:

$$ \Delta = b^2 - 4ac = 0 $$

En este caso, los coeficientes de la ecuación cuadrática son a = 1 + m², b = -18m² - 6 - 4m, y c = 81m² + 36m + 9.

$$ \Delta = (-18m^2 - 6 - 4m)^2 - 4(1 + m^2)(81m^2 + 36m + 9) $$

$$ \Delta = (-18m^2 - 6 - 4m)^2 - 4(1 + m^2)(81m^2 + 36m + 9) $$

$$ \Delta = 324m^4 + 144m^3 + 232m^2 + 48m + 36 - 4(81m^4 + 36m^3 + 90m^2 + 36m + 9) $$

$$ \Delta = 324m^4 + 144m^3 + 232m^2 + 48m + 36 - 324m^4 - 144m^3 - 360m^2 - 144m - 36 $$

$$ \Delta = -128m^2 - 96m $$

Resolvemos la ecuación del discriminante:

$$ \Delta = m(-128m - 96) $$

$$ \Delta = 32m(-4m - 3) $$

Las soluciones son:

$$ m = 0 $$

$$ -4m - 3 = 0 $$

Por tanto:

$$ m = 0 $$

$$ m = -\frac{3}{4} $$

Las pendientes de las rectas tangentes que pasan por el punto P(9, 0) son:

$$ m_1 = 0 $$

$$ m_2 = -\frac{3}{4} $$

Procedemos a hallar las ecuaciones de dichas tangentes.

Para \(m = 0\):

$$ y = 0 $$

Para \(m = -\frac{3}{4}\):

$$ y = -\frac{3}{4}(x - 9) $$

$$ y = -\frac{3}{4}x + \frac{3 \cdot 9}{4} $$

$$ y = -\frac{3}{4}x + \frac{27}{4} $$

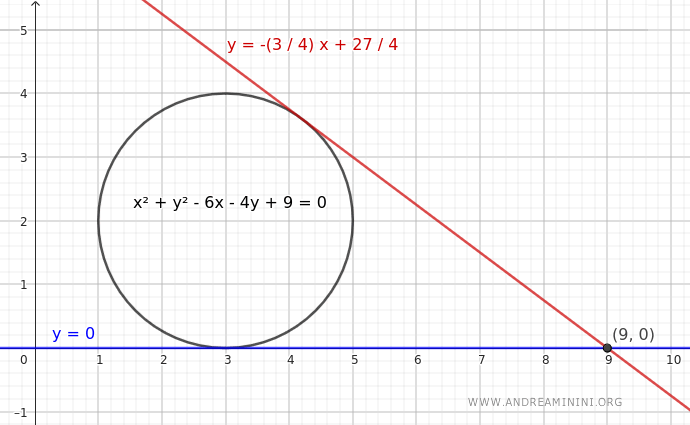
Por tanto, las ecuaciones de las rectas tangentes a la circunferencia que pasan por el punto P(9, 0) son:

$$ y = 0 $$

$$ y = -\frac{3}{4}x + \frac{27}{4} $$

Estas son las rectas tangentes a la circunferencia que pasan por el punto P(9, 0).

Métodos Alternativos para Hallar las Ecuaciones de las Tangentes

Existen varios métodos adicionales para determinar las ecuaciones de las rectas tangentes a una circunferencia.

• Método Basado en la Distancia entre la Recta y el Centro de la Circunferencia
• Método de la Tangente Perpendicular al Radio
• Método de la Fórmula de la Tangente

Método Basado en la Distancia entre la Recta y el Centro de la Circunferencia

Este método se fundamenta en conocer las coordenadas del centro de la circunferencia C y la longitud de su radio r.

Primero se escribe la ecuación de la familia de rectas que pasan por un punto P(x₀, y₀), que puede estar situado sobre la circunferencia o en el exterior de ella.

$$ y - y_0 = m(x-x_0) $$

Después, se determina cuál de esas rectas tiene una distancia al centro de la circunferencia C(x_c, y_c) exactamente igual al radio r. A partir de esa condición se obtiene el valor de la pendiente m.

$$ d = \frac{|ax_c + by_c + c|}{\sqrt{a^2 + b^2}} = r $$

Las rectas que cumplen esta igualdad son precisamente las tangentes a la circunferencia.

Ejemplo

Consideremos el punto P(9, 0) y la siguiente circunferencia:

$$ x^2 + y^2 - 6x - 4y + 9 = 0 $$

Primero calculamos las coordenadas del centro de la circunferencia, sabiendo que a = -6 y b = -4:

$$ (x_0, y_0) = \left(-\frac{a}{2}, -\frac{b}{2}\right) $$

$$ (x_0, y_0) = \left(-\frac{-6}{2}, -\frac{-4}{2}\right) $$

$$ (x_0, y_0) = \left( 3, 2 \right) $$

Para calcular el radio r, usamos la fórmula que relaciona los coeficientes de la ecuación de la circunferencia, siendo a = -6, b = -4 y c = 9:

$$ r = \sqrt{\left(-\frac{a}{2}\right)^2 + \left(-\frac{b}{2}\right)^2 - c} $$

$$ r = \sqrt{\left(-\frac{-6}{2}\right)^2 + \left(-\frac{-4}{2}\right)^2 - 9} $$

$$ r = \sqrt{3^2 + 2^2 - 9} $$

$$ r = \sqrt{9 + 4 - 9} $$

$$ r = \sqrt{4} $$

$$ r = 2 $$

Por tanto, el centro de la circunferencia está en C(3, 2) y el radio mide r = 2.

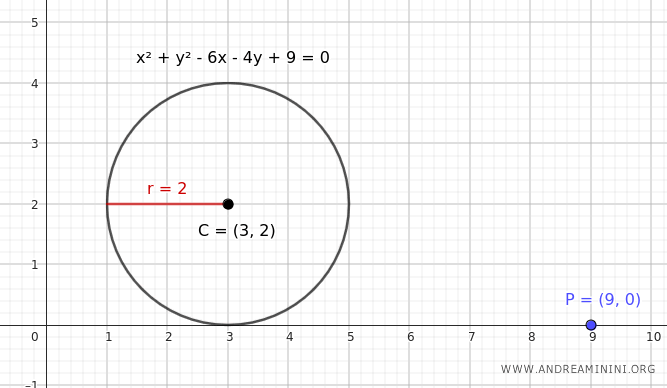
Escribimos ahora la ecuación de la familia de rectas que pasan por el punto P(x₀, y₀) = (9, 0):

$$ y - y_0 = m(x-x_0) $$

$$ y - 0 = m(x-9) $$

$$ y = mx - 9m $$

Llevamos esta ecuación a su forma general ax + by + c = 0. En este caso, a = m, b = -1 y c = -9m:

$$ mx - y - 9m = 0 $$

Buscamos las rectas cuya distancia al centro C(3, 2) sea igual al radio r = 2. Sabemos que las coordenadas del centro son x_c = 3 y y_c = 2, y que los coeficientes de la recta son a = m, b = -1 y c = -9m.

$$ d = \frac{|ax_c + by_c + c|}{\sqrt{a^2 + b^2}} = r $$

$$ \frac{|m \cdot 3 - 1 \cdot 2 - 9m|}{\sqrt{m^2 + 1}} = 2 $$

$$ \frac{|3m - 2 - 9m|}{\sqrt{m^2 + 1}} = 2 $$

$$ \frac{|-6m - 2|}{\sqrt{m^2 + 1}} = 2 $$

$$ |-6m - 2| = 2 \cdot \sqrt{m^2 + 1} $$

Elevamos ambos lados al cuadrado:

$$ (|-6m - 2|)^2 = \bigl(2 \cdot \sqrt{m^2 + 1}\bigr)^2 $$

$$ (6m + 2)^2 = 4(m^2 + 1) $$

$$ 36m^2 + 24m + 4 = 4m^2 + 4 $$

$$ 36m^2 + 24m + 4 - 4m^2 - 4 = 0 $$

$$ 32m^2 + 24m = 0 $$

Factorizamos m en lugar de resolver la ecuación cuadrática directamente:

$$ m \cdot (32m + 24) = 0 $$

La primera solución es inmediata: m = 0.

$$ m_1 = 0 $$

La segunda se obtiene resolviendo 32m + 24 = 0, lo que nos da m = -3/4:

$$ m_2 = -\frac{24}{32} = -\frac{3}{4} $$

Finalmente, sustituimos m₁ = 0 y m₂ = -3/4 en la ecuación de la familia de rectas:

$$ y = mx - 9m $$

Para m₁ = 0, obtenemos una de las rectas tangentes: y = 0

$$ y = mx - 9m = 0 \cdot x - 9 \cdot 0 = 0 $$

Para m₂ = -3/4, obtenemos la otra tangente: y = -(3/4)x + 27/4

$$ y = mx - 9m = -\frac{3}{4} \cdot x - 9 \cdot \left(-\frac{3}{4}\right) = -\frac{3}{4}x + \frac{27}{4} $$

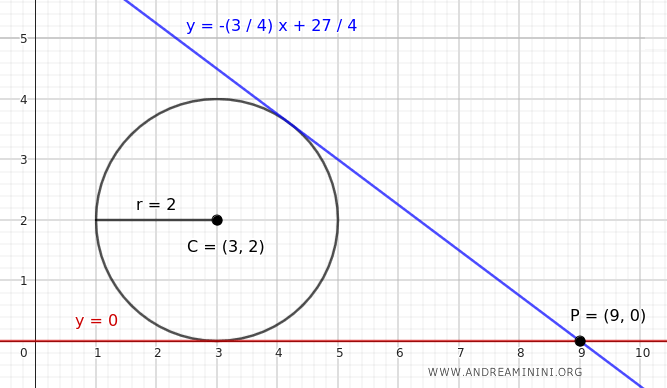
En este ejemplo, como P(9, 0) es un punto exterior a la circunferencia, existen dos rectas tangentes que pasan por él.

 

 

Método de la Tangente Perpendicular al Radio

Este método se basa en el principio de que la tangente en un punto P de la circunferencia es siempre perpendicular al radio en dicho punto, según el teorema de perpendicularidad entre radio y tangente.

Se sabe que, si dos rectas son perpendiculares, el producto de sus pendientes es igual a -1:

$$ m_r \cdot m_t = -1 $$

De ahí se obtiene una relación directa entre ambas pendientes:

$$ m_t = - \frac{1}{m_r} $$

Una vez determinada la ecuación de la recta que contiene el radio $ y = m_r x + q $, hallar la ecuación de la tangente es inmediato.

Basta con emplear el inverso negativo de la pendiente en la ecuación de la familia de rectas que pasan por el punto de tangencia P(x₀, y₀):

$$ y-y_0 = m_t \cdot (x-x_0) $$

Nota: Este método solo es válido si el punto P está sobre la circunferencia. No se aplica si P es un punto exterior.

Ejemplo

Consideremos una circunferencia definida por la ecuación:

$$ x^2 + y^2 - 4x - 4y - 2 = 0 $$

Queremos hallar la recta tangente en el punto P(5, 1) de la circunferencia.

$$ P(5, 1) $$

En primer lugar, calculamos el centro de la circunferencia, sabiendo que en su ecuación a = -4 y b = -4:

$$ (x_0, y_0) = \left(-\frac{a}{2}, -\frac{b}{2}\right) $$

$$ (x_0, y_0) = \left(-\frac{-4}{2}, -\frac{-4}{2}\right) $$

$$ (x_0, y_0) = \left( 2, 2 \right) $$

Por tanto, el centro C de la circunferencia está en (x, y) = (2, 2):

$$ C(2, 2) $$

Conocido el centro C(2, 2) y el punto de tangencia P(5, 1), hallamos la ecuación de la recta que pasa por ambos puntos, que es precisamente la recta que contiene el radio de la circunferencia.

$$ \frac{y - y_c}{y_t - y_c} = \frac{x - x_c}{x_t - x_c} $$

Las coordenadas del centro C son (x_c, y_c) = (2, 2), mientras que las del punto de tangencia P son (x_t, y_t) = (5, 1):

$$ \frac{y - 2}{1 - 2} = \frac{x - 2}{5 - 2} $$

$$ \frac{y - 2}{-1} = \frac{x - 2}{3} $$

$$ y - 2 = - \frac{x - 2}{3} $$

$$ y = - \frac{x - 2}{3} + 2 $$

$$ y = - \frac{x}{3} + \frac{2}{3} + 2 $$

$$ y = - \frac{x}{3} + \frac{8}{3} $$

Así, la pendiente de la recta que contiene el radio es m_r = -1/3:

$$ m_r = - \frac{1}{3} $$

Como la tangente en el punto P es perpendicular al radio y el producto de sus pendientes es igual a -1, deducimos que la pendiente de la tangente es m_t = 3:

$$ m_t = - \frac{1}{m_r} $$

$$ m_t = - \frac{1}{ - \frac{1}{3} } $$

$$ m_t = 3 $$

Ahora hallamos la ecuación de la tangente en el punto P(5, 1).

Para ello, utilizamos la ecuación de la familia de rectas que pasan por un punto:

$$ y - y_0 = m \cdot (x - x_0) $$

Sustituimos las coordenadas (x₀, y₀) por las del punto P(5, 1):

$$ y - 1 = m \cdot (x - 5) $$

Como la pendiente de la tangente es m_t = 3, obtenemos:

$$ y - 1 = 3 \cdot (x - 5) $$

$$ y = 3x - 15 + 1 $$

$$ y = 3x - 14 $$

Hemos hallado así la ecuación de la recta tangente en el punto P.

Método de la Fórmula de la Tangente

Para determinar la ecuación de la recta tangente en un punto P(x₀, y₀) de una circunferencia, puede emplearse la llamada fórmula de la tangente:

$$ xx_0 + yy_0 + a \frac{x + x_0}{2} + b \frac{y + y_0}{2} + c = 0 $$

Esta expresión permite obtener de forma directa la ecuación de la tangente.

Sin embargo, solo es aplicable si P es un punto situado sobre la circunferencia; no sirve si P se encuentra en el exterior.

Ejemplo

Consideremos la misma circunferencia del ejemplo anterior:

$$ x^2 + y^2 - 4x - 4y - 2 = 0 $$

Queremos hallar la ecuación de la recta tangente en el punto P(5, 1) perteneciente a dicha circunferencia.

$$ P(5, 1) $$

En este caso, aplicamos directamente la fórmula de la tangente:

$$ xx_0 + yy_0 + a \frac{x + x_0}{2} + b \frac{y + y_0}{2} + c = 0 $$

$$ xx_0 + yy_0 + \frac{a}{2}(x + x_0) + \frac{b}{2}(y + y_0) + c = 0 $$

Para la circunferencia \( x^2 + y^2 - 4x - 4y - 2 = 0 \), los coeficientes son:

 \( a = -4 \)
 \( b = -4 \)
 \( c = -2 \)

Sustituimos los valores \( a = -4 \), \( b = -4 \) y \( c = -2 \) en la fórmula:

$$ xx_0 + yy_0 + \frac{-4}{2}(x + x_0) + \frac{-4}{2}(y + y_0) - 2 = 0 $$

Las coordenadas del punto de tangencia P(5, 1) son \( x_0 = 5 \) y \( y_0 = 1 \).

$$ x \cdot 5 + y \cdot 1 + \frac{-4}{2}(x + 5) + \frac{-4}{2}(y + 1) - 2 = 0 $$

$$ 5x + y - 2(x + 5) - 2(y + 1) - 2 = 0 $$

$$ 5x + y - 2x - 10 - 2y - 2 - 2 = 0 $$

$$ 3x - y - 14 = 0 $$

Por tanto, la ecuación correcta de la recta tangente es:

$$ 3x - y - 14 = 0 $$

Hemos obtenido así la ecuación general de la recta tangente.

Para hallar la pendiente de la recta, despejamos y:

$$ y = 3x - 14 $$

Por lo tanto, la pendiente de la tangente es \( m = 3 \).

Y así sucesivamente.