La ecuación de la circunferencia

La ecuación estándar de una circunferencia en el plano cartesiano se expresa así: $$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$ donde \((x_0, y_0)\) son las coordenadas del centro \(O\) de la circunferencia y \(r\) es su radio.

Otra manera de escribir la ecuación de la circunferencia es en su forma general:

$$ x^2 + y^2 + ax + by + c = 0 $$

Los coeficientes están relacionados con el centro y el radio de la circunferencia mediante las siguientes expresiones:

$$ a = -2x_0 $$

$$ b = -2y_0 $$

$$ c = x_0^2 + y_0^2 - r^2 $$

Para hallar las coordenadas del centro \(O\) a partir de la ecuación general, se utiliza la fórmula del centro de la circunferencia:

$$ (x_0, y_0) = \left(-\frac{a}{2}, -\frac{b}{2}\right) $$

El radio \(r\) se determina aplicando la fórmula del radio, basada en la distancia euclídea entre el centro y cualquier punto de la circunferencia:

$$ r = \sqrt{\left(-\frac{a}{2}\right)^2 + \left(-\frac{b}{2}\right)^2 - c} $$

Es fundamental tener en cuenta que, para que \(x^2 + y^2 + ax + by + c = 0\) represente realmente una circunferencia, debe cumplirse la siguiente condición:

$$ \left(-\frac{a}{2}\right)^2 + \left(-\frac{b}{2}\right)^2 - c \geq 0 $$

Esta condición asegura que el valor bajo la raíz cuadrada sea no negativo, ya que el radio \(r\), por ser una longitud, no puede ser negativo.

Asimismo, es posible expresar la ecuación de la circunferencia de forma explícita en función de \(y\):

$$ y = y_0 \pm \sqrt{r^2 - (x - x_0)^2} $$

Esto  indica que, para determinados valores de \(x\), existen dos posibles valores de \(y\) (uno superior y otro inferior), salvo en el caso en que el radicando sea cero, situación en la que la circunferencia se reduce a un único punto (circunferencia degenerada, cuando \(r = 0\)).

Un ejemplo práctico

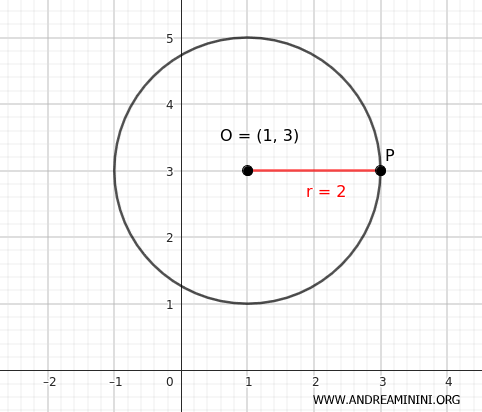
Veamos cómo construir una circunferencia cuyo centro esté en el punto \( (x, y) = (1, 3) \) y tenga radio \( r = 2 \).

La ecuación canónica de una circunferencia con estas características se obtiene a partir de la siguiente expresión:

$$  (x - x_0)^2 + (y - y_0)^2 = r^2 $$

Si sustituimos los valores x₀=1, y₀=3 y r=2, obtenemos:

$$  (x - 1)^2 + (y - 3)^2 = 2^2 $$

$$ (x - 1)^2 + (y - 3)^2 = 4 $$

Esta ecuación representa el conjunto de todos los puntos del plano que se encuentran exactamente a 2 unidades de distancia del centro \( (1, 3) \), describiendo así una circunferencia.

La demostración

Consideremos una circunferencia de radio "r" y centro O(x₀, y₀).

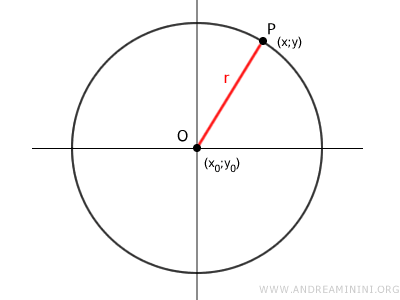
Un punto cualquiera P(x;y) del plano pertenece a la circunferencia si, y solo si, está a una distancia igual al radio r respecto del centro O.

$$ \overline{OP} = r $$

Elevamos al cuadrado ambos miembros de la igualdad:

$$ \overline{OP}^2 = r^2 $$

La longitud del segmento OP coincide con la distancia entre los puntos O y P, que se calcula aplicando el teorema de Pitágoras.

$$ \overline{OP} = \sqrt{ (x-x_0)^2 + (y-y_0)^2 } $$

Así, podemos reescribir la ecuación de forma equivalente:

$$ \overline{OP}^2 = r^2 $$

$$ \big( \sqrt{ (x-x_0)^2 + (y-y_0)^2 } \big)^2 = r^2 $$

El resultado final es la ecuación en forma estándar de la circunferencia:

$$ (x-x_0)^2 + (y-y_0)^2 = r^2 $$

Para obtener la ecuación general, desarrollamos los cuadrados:

$$ x^2 + x_0^2 - 2xx_0 + y^2 + y_0^2 - 2yy_0 = r^2 $$

$$ x^2 + y^2 - 2x x_0 - 2y y_0 + x_0^2 + y_0^2 - r^2 = 0 $$

Si definimos a=-2x₀, b=-2y₀ y c=x₀²+y₀²-r², entonces:

$$ x^2 + y^2 - 2x_0 \cdot x - 2y_0 \cdot y + (x_0^2 + y_0^2 - r^2) = 0 $$

$$ x^2 + y^2 + a \cdot x + b \cdot y + c = 0 $$

Así obtenemos la ecuación general de la circunferencia:

$$ x^2 + y^2 + ax + by + c = 0 $$

Como a=-2x₀ y b=-2y₀, se deducen las coordenadas x₀=-a/2 y y₀=-b/2.

Por tanto, las coordenadas (x₀, y₀) del centro de la circunferencia son:

$$ (x_0 ; y_0) = \left( - \frac{a}{2} ; - \frac{b}{2} \right) $$

Para deducir la fórmula del radio, comparamos las dos ecuaciones de la circunferencia \( x^2 + x_0^2 + \frac{a}{2} x + \frac{b}{2} y + y^2 + y_0^2 - r^2 = 0 \) y \( x^2 + y^2 + ax + by + c = 0 \).

• Ecuación estándar de la circunferencia
  $$ x^2 + x_0^2 + \frac{a}{2} x + \frac{b}{2} y + y^2 + y_0^2 - r^2 = 0 $$
• Ecuación general de la circunferencia
  $$ x^2 + y^2 + ax + by + c = 0 $$

Los términos constantes en ambas ecuaciones son r², x₀² y y₀² en la primera, y c en la segunda.

Nota. Llamamos "término constante" a aquellos valores que no están multiplicados por ninguna variable, permaneciendo inalterables sin importar los valores que tomen las variables x o y en la ecuación.

Al ser constantes, estos términos deben coincidir en ambas ecuaciones.

En otras palabras, la suma de los términos constantes de la primera ecuación x₀² + y₀² - r² es igual al término "c" de la segunda ecuación de la circunferencia.

Por tanto, igualamos los términos constantes de ambas ecuaciones:

$$ x_0^2 + y_0^2 - r^2 = c $$

De este modo, se puede despejar el radio \(r\) de la circunferencia:

$$ r^2 = x_0^2 + y_0^2 - c $$

$$ \sqrt{ r^2 } = \sqrt{ x_0^2 + y_0^2 - c } $$

$$ r = \sqrt{ x_0^2 + y_0^2 - c } $$

Y, sabiendo que a=-2x₀ y b=-2y₀, también podemos escribir:

$$ r = \sqrt{ \left( - \frac{a}{2} \right)^2 + \left( - \frac{b}{2} \right)^2 - c } $$

Así obtenemos la fórmula del radio que queríamos deducir.

Estudio de casos de la ecuación de la circunferencia

La ecuación general de la circunferencia en el plano cartesiano se expresa así:

$$ x^2 + y^2 + ax + by + c = 0 $$

Aquí, los coeficientes \( a \), \( b \) y \( c \) son números reales que determinan la posición y las características de la circunferencia en el plano. A continuación se describen los principales casos particulares:

• Centro de la circunferencia en el origen
  Para trazar una circunferencia con centro en el origen del sistema de coordenadas, basta con igualar a cero los coeficientes \( a \) y \( b \): \[ x^2 + y^2 + c = 0 \]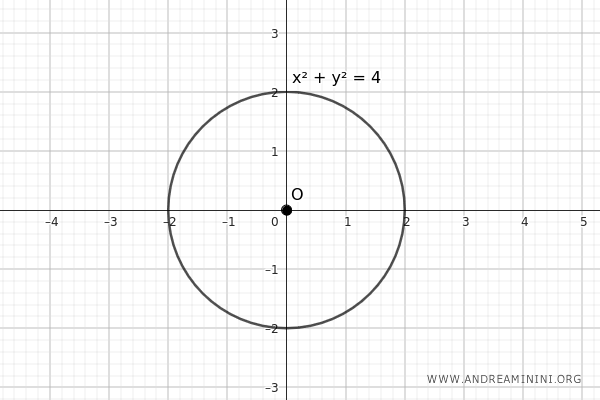
• Centro de la circunferencia sobre el eje \( x \)
  Una circunferencia cuyo centro se encuentra sobre el eje de las abscisas (eje \( x \)) tiene el coeficiente \( b \) igual a cero: \[ x^2 + y^2 + ax + c = 0 \]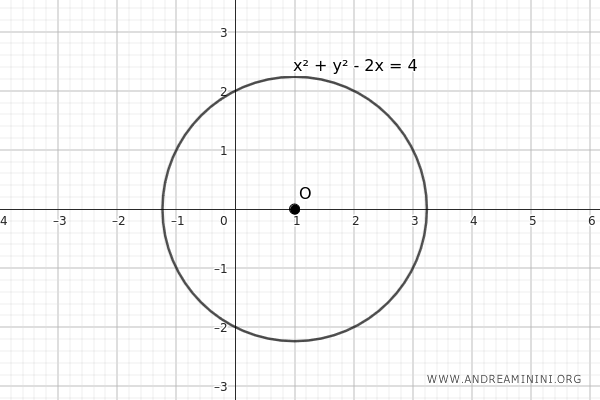
• Centro de la circunferencia sobre el eje \( y \)
  Una circunferencia cuyo centro se sitúa sobre el eje de las ordenadas (eje \( y \)) presenta el coeficiente \( a \) igual a cero: \[ x^2 + y^2 + by + c = 0 \]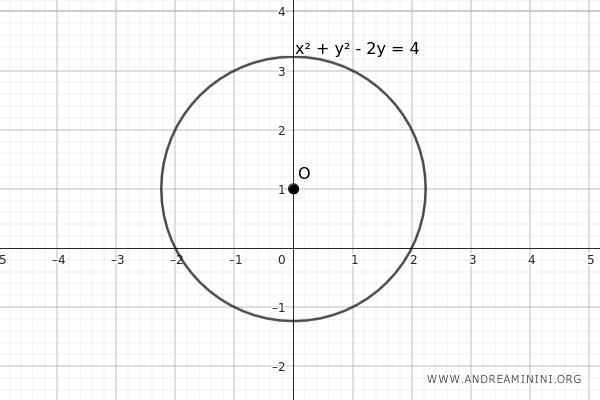
• Circunferencia que pasa por el origen
  Una circunferencia pasa por el origen de coordenadas si el coeficiente \( c \) es igual a cero: \[ x^2 + y^2 + ax + by = 0 \]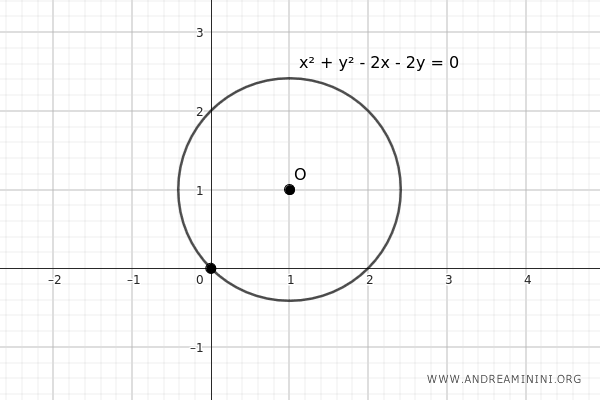

Nota. Combinando estos casos se pueden obtener otras configuraciones. Por ejemplo, si se desea una circunferencia cuyo centro esté sobre el eje \( x \) (\( b = 0 \)) y que además pase por el origen (\( c = 0 \)), basta con aplicar ambas condiciones: $$ x^2 + y^2 + ax = 0 $$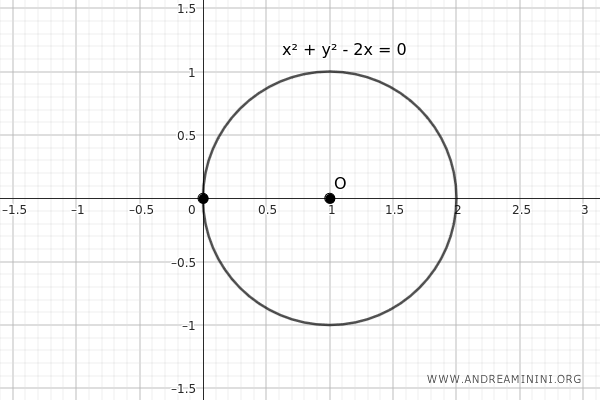

Observaciones

Algunas consideraciones y apuntes adicionales sobre la ecuación de la circunferencia:

• Cómo obtener la ecuación de la circunferencia conociendo el centro y el radio
  Dado que todos los puntos de la circunferencia se encuentran a una distancia constante - el radio - de su centro, si se conocen el centro C(x₀, y₀) y el radio r, la ecuación de la circunferencia se obtiene mediante la siguiente fórmula: $$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
• La ecuación de la circunferencia dados los extremos del diámetro
  Para hallar la ecuación de una circunferencia conocidos los extremos A y B de un diámetro, se calcula el centro como el punto medio del segmento AB: $$ C \left( \frac{x_A + x_B}{2} ; \frac{y_A + y_B}{2} \right) $$ y el radio como la mitad de la distancia entre los puntos A y B: $$ r = \frac{1}{2} \cdot \sqrt{(x_A - x_B)^2 + (y_A - y_B)^2} $$ Una vez obtenidos el centro y el radio, basta aplicar la fórmula: $$ (x - x_0)^2 + (y - y_0)^2 = r^2 $$
• La ecuación de la circunferencia que pasa por tres puntos no alineados
  Dados tres puntos no colineales A(x₁, y₁), B(x₂, y₂) y C(x₃, y₃), la ecuación de la circunferencia que pasa por ellos se obtiene resolviendo el siguiente sistema para determinar los valores de "a", "b" y "c": $$ \begin{cases} x_1^2 + y_1^2 + a x_1 + b y_1 + c = 0 \\ x_2^2 + y_2^2 + a x_2 + b y_2 + c = 0 \\ x_3^2 + y_3^2 + a x_3 + b y_3 + c = 0 \end{cases} $$ Una vez hallados los coeficientes "a", "b" y "c", se sustituyen en la ecuación general de la circunferencia: $$ x^2 + y^2 + a x + b y + c = 0 $$
  

Y así sucesivamente.