Eje Radical
El eje radical de dos circunferencias no concéntricas es el conjunto de puntos que poseen la misma potencia respecto a ambas circunferencias.
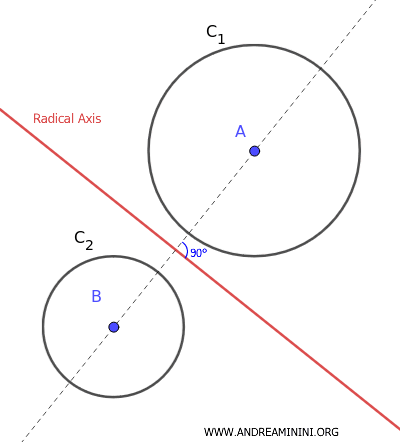
La potencia de un punto \( P \), de coordenadas \((x_0, y_0)\), respecto a una circunferencia con centro \((h, k)\) y radio \( r \), se define como el cuadrado de la distancia del punto al centro menos el cuadrado del radio.
$$ \text{Potencia} = d^2 - r^2 $$
donde \( d \) es la distancia entre el punto \( P \) y el centro de la circunferencia, y \( r \) es el radio.
La distancia entre el punto \( P \) y el centro \((h, k)\) se calcula mediante:
$$ d = \sqrt{(x_0 - h)^2 + (y_0 - k)^2} $$
Por tanto, la potencia del punto \( P \) respecto a la circunferencia en forma estándar se expresa así:
$$ \text{Potencia} = (x_0 - h)^2 + (y_0 - k)^2 - r^2 $$
El eje radical está formado por todos los puntos para los cuales la diferencia de potencias respecto a las dos circunferencias es cero:
$$ (x_0 - h_1)^2 + (y_0 - k_1)^2 - r_1^2 = (x_0 - h_2)^2 + (y_0 - k_2)^2 - r_2^2$$
Si las circunferencias están dadas en su forma general, se puede hallar el eje radical restando una ecuación de la otra: $$ x^2 - y^2 + ax + by + c = x^2 - y^2 + a'x + b'y + c' $$ $$ \require{cancel} \cancel{x^2} - \cancel{y^2} + ax + by + c = \cancel{x^2} - \cancel{y^2} + a'x + b'y + c' $$ $$ ax + by + c - a'x - b'y - c' = 0 $$ $$ (a - a')x + (b - b')y + c - c' = 0 $$ Esto da lugar a una ecuación lineal en \( x \) e \( y \), cuyas soluciones son los puntos que pertenecen al eje radical. Si despejamos \( y \), obtenemos: $$ y = - \frac{a-a'}{b-b'} x - \frac{c-c'}{b-b'} $$ Así, podemos calcular la pendiente del eje radical: $$ m = - \frac{a-a'}{b-b'} $$
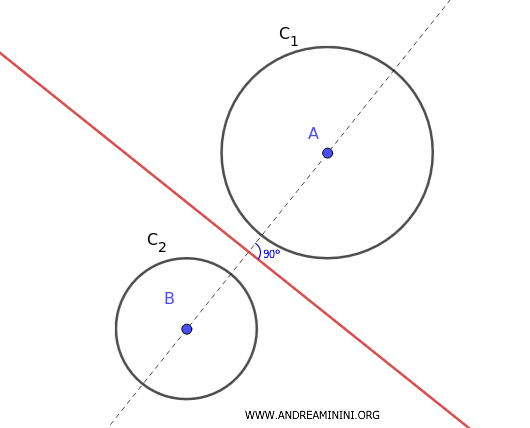
El eje radical es una recta perpendicular a la línea que une los centros de ambas circunferencias.
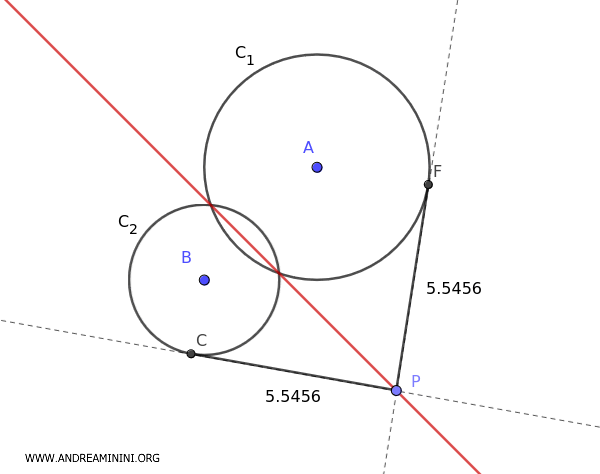
Para cualquier punto \( P \) situado sobre el eje radical, las longitudes de los segmentos tangentes trazados a ambas circunferencias son iguales. Por ejemplo, \( PC \cong PF \).
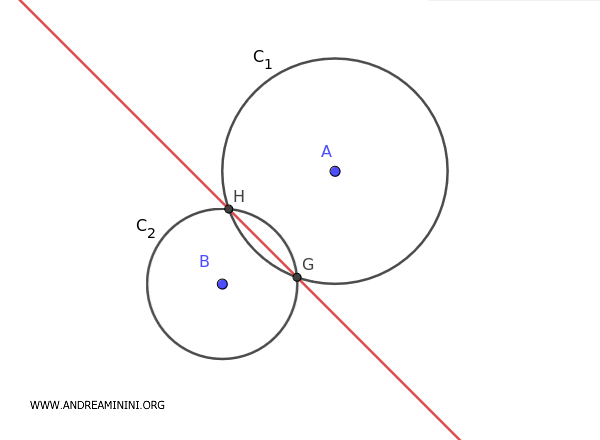
Si las dos circunferencias se cortan, el eje radical pasa por los puntos de intersección.
Si las circunferencias son tangentes entre sí, el eje radical pasa por el punto de tangencia.
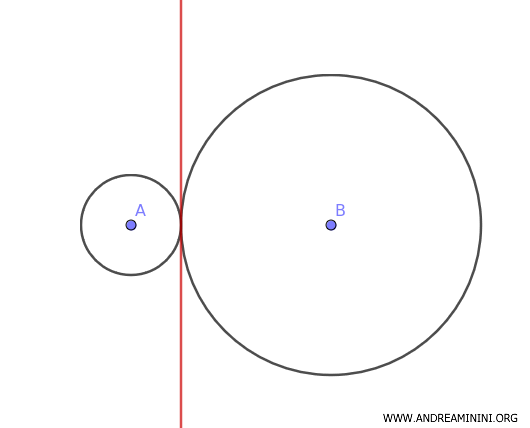
Ejemplo Práctico
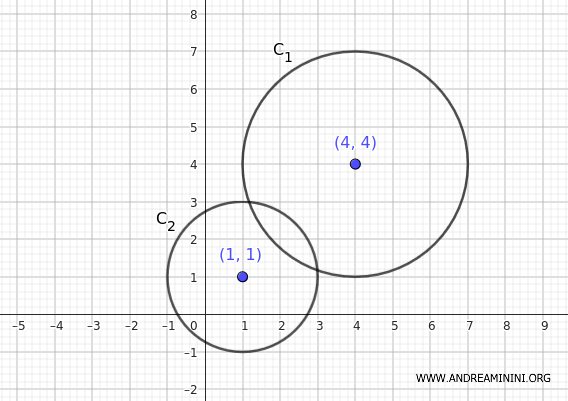
Consideremos dos circunferencias dadas en forma estándar:
$$ C_1 : \ (x - 4)^2 + (y - 4)^2 = 9 $$
$$ C_2 : \ (x - 1)^2 + (y - 1)^2 = 4 $$
La primera circunferencia tiene su centro en el punto (4, 4) y radio 3, ya que \( r^2 = 9 \), por lo que \( r = 3 \).
La segunda circunferencia tiene centro en (1, 1) y radio 2, dado que \( r^2 = 4 \), es decir, \( r = 2 \).
La potencia de un punto genérico \( P(x,y) \) respecto a la primera circunferencia, cuyo centro está en \( (h,k) = (4, 4) \) y radio \( r = 3 \), es:
$$ W_1 = (x - h)^2 + (y - k)^2 - r^2 $$
$$ W_1 = (x - 4)^2 + (y - 4)^2 - 3^2 $$
$$ W_1 = (x - 4)^2 + (y - 4)^2 - 9 $$
La potencia del mismo punto \( P(x,y) \) respecto a la segunda circunferencia, cuyo centro es \( (h,k) = (1, 1) \) y radio \( r = 2 \), es:
$$ W_2 = (x - h)^2 + (y - k)^2 - r^2 $$
$$ W_2 = (x - 1)^2 + (y - 1)^2 - 2^2 $$
$$ W_2 = (x - 1)^2 + (y - 1)^2 - 4 $$
Para determinar el eje radical, igualamos ambas potencias:
$$ W_1 = W_2 $$
$$ (x - 4)^2 + (y - 4)^2 - 9 = (x - 1)^2 + (y - 1)^2 - 4 $$
Simplificamos esta ecuación para obtener la recta que representa el eje radical:
$$ x^2 - 8x + 16 + y^2 - 8y + 16 - 9 = x^2 - 2x + 1 + y^2 - 2y + 1 - 4 $$
$$ -8x - 8y + 23 = -2x - 2y - 2 $$
$$ -8x + 2x - 8y + 2y = -2 - 23 $$
$$ -6x - 6y = -25 $$
$$ 6x + 6y = 25 $$
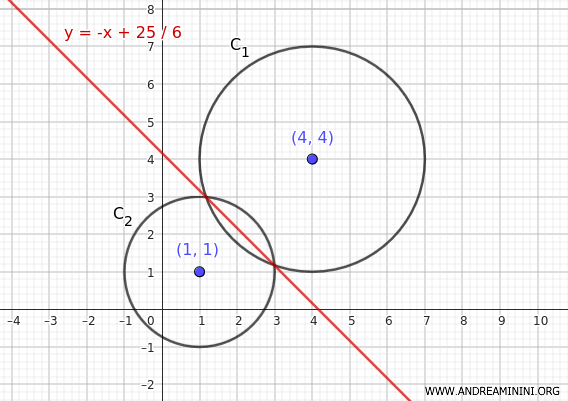
$$ y = -x + \frac{25}{6} $$
Dado que las dos circunferencias se intersectan, el eje radical es la recta que pasa por los puntos de intersección.
Ejemplo 2
Consideremos dos circunferencias dadas en forma general:
$$ C_1 : x^2 + y^2 - 8x - 8y + 23 = 0 $$
$$ C_2 : x^2 + y^2 - 2x - 2y - 2 = 0 $$
En este caso, desconocemos directamente los centros y radios, y para obtenerlos sería necesario completar cuadrados.
No obstante, si nuestro objetivo es únicamente hallar la ecuación del eje radical, basta con restar una ecuación general de la otra.
$$ C_1 = C_2 $$
$$ x^2 + y^2 - 8x - 8y + 23 = x^2 + y^2 - 2x - 2y - 2 $$
$$ \require{cancel} \cancel{x^2} + \cancel{y^2} - 8x - 8y + 23 = \cancel{x^2} + \cancel{y^2} - 2x - 2y - 2 $$
Esto nos deja una ecuación lineal:
$$ -8x + 2x - 8y + 2y = -2 - 23 $$
$$ -6x - 6y = -25 $$
$$ 6x + 6y = 25 $$
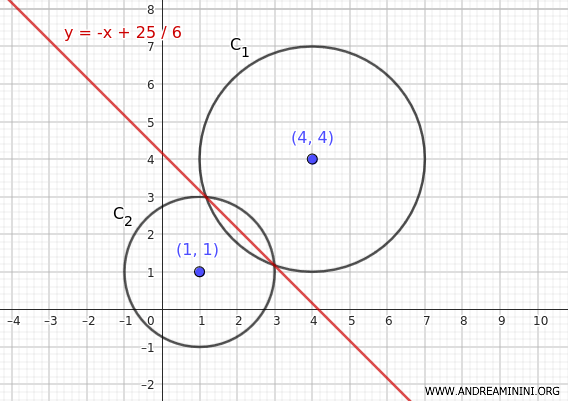
$$ y = -x + \frac{25}{6} $$
Esta es la ecuación del eje radical de ambas circunferencias.
Ejemplo 3
Consideremos dos circunferencias dadas en forma general:
$$ C_1 : x^2 + y^2 - 2x = 0 $$
$$ C_2 : x^2 + y^2 - 10x + 16 = 0 $$
Para obtener la ecuación del eje radical, restamos la primera ecuación de la segunda:
$$ x^2 + y^2 - 2x = x^2 + y^2 - 10x + 16 $$
$$ \cancel{x^2} + \cancel{y^2} - 2x = \cancel{x^2} + \cancel{y^2} - 10x + 16 $$
$$ -2x = -10x + 16 $$
$$ -2x + 10x = 16 $$
$$ 8x = 16 $$
$$ x = \frac{16}{8} $$
$$ x = 2 $$
En este caso, el eje radical es una recta paralela al eje Y que pasa por \( x = 2 \).
Como las dos circunferencias son tangentes entre sí, el eje radical pasa exactamente por el punto de tangencia.
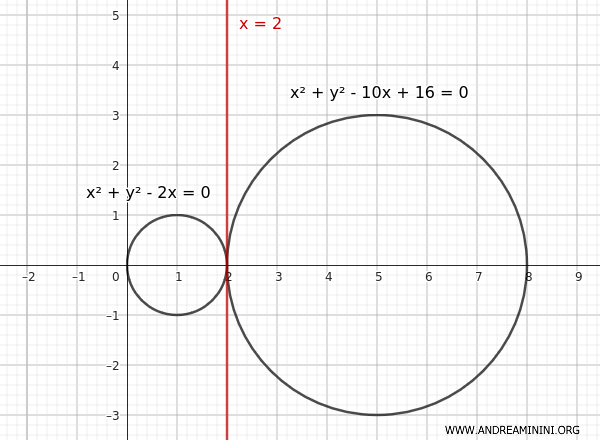
Ejemplo 4
Consideremos dos circunferencias:
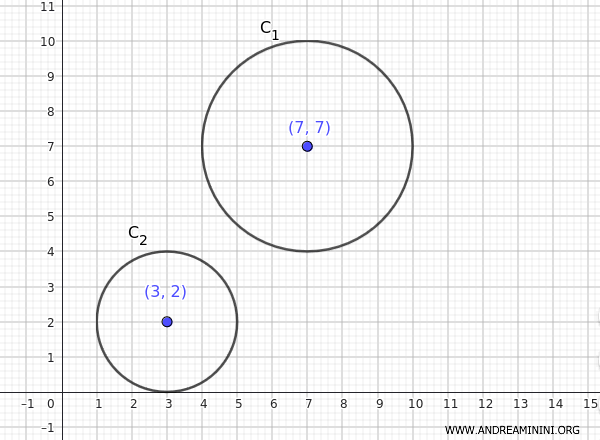
$$ C_1 : (x - 7)^2 + (y - 7)^2 = 9 $$
$$ C_2 : (x - 3)^2 + (y - 2)^2 = 4 $$
La primera circunferencia tiene centro en (h, k) = (7, 7) y radio \( r = \sqrt{9} = 3 \).
La segunda circunferencia tiene centro en (h, k) = (3, 2) y radio \( r = \sqrt{4} = 2 \).
La potencia de un punto \( P(x, y) \) respecto de la primera circunferencia, de centro (h, k) = (7, 7) y radio \( r = 3 \), se calcula así:
$$ W_1 = (x - h)^2 + (y - k)^2 - r^2 $$
$$ W_1 = (x - 7)^2 + (y - 7)^2 - 3^2 $$
$$ W_1 = (x - 7)^2 + (y - 7)^2 - 9 $$
La potencia del mismo punto \( P(x, y) \) respecto de la segunda circunferencia, de centro (h, k) = (3, 2) y radio \( r = 2 \), es:
$$ W_2 = (x - h)^2 + (y - k)^2 - r^2 $$
$$ W_2 = (x - 3)^2 + (y - 2)^2 - 2^2 $$
$$ W_2 = (x - 3)^2 + (y - 2)^2 - 4 $$
Igualamos las potencias para hallar el eje radical:
$$ W_1 = W_2 $$
$$ (x - 7)^2 + (y - 7)^2 - 9 = (x - 3)^2 + (y - 2)^2 - 4 $$
Desarrollamos los cálculos algebraicos necesarios:
$$ x^2 - 14x + 49 + y^2 - 14y + 49 - 9 = x^2 - 6x + 9 + y^2 - 4y + 4 - 4 $$
$$ \require{cancel} \cancel{x^2} - 14x + 49 + \cancel{y^2} - 14y + 49 - 9 = \cancel{x^2} - 6x + 9 + \cancel{y^2} - 4y + 4 - 4 $$
$$ -14x - 14y + 89 = -6x - 4y + 9 $$
$$ -14x + 6x - 14y + 4y = 9 - 89 $$
$$ -8x - 10y = -80 $$
$$ 10y = -8x + 80 $$
$$ y = \frac{-8x + 80}{10} $$
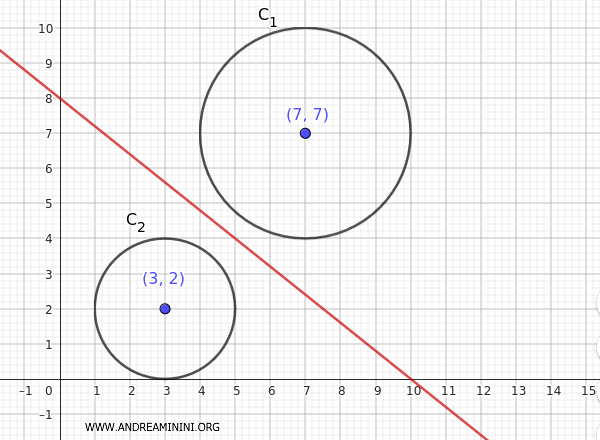
$$ y = -\frac{4x}{5} + 8 $$
Esta es la ecuación del eje radical de las dos circunferencias.
En este caso, las dos circunferencias son exteriores entre sí, por lo que el eje radical se sitúa en la región exterior a ambas.
Y así sucesivamente.