Semicircunferencia
Una semicircunferencia es la mitad de una circunferencia.
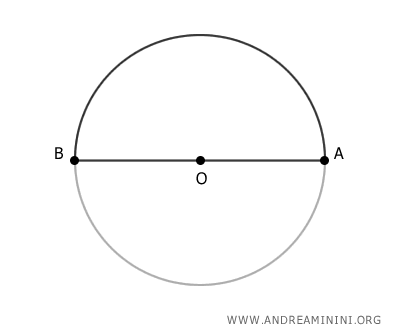
Cuando se traza un diámetro en una circunferencia, esta se divide en dos partes iguales, cada una de las cuales es una semicircunferencia.
La longitud de una semicircunferencia es la mitad de la longitud de la circunferencia completa.
$$ S_c = \pi \cdot r $$
Explicación. Si \( r \) es el radio de la circunferencia y \( C = 2\pi r \) es la longitud total de la circunferencia, la longitud de la semicircunferencia se calcula así: $$ S_c = \frac{C}{2} = \frac{2 \pi \cdot r}{2} = \pi \cdot r $$
La parte del plano comprendida entre el diámetro y la semicircunferencia se llama semicírculo.
El área de un semicírculo es la mitad del área del círculo.
$$ A_{sc} = \frac{r^2 \pi}{2} $$
Explicación. Sabiendo que el área del círculo es \( A = \pi \cdot r^2 \), el área del semicírculo se calcula de la siguiente manera: $$ A_{sc} = \frac{A}{2} = \frac{r^2 \pi}{2} $$
Observaciones
Algunas observaciones y notas sobre la semicircunferencia:
- Cualquier ángulo inscrito en una semicircunferencia es un ángulo recto.
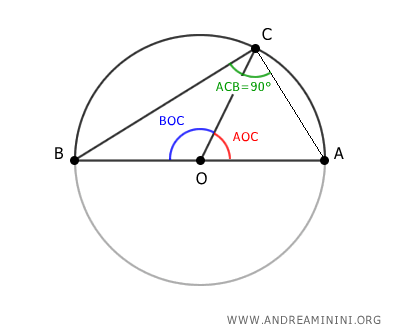
Esta propiedad se utiliza con frecuencia en geometría euclidiana.Demostración. Consideremos una circunferencia con centro en O y diámetro AB.

Tomemos un punto C cualquiera sobre la semicircunferencia delimitada por A y B. Queremos demostrar que el ángulo ACB es un ángulo recto (90°).
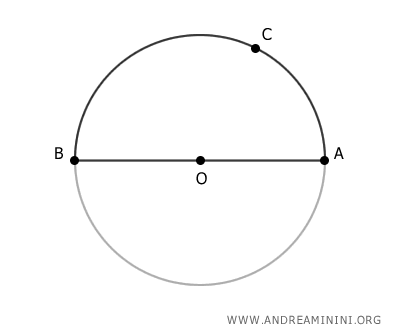
Trazamos el segmento OC.
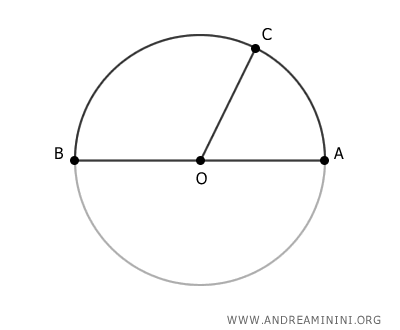
Como OA y OB son radios de la circunferencia, son congruentes \( OA \cong OB \), es decir, tienen la misma longitud. También OC es un radio, por lo que tiene la misma longitud que OA y OB. $$ \overline{OA} = \overline{OB} = \overline{OC} $$ El ángulo central AOC abarca el arco AC y el ángulo BOC abarca el arco BC. El ángulo AOB, que abarca todo el arco ACB, mide 180°, ya que corresponde a una semicircunferencia.
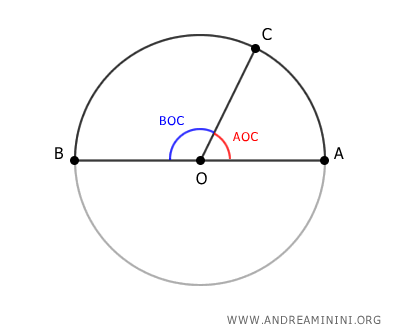
El Teorema de los Ángulos Inscritos afirma que un ángulo inscrito en una circunferencia mide la mitad del ángulo central que abarca el mismo arco. Por tanto, si el ángulo central que abarca el arco ACB es llano (AOB = 180°), entonces el ángulo inscrito ACB mide 180°/2, es decir, 90°, lo cual demuestra que ACB es un ángulo recto.
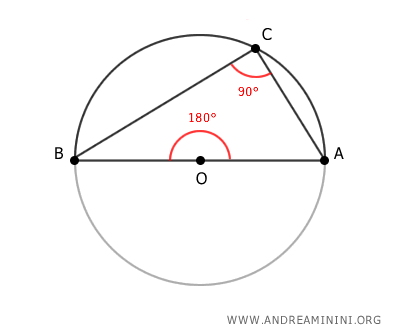
- Cualquier triángulo inscrito en una semicircunferencia es un triángulo rectángulo, cuyo diámetro es la hipotenusa.
Esto se deduce igualmente del Teorema de los Ángulos Inscritos. Si el ángulo central mide 180°, entonces el ángulo inscrito correspondiente mide exactamente la mitad, es decir, 90°.
Y así sucesivamente.