Fórmula para el centro de una circunferencia
Para determinar las coordenadas \((x, y)\) del centro de una circunferencia a partir de su ecuación general $$ x^2 + y^2 + Dx + Ey + F = 0 $$, se emplea la siguiente fórmula: $$ O(x, y) = \left( -\frac{D}{2}, -\frac{E}{2} \right) $$
Cuando la ecuación de la circunferencia se expresa en su forma ordinaria:
\[ (x - h)^2 + (y - k)^2 = r^2 \]
El centro y el radio de la circunferencia en el plano cartesiano resultan inmediatamente evidentes:
- \( (h, k) \) son las coordenadas del centro de la circunferencia.
- \( r \) es el radio de la circunferencia.
Si, en cambio, la ecuación se presenta en forma general:
\[ x^2 + y^2 + Dx + Ey + F = 0 \]
El centro \((h, k)\) puede calcularse mediante las siguientes expresiones:
$$ h = -\frac{D}{2} $$
$$ k = -\frac{E}{2} $$
En estas fórmulas, \( D \) y \( E \) representan los coeficientes de los términos en \( x \) y \( y \) de la ecuación general $ x^2 + y^2 + Dx + Ey + F = 0 $.
Por lo tanto, el centro de la circunferencia está dado por las coordenadas \((-D/2, -E/2)\).
Nota: Otra forma de encontrar las coordenadas del centro consiste en transformar la ecuación general $ x^2 + y^2 + Dx + Ey + F = 0 $ a su forma ordinaria $ (x - h)^2 + (y - k)^2 = r^2 $ completando cuadrados y ajustando los términos necesarios.
Ejemplo
Veamos un ejemplo práctico para ilustrar el procedimiento.
Consideremos la ecuación general de una circunferencia:
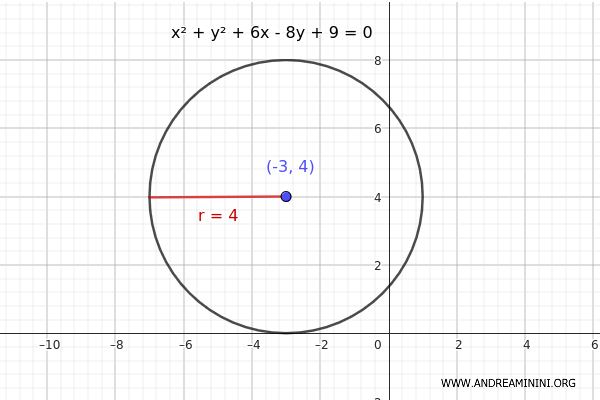
\[ x^2 + y^2 + 6x - 8y + 9 = 0 \]
Para determinar el centro de la circunferencia, identificamos los coeficientes \( D \) y \( E \). En este caso, son:
$$ D = 6 $$
$$ E = -8 $$
Aplicamos las fórmulas para calcular las coordenadas \( h \) y \( k \) del centro:
$$ h = -\frac{D}{2} = -\frac{6}{2} = -3 $$
$$ k = -\frac{E}{2} = -\frac{-8}{2} = 4 $$
Por lo tanto, el centro de la circunferencia es \((-3, 4)\).
Demostración
Para demostrar cómo se obtiene el centro de la circunferencia a partir de su ecuación general \( x^2 + y^2 + Dx + Ey + F = 0 \), es necesario transformarla a su forma ordinaria \((x - h)^2 + (y - k)^2 = r^2\).
Partimos de la ecuación general de la circunferencia:
$$ x^2 + y^2 + Dx + Ey + F = 0 $$
Agrupamos los términos que involucran \( x \) y \( y \):
$$ (x^2 + Dx) + (y^2 + Ey) + F = 0 $$
Completamos el cuadrado en los términos de \( x \), sumando y restando $ \left(\frac{D}{2}\right)^2 $:
$$ (x^2 + Dx + \left(\frac{D}{2}\right)^2) - \left(\frac{D}{2}\right)^2 + (y^2 + Ey) + F = 0 $$
$$ (x + \frac{D}{2})^2 - \left(\frac{D}{2}\right)^2 + (y^2 + Ey) + F = 0 $$
Completamos también el cuadrado en los términos de \( y \), sumando y restando $ \left(\frac{E}{2}\right)^2 $:
$$ \left(x + \frac{D}{2}\right)^2 - \left(\frac{D}{2}\right)^2 + (y^2 + Ey + \left(\frac{E}{2}\right)^2) - \left(\frac{E}{2}\right)^2 + F = 0 $$
$$ \left(x + \frac{D}{2}\right)^2 - \left(\frac{D}{2}\right)^2 + \left(y + \frac{E}{2}\right)^2 - \left(\frac{E}{2}\right)^2 + F = 0 $$
Reorganizamos términos para aislar el radio:
$$ \left(x + \frac{D}{2}\right)^2 + \left(y + \frac{E}{2}\right)^2 = \left(\frac{D}{2}\right)^2 + \left(\frac{E}{2}\right)^2 - F $$
Esto nos conduce a la forma ordinaria de la ecuación de la circunferencia \((x - h)^2 + (y - k)^2 = r^2\), donde:
$$ h = -\frac{D}{2} $$
$$ k = -\frac{E}{2} $$
Por consiguiente, el centro de la circunferencia \((h, k)\) se determina mediante:
$$ \left(-\frac{D}{2}, -\frac{E}{2}\right) $$
Y el radio \( r \) se calcula así:
$$ r = \sqrt{\left(\frac{D}{2}\right)^2 + \left(\frac{E}{2}\right)^2 - F} $$
Con esto queda demostrado cómo se obtiene tanto el centro como el radio de una circunferencia a partir de su ecuación en forma general.
Y así concluye la demostración.