Teorema de Equivalencia de Áreas entre Círculo y Triángulo

El área de un círculo es equivalente a la de un triángulo cuya base coincide con la longitud de la circunferencia del círculo y cuya altura es igual a su radio. $$ \pi \cdot r^2 = \frac{1}{2} \cdot c \cdot r $$

En términos sencillos, un círculo puede considerarse equivalente a un triángulo que tiene como base su circunferencia y como altura su radio.

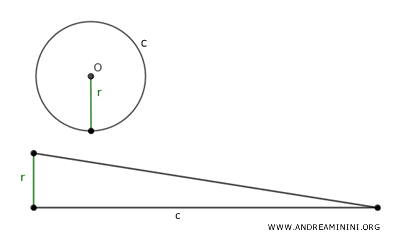
Visualización del teorema de equivalencia entre círculo y triángulo

Para calcular el área de un círculo, basta con multiplicar pi (π=3.14...) por el radio elevado al cuadrado (r).

$$ A = \pi r^2 $$

Por otra parte, la longitud de la circunferencia $ c $ se obtiene multiplicando el doble de pi por el radio (r).

$$ c = 2\pi r $$

Si consideramos un triángulo cuya base es la circunferencia del círculo ($c = 2\pi r$) y cuya altura es el radio del círculo ($h = r$), su área $A_t$ se calcula así:

$$ A_t = \frac{1}{2} \cdot \text{base} \cdot \text{altura} = \frac{1}{2} \cdot C \cdot r = \frac{1}{2} \cdot 2\pi r \cdot r = \pi r^2 $$

Por lo tanto, el círculo y dicho triángulo poseen exactamente la misma área.

Nota: Aunque este teorema no suele figurar de forma explícita en los textos clásicos de geometría, ofrece una relación fascinante entre el área de un círculo y la de un triángulo. Es más bien una observación geométrica ingeniosa que surge de manera natural a partir de las fórmulas para calcular las áreas de círculos y triángulos.

La Demostración

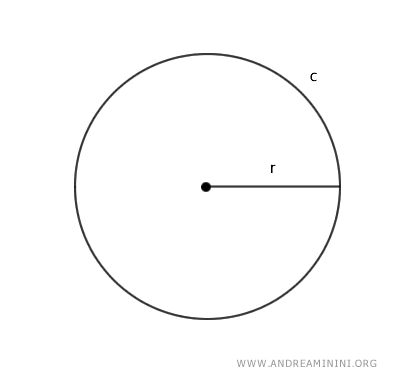
Imaginemos un círculo de circunferencia c y radio r.

Ilustración de un círculo

Construyamos en su interior un polígono regular inscrito, como un hexágono.

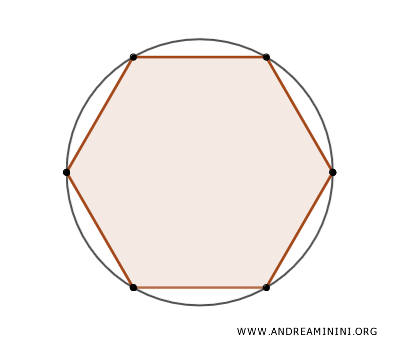
Hexágono inscrito en un círculo

Se deduce que el área del polígono inscrito $ A_p $ es menor que el área del círculo $ A_c $.

$$ A_p < A_c $$

A continuación, construyamos un polígono regular circunscrito alrededor del círculo, con el mismo número de lados.

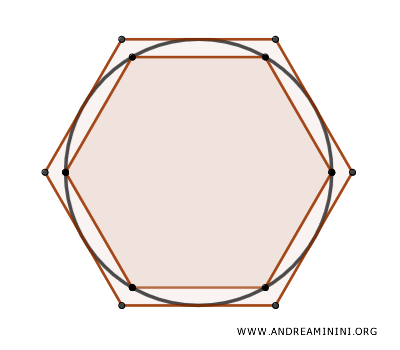
Hexágono circunscrito alrededor de un círculo

De ello se concluye que el área del polígono circunscrito $ A_{p'} $ es mayor que el área del círculo $ A_c $.

$$ A_p < A_c < A_{p'} $$

Así, el área del círculo $ A_c $ se sitúa entre las áreas de los polígonos regulares inscritos y circunscritos.

A medida que aumentamos el número de lados de estos polígonos, sus áreas $ A_p $ se aproximan cada vez más al área del círculo $ A_c $.

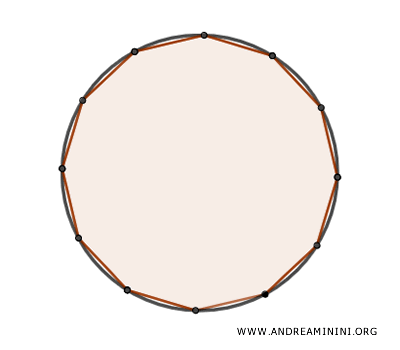
Polígono con más lados inscrito en un círculo

Si llevamos este razonamiento al límite, podemos considerar un polígono regular de infinitos lados que tendría exactamente la misma área que el círculo.

$$ A_c = A_p $$

De acuerdo con el teorema sobre polígonos circunscribibles, cualquier polígono regular es equivalente a un triángulo cuya base es igual al perímetro del polígono y cuya altura corresponde a su apotema.

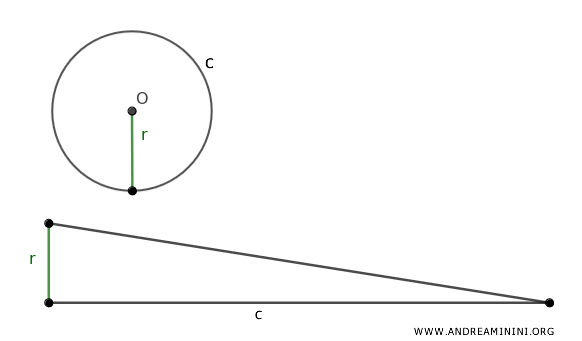
Visualización del teorema de equivalencia entre polígono regular y triángulo

Nota: En el caso de un polígono regular con infinitos lados, el apotema coincide con el radio del círculo circunscrito, de modo que la altura del triángulo es igual al radio del círculo.

Por tanto, el área del polígono de infinitos lados es igual a la del triángulo equivalente:

$$ A_c = A_p = A_t = \frac{1}{2} \cdot p \cdot a $$

Donde $ p $ es el perímetro del polígono y $ a $ es su apotema.

Dado que el perímetro del polígono equivale a la circunferencia $ p = c $ y el apotema coincide con el radio del círculo $ a = r $:

$$ A_c = A_p = A_t = \frac{1}{2} \cdot c \cdot r $$

En conclusión, el área del círculo $ A_c $ es igual a la del triángulo cuya base es la circunferencia y cuya altura es el radio.

$$ A_c = \frac{1}{2} \cdot c \cdot r $$

Comprobación Rápida: Recordando la fórmula del área del círculo $ A_c = \pi r^2 $ y comparándola con $$ A_c = \frac{1}{2} \cdot c \cdot r $$ $$ \pi r^2 = \frac{1}{2} \cdot c \cdot r $$ y teniendo en cuenta la fórmula de la circunferencia $ c = 2 \pi r $, se obtiene: $$ \pi r^2 = \frac{1}{2} \cdot ( 2 \pi r ) \cdot r $$ lo cual se simplifica a $$ \require{cancel} \pi r^2 = \pi r^2 $$ confirmando así la validez del teorema.

Y así sucesivamente.