Cálculo del Área de un Círculo
La fórmula para calcular el área de un círculo (A) es: $$ A = \pi r^2 $$ donde \(r\) es el radio del círculo y $ \pi $ es la constante pi, un valor fundamental en matemáticas.
El símbolo \(\pi\) (pi) hace referencia a la constante pi, cuyo valor aproximado es 3.14159. Para facilitar los cálculos, suele redondearse a 3.14.
Un Ejemplo Ilustrativo
Veamos el caso de un círculo cuyo radio (r) es 2.2361.
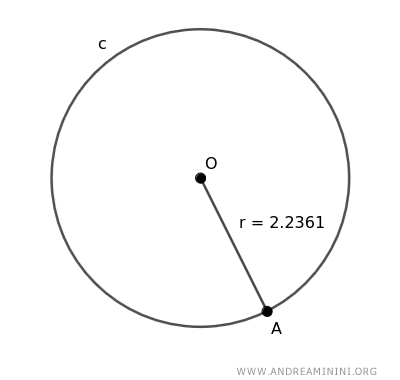
Para calcular su área, aplicamos la fórmula:
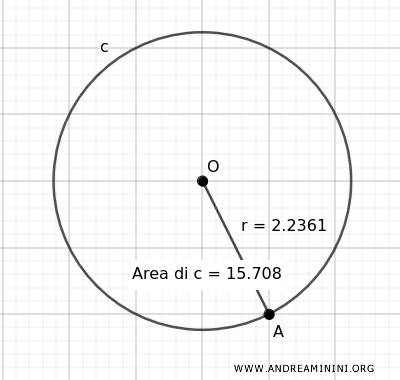
$$ A = \pi r^2 = 15.708 $$
Así, el área de este círculo es, aproximadamente, de 15.708 unidades cuadradas.
Verificación: Para confirmar el resultado, el área se calculó también utilizando GeoGebra, obteniendo el mismo valor.
Demostración
Consideremos un círculo de radio r y circunferencia c.
Está demostrado que el área de un círculo es equivalente al área de un triángulo cuya base es la circunferencia y cuya altura es el radio.
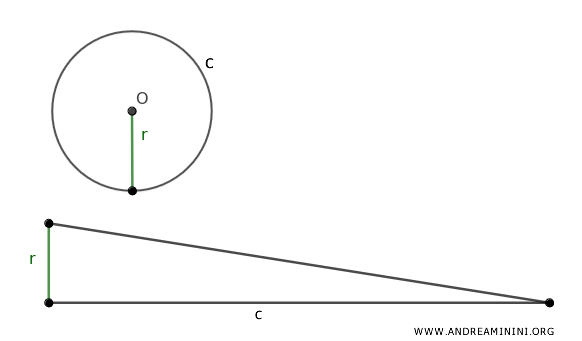
En virtud de esta equivalencia, el área del círculo coincide con la del triángulo, que se determina como la mitad del producto de la base por la altura:
$$ A_c = \frac{1}{2} \cdot \text{base} \cdot \text{altura} $$
En este caso, la base es la circunferencia (c) y la altura corresponde al radio (r).
$$ A_c = \frac{1}{2} \cdot c \cdot r $$
Sabiendo que la longitud de la circunferencia es $ c = 2 \pi r $,
$$ A_c = \frac{1}{2} \cdot (2 \pi r) \cdot r $$
$$ \require{cancel} A_c = \pi r^2 $$
Esta deducción confirma la fórmula que utilizamos para calcular el área de un círculo.
Y así sucesivamente.