Principios de Congruencia en los Círculos
Dentro de un círculo, se pueden establecer relaciones de congruencia entre:
- dos ángulos centrales
- dos arcos
- dos cuerdas
- dos segmentos circulares
- dos sectores circulares
Cuando cualquiera de estos elementos es congruente, las figuras asociadas también lo son.
En términos sencillos, todas estas figuras geométricas en el interior de un círculo están interconectadas; la congruencia de un elemento, como los ángulos centrales o las cuerdas, implica la congruencia de los demás.
Nota: Es fundamental tener presente que la congruencia entre elementos dentro de un mismo círculo - como ángulos centrales, arcos, cuerdas, sectores o segmentos circulares - no implica que dos círculos distintos sean congruentes entre sí. Para determinar si dos círculos son congruentes, la única manera es comparar sus radios.
Esto se debe a que cada una de estas figuras está estrechamente vinculada con las demás. Por ejemplo, un arco está directamente relacionado con su ángulo central, con las cuerdas que lo delimitan, con su sector circular y con su segmento circular.
Tomemos, por ejemplo, la cuerda AB en un círculo.
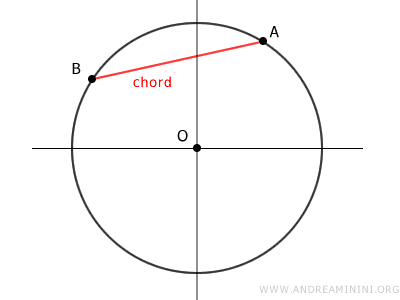
Esta cuerda AB determina un arco AB, que a su vez está asociado a un ángulo central α, a un sector circular y a un segmento circular.
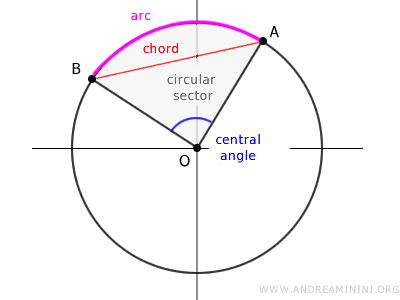
Estas relaciones son biunívocas, lo que significa que a cada arco le corresponde exactamente un único ángulo central, y viceversa.
Por lo tanto, la congruencia entre dos cuerdas en un mismo círculo asegura también la congruencia de sus respectivos arcos, sectores circulares, segmentos circulares y ángulos centrales.
Este principio se extiende de igual forma a todas las demás figuras.