Eje Central de un Haz de Circunferencias
El eje central de un haz de circunferencias es la recta que constituye el lugar geométrico de los centros de todas las circunferencias que conforman dicho haz.

En otras palabras, es la línea sobre la cual se sitúan los centros de todas las circunferencias generadas a partir de una familia determinada de circunferencias.
Un haz de circunferencias está formado por el conjunto de todas las circunferencias que pueden expresarse mediante la ecuación general:
$$ C_1 + \lambda C_2 = 0 $$
donde \(C_1\) y \(C_2\) son dos circunferencias generadoras del haz, y \(\lambda\) es un parámetro real.
El eje central de este haz es la recta que pasa por los centros de las dos circunferencias \(C_1\) y \(C_2\), y es perpendicular al eje radical.
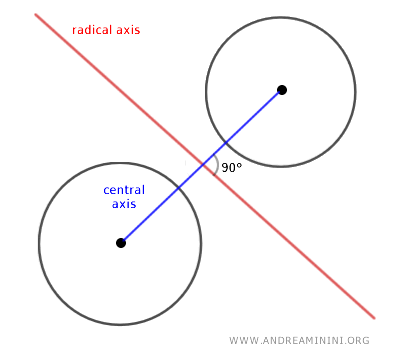
Todas las circunferencias generadas dentro del haz tienen sus centros situados sobre el eje central.
Por eso, puede considerarse como una “trayectoria de centros” para las circunferencias que forman parte del haz.

Si las circunferencias generadoras \(C_1\) y \(C_2\) son concéntricas (es decir, tienen el mismo centro), el eje central del haz se reduce a un único punto, que es el centro común de ambas circunferencias.
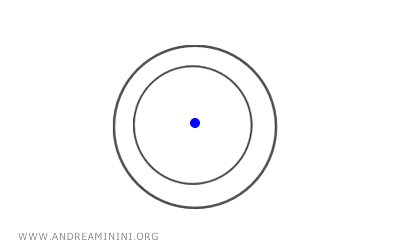
Nota: El concepto de eje central puede extenderse a dimensiones superiores. Por ejemplo, en el análisis de haces de esferas en geometría tridimensional, el eje central se convierte en un plano sobre el que se encuentran los centros de todas las esferas del haz.
Ejemplo Práctico
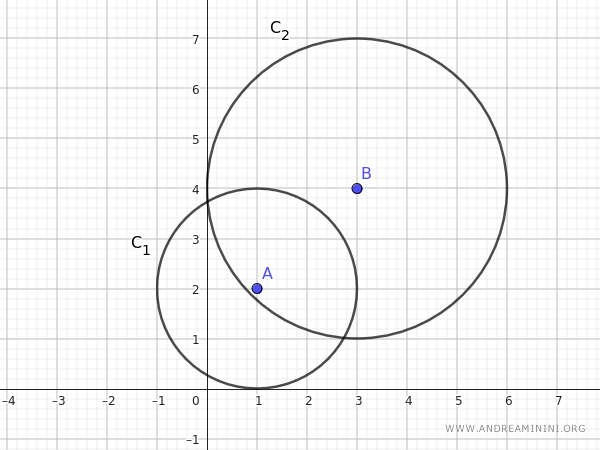
Consideremos dos circunferencias generadoras cuyas ecuaciones son:
$$ C_1: (x - 1)^2 + (y - 2)^2 - 4 = 0 $$
$$ C_2: (x - 3)^2 + (y - 4)^2 - 9 = 0 $$
Los centros de las circunferencias \(C_1\) y \(C_2\) se encuentran en los puntos \( A = (1, 2) \) y \( B = (3, 4) \), respectivamente.
El eje central del haz es la recta que pasa por estos dos puntos. Su ecuación puede obtenerse aplicando la ecuación de la recta que pasa por dos puntos:
$$ \frac{y - y_1}{y_2 - y_1} = \frac{x - x_1}{x_2 - x_1} $$
Sustituyamos las coordenadas de los centros de las circunferencias:
$$ \frac{y - 2}{4 - 2} = \frac{x - 1}{3 - 1} $$
$$ \frac{y - 2}{2} = \frac{x - 1}{2} $$
Multiplicando ambos miembros por 2, se obtiene:
$$ y - 2 = x - 1 \implies y = x + 1 $$
Por tanto, el eje central del haz formado por estas circunferencias es la recta \( y = x + 1 \).
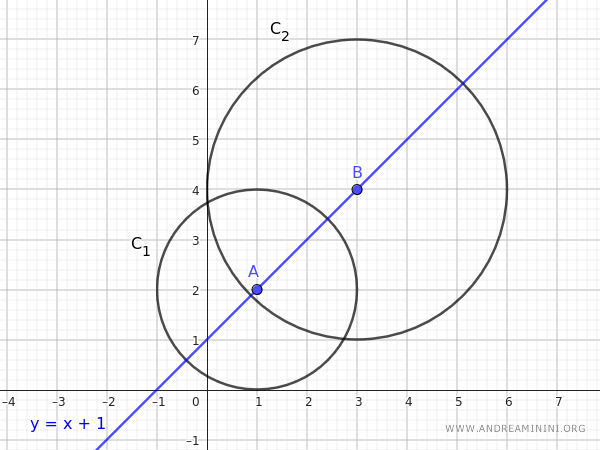
El eje central del haz de circunferencias es, en definitiva, la recta que contiene los centros de todas las circunferencias que lo integran.
Procedamos ahora a construir el haz de circunferencias a partir de las dos generadoras:
$$ C_1 + \lambda C_2 = 0 $$
$$ \big[ (x - 1)^2 + (y - 2)^2 - 4 \big] + \lambda \cdot \big[ (x - 3)^2 + (y - 4)^2 - 9 \big] = 0 $$
Generemos una circunferencia del haz eligiendo el valor \(\lambda = 2\):
$$ \big[ (x - 1)^2 + (y - 2)^2 - 4 \big] + 2 \cdot \big[ (x - 3)^2 + (y - 4)^2 - 9 \big] = 0 $$
$$ \big[ x^2 - 2x + 1 + y^2 - 4y + 4 - 4 \big] + 2 \cdot \big[ x^2 - 6x + 9 + y^2 - 8y + 16 - 9 \big] = 0 $$
$$ x^2 - 2x + 1 + y^2 - 4y + 2x^2 - 12x + 2y^2 - 16y + 32 = 0 $$
$$ 3x^2 + 3y^2 - 14x - 20y + 33 = 0 $$
Dividimos toda la ecuación entre 3:
$$ x^2 + y^2 - \frac{14}{3}x - \frac{20}{3}y + 11 = 0 $$
Esta circunferencia pertenece al haz y su centro se halla en:
$$ \left( -\frac{a}{2}, -\frac{b}{2} \right) $$
$$ \left( -\frac{-\frac{14}{3}}{2}, -\frac{-\frac{20}{3}}{2} \right) $$
$$ \left( \frac{14}{6}, \frac{20}{6} \right) $$
$$ \left( \frac{7}{3}, \frac{10}{3} \right) $$
El centro \(\left(\frac{7}{3}, \frac{10}{3}\right)\) de la circunferencia generada se encuentra sobre el eje central del haz.
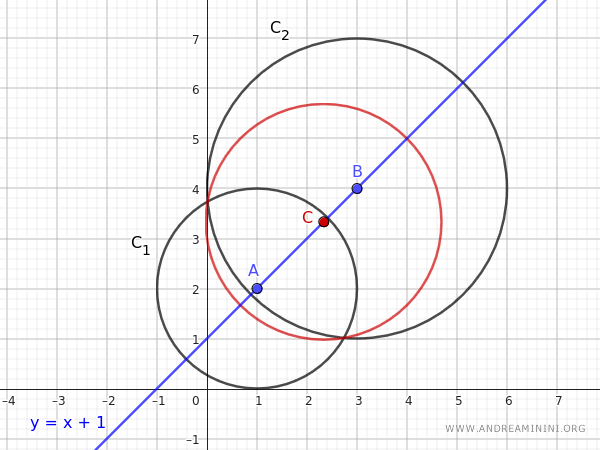
Lo mismo sucede con todas las demás circunferencias que se generan en el haz.
Y así sucesivamente.