Lugar geométrico

Un lugar geométrico es el conjunto de todos los puntos que satisfacen una determinada propiedad, regla o condición.

La propiedad que define el lugar geométrico se denomina su propiedad característica.

Para definir correctamente un lugar geométrico es necesario demostrar que todos los puntos del conjunto cumplen la misma regla, y que ningún otro punto fuera de él la satisface.

Un punto pertenece al lugar geométrico si constituye una de las soluciones de la correspondiente ecuación del lugar.

Finalidad: El concepto de lugar geométrico resulta fundamental para definir entidades geométricas, curvas y superficies a partir de propiedades que pueden expresarse mediante ecuaciones algebraicas.

Ejemplo práctico

Desde un punto de vista geométrico, una recta es el conjunto de puntos que se encuentran alineados.

Por tanto, la propiedad característica de una recta es la alineación de los puntos en el plano.

Para determinar los puntos que pertenecen a una recta, basta con encontrar los valores de x e y que satisfacen su ecuación general:

$$ ax + by + c = 0 $$

En este caso, la ecuación general de la recta es precisamente la ecuación del lugar.

Ejemplo 2

La mediatriz de un segmento es el conjunto de puntos que se encuentran a igual distancia de los extremos A y B del segmento.

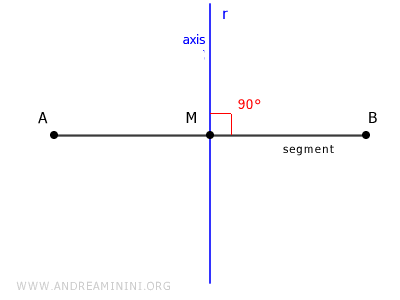
En este caso, la propiedad característica es la equidistancia respecto a los extremos del segmento, es decir: $ \overline{PA} \cong \overline{PB} $. Esto implica que la mediatriz pasa por el punto medio del segmento y es perpendicular (90°) a este.

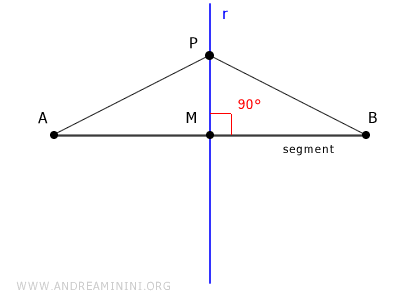
Por tanto, la ecuación del lugar expresa la igualdad de las distancias de un punto genérico P(x, y) a los extremos A(x₁, y₁) y B(x₂, y₂) del segmento:

$ \underbrace{ \sqrt{(y-y_1)^2 + (x-x_1)^2} }_{AP} = \underbrace{ \sqrt{(y-y_2)^2 + (x-x_2)^2} }_{BP} $

Esta ecuación determina todos los puntos que son equidistantes de A y B, es decir, los que pertenecen a la mediatriz del segmento AB.

Explicación: En esta ecuación se calcula la distancia de AP y BP aplicando el teorema de Pitágoras en los triángulos AMP y BMP: $$ \overline{AP} = \overline{BP} $$ $$ \underbrace{ \sqrt{ \overline{MP}^2 + \overline{AM}^2 } }_{AP} = \underbrace{ \sqrt{ \overline{MP}^2 + \overline{BM}^2 } }_{BP} $$

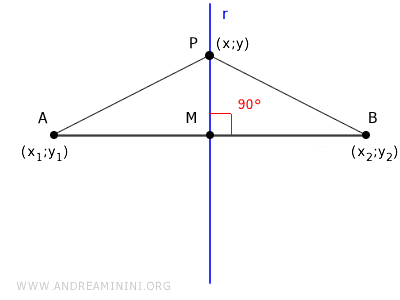
Sabiendo que MP = |y - y₁| = |y - y₂|, AM = |x - x₁| y BM = |x - x₂|, se obtiene la ecuación que expresa la equidistancia de los puntos respecto a los extremos del segmento: $$ \underbrace{ \sqrt{(y-y_1)^2 + (x-x_1)^2} }_{AP} = \underbrace{ \sqrt{(y-y_2)^2 + (x-x_2)^2} }_{BP} $$

Otros ejemplos de lugares geométricos

• La circunferencia es el lugar geométrico de los puntos de un plano que se encuentran a una distancia fija de un punto denominado "centro".
• La bisectriz de un ángulo es el lugar geométrico de los puntos equidistantes de los lados del ángulo.
• La parábola es el lugar geométrico de los puntos del plano que equidistan de un punto fijo (el foco) y de una recta fija (la directriz).
• La elipse es el lugar geométrico de los puntos cuya suma de distancias a dos puntos fijos (los focos) es constante.
• La hipérbola es el lugar geométrico de los puntos cuya diferencia de distancias a dos puntos fijos (los focos) es constante.

Y así sucesivamente.