Las magnitudes geométricas
Una clase de magnitudes geométricas es un conjunto de entes geométricos que cumplen las siguientes propiedades:
- Elementos comparables
Cada elemento de la clase puede compararse con cualquier otro de la misma clase. - La suma es una operación interna y cumple las propiedades conmutativa y asociativa
La suma de dos elementos A y B pertenecientes a la clase cumple:- la propiedad conmutativa $$ A+B = B+A $$
- la propiedad asociativa $$ A+(B+C) = (A+B)+C $$
- Existencia de una magnitud nula
Existe un elemento neutro para la suma que, al añadirse a cualquier elemento de la clase, deja el mismo elemento sin cambios.
Las clases de magnitudes geométricas constituyen un concepto fundamental en matemáticas y geometría.
Incluyen diversas medidas y propiedades de figuras y cuerpos, como la longitud, el área, el volumen, los ángulos y otras.
Ejemplos de clases de magnitudes geométricas
Entre las magnitudes geométricas más habituales podemos destacar:
- Longitud
Es la medida de una línea recta entre dos puntos. Es la dimensión más básica y se expresa en unidades como metros, centímetros, pulgadas, etc. - Área
Es la medida de la superficie bidimensional (plana) contenida en una figura, por ejemplo, la de un cuadrado o un círculo. Se mide en unidades cuadradas como metros cuadrados, centímetros cuadrados, etc. - Volumen
Mide el espacio tridimensional que ocupa un cuerpo, como una esfera o un cubo. Se expresa en unidades cúbicas como metros cúbicos, centímetros cúbicos, etc. - Ángulos
Representan la abertura o desviación entre dos líneas que se cortan en un punto común llamado “vértice”. Se miden en grados o radianes. - Superficie
Es una categoría más general que comprende tanto el área de figuras planas (bidimensionales) como el área total que recubre un objeto tridimensional.
Estas magnitudes son esenciales para el estudio y comprensión de las propiedades de las formas geométricas, tanto en matemáticas puras como en sus aplicaciones prácticas.
Magnitudes geométricas homogéneas
Dos magnitudes se consideran homogéneas cuando pertenecen a la misma clase geométrica.
En otras palabras, dos magnitudes son homogéneas si pueden compararse o combinarse directamente por tener la misma naturaleza o dimensión.
Por ejemplo, dos longitudes son homogéneas si se expresan en la misma unidad (metros, kilómetros, pulgadas, etc.), lo que permite sumarlas o restarlas.
5 metros y 3 metros son magnitudes homogéneas.
Igualmente, las áreas son homogéneas si se miden en la misma unidad (metros cuadrados, hectáreas, acres, etc.).
Dos volúmenes son homogéneos si están expresados en la misma unidad de medida (litros, metros cúbicos, etc.).
Los ángulos son homogéneos cuando se miden en la misma unidad, ya sea en grados o en radianes.
No es posible combinar directamente magnitudes no homogéneas. Por ejemplo, no tiene sentido sumar una longitud y un área, o un volumen y un ángulo, ya que pertenecen a clases distintas. No obstante, en muchos casos es posible convertir las magnitudes a unidades compatibles para hacerlas homogéneas.
Múltiplos y submúltiplos de una magnitud
Una magnitud A es un múltiplo de una magnitud homogénea B si equivale a n veces la magnitud B: $$ A = n \cdot B $$ donde n es un número natural mayor o igual que cero (n≥0).
Cuando hablamos de un múltiplo de A según un número natural n, consideramos una magnitud B que es homogénea con A. Esto significa que A y B son del mismo tipo o naturaleza (por ejemplo, ambas pueden ser longitudes, tiempos, masas, etc.).
La definición de A en función de B y n es la siguiente:
- Si n es mayor o igual que 1
A es la suma de n magnitudes iguales a B.Por ejemplo, consideremos dos segmentos AB y CD. Son magnitudes homogéneas porque ambas son longitudes. Si el segmento CD es tres veces (n=3) más largo que AB y AB mide 2 metros, entonces CD mide 6 metros y es un múltiplo de AB con n=3. $$ \overline{CD} = 3 \cdot \overline{AB} $$
- Si n es igual a 1
En este caso A es igual a B. Es evidente, ya que sumar una magnitud consigo misma una sola vez no altera su valor. $$ A=B $$ - Si n es igual a 0
A es la magnitud nula, es decir, cero. En términos prácticos, multiplicar una magnitud por cero da como resultado una magnitud nula. $$ A= 0 \cdot B = 0 $$
La definición de submúltiplo se obtiene invirtiendo la relación de múltiplo.
Si A es un múltiplo de B, entonces B es un submúltiplo de A: $$ B = \frac{1}{n} \cdot A $$ donde n es un número natural mayor que cero (n>0).
En otras palabras, B representa una fracción o parte de A.
En este caso se excluye n=0, ya que se produciría una división por cero, una operación matemáticamente imposible.
Por ejemplo, si CD es un múltiplo de AB con n=3, entonces AB es un submúltiplo de CD correspondiente a la fracción 1/3. $$ \overline{AB} = \frac{1}{3} \cdot \overline{CD} $$
Observaciones
Algunas consideraciones y notas sobre las clases de magnitudes geométricas:
- ¿Son las clases geométricas grupos?
No, las clases geométricas no forman grupos en el sentido algebraico, ya que no están definidas mediante una operación que cumpla las propiedades de los grupos.Las clases geométricas organizan y clasifican formas y figuras según propiedades comunes, mientras que los grupos son estructuras algebraicas con reglas precisas para combinar los elementos de un conjunto.
- Postulado de Eudoxo-Arquímedes
Este postulado establece que, si una magnitud es menor que otra, siempre es posible sumar un número suficiente de copias de la primera para superar a la segunda.
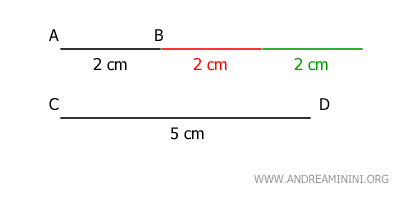
Nota. Ambas magnitudes deben ser distintas de cero. Si la menor fuera nula, todos sus múltiplos también lo serían y no podría superar a la mayor.
- Magnitudes geométricas conmensurables e inconmensurables
Dos magnitudes geométricas homogéneas son conmensurables si existe un número racional m/n que las relacione; si no existe, son inconmensurables.Ejemplo. Las longitudes de los segmentos AB y CD son conmensurables
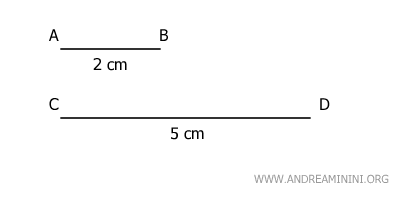
porque existe un número racional m/n que las relaciona: $$ \overline{AB} = \frac{2}{5} \cdot \overline{CD} $$ donde m y n son enteros.
Y así sucesivamente.