Magnitudes proporcionales

Dos pares de magnitudes homogéneas, A, B y C, D, donde B y D son distintas de cero, se denominan magnitudes proporcionales cuando las razones A/B y C/D son iguales. Esto puede expresarse como $$ \frac{A}{B} = \frac{C}{D} $$ o bien $$ A:B = C:D $$

En otras palabras, A guarda con B la misma relación que C con D. Dicho de forma sencilla, una proporción indica que la razón de A a B es exactamente la misma que la de C a D.

$$ \frac{A}{B} = \frac{C}{D} $$

Se lee como: «A es a B como C es a D».

Una proporción es una relación de equivalencia que solo tiene sentido cuando B y D son distintos de cero, ya que la división por cero no está definida en matemáticas.

Al igual que en las proporciones numéricas, en una proporción entre magnitudes, A y D se llaman extremos, mientras que B y C reciben el nombre de medios.

Los numeradores de las razones (A y C) se denominan antecedentes, y los denominadores (B y D) consecuentes.

Nota: No es necesario que todas las magnitudes sean homogéneas; basta con que los antecedentes lo sean entre sí y que los consecuentes también lo sean entre sí. Por ello, es posible establecer proporciones entre magnitudes no homogéneas.

El concepto de proporción entre magnitudes es fundamental en matemáticas, geometría y física, ya que permite abordar y resolver una gran variedad de problemas.

Ejemplo práctico

Supongamos que un coche azul recorre 100 km en 2 horas, mientras que un coche rojo recorre una distancia desconocida \( D \) en 4 horas.

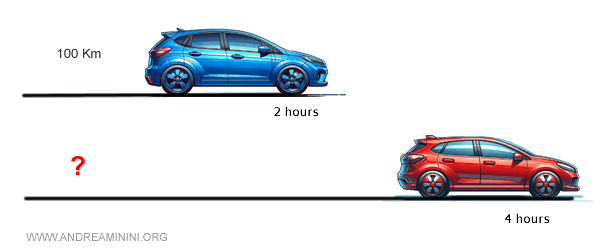
Queremos averiguar la distancia \( D \) recorrida por el coche rojo, suponiendo que ambos mantuvieron la misma velocidad constante.

Las magnitudes que comparamos son la distancia recorrida y el tiempo empleado. La proporción se plantea así:

\[ \frac{\text{Distancia}_1}{\text{Tiempo}_1} = \frac{\text{Distancia}_2}{\text{Tiempo}_2} \]

En este caso, conocemos la distancia y el tiempo del coche azul, pero del coche rojo solo conocemos el tiempo.

\[ \frac{100\, \text{km}}{2\, \text{h}} = \frac{D\, \text{km}}{4\, \text{h}} \]

Para hallar \( D \), resolvemos la proporción:

\[ \frac{100}{2} = \frac{D}{4} \]

\[ 50 = \frac{D}{4} \]

\[ D = 50 \times 4 \]

\[ D = 200\, \text{km} \]

Por lo tanto, el coche rojo recorrió 200 km en 4 horas, manteniendo la misma velocidad que el coche azul.

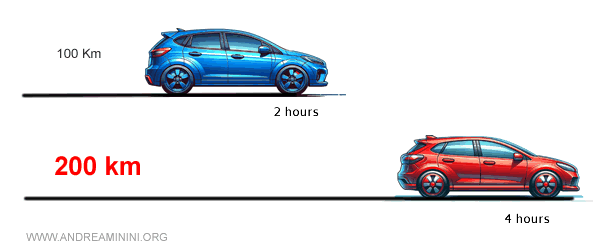
La solución es:

\[ \frac{100\, \text{km}}{2\, \text{h}} = \frac{200\,  \text{km}}{4\, \text{h}} \]

Los dos pares de magnitudes son proporcionales porque la razón es la misma:

$$ 50 \ \text{km/h} = 50 \ \text{km/h} $$

Ambos vehículos circulan a 50 kilómetros por hora.

Nota: Este ejemplo muestra cómo las proporciones permiten resolver problemas reales, especialmente cuando los antecedentes y consecuentes son magnitudes homogéneas (en este caso, distancia y tiempo) y existe una relación constante - en este ejemplo, la velocidad - entre ellas.

Propiedades de las proporciones entre magnitudes

Las propiedades de las proporciones recogen principios matemáticos que describen la relación constante entre dos o más magnitudes. Entre las más destacadas se encuentran:

• Propiedad fundamental
  En una proporción, el producto de los medios es igual al producto de los extremos.

  $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow ad = bc $$

• Propiedad de inversión
  Se pueden invertir los términos de la proporción.

  $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow \frac{b}{a} = \frac{d}{c} $$

• Propiedad de alternancia
  Es posible intercambiar los medios o los extremos.

  $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow \frac{a}{c} = \frac{b}{d} $$

• Propiedad de composición
  La suma de cada antecedente con su consecuente mantiene la proporción.

  $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow \frac{a+b}{b} = \frac{c+d}{d} $$

• Propiedad de descomposición
  Es la propiedad inversa de la composición.

  $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow \frac{a-b}{b} = \frac{c-d}{d} $$

• Propiedad de adición y sustracción
  La proporción se conserva si se suma o resta el mismo número \( n \) a los antecedentes y consecuentes, siempre que no se obtenga un denominador nulo.

  $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow\frac{a+n}{b+n} = \frac{c+n}{d+n} $$ $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow \frac{a-n}{b-n} = \frac{c-n}{d-n} $$

• Propiedad de multiplicación
  La proporción no varía si se multiplican antecedente y consecuente por un mismo número real no nulo.
  

  $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow \frac{a \cdot h}{b \cdot h} = \frac{c}{d} \ \ \ si \ \ \ h \ne 0 $$ $$ \frac{a}{b} = \frac{c}{d} \Longleftrightarrow \frac{a}{b} = \frac{c \cdot k}{d \cdot k} \ \ \ si \ \ \ k \ne 0 $$

• Propiedad de cadena de razones iguales
  Si tres pares de magnitudes homogéneas guardan la misma proporción, la razón entre la suma de los antecedentes y la suma de los consecuentes es igual a cualquiera de las proporciones iniciales.

  $$ \frac{a}{b} = \frac{c}{d} = \frac{e}{f}  \Longleftrightarrow \frac{a+c+e}{b+d+f}  = \frac{a}{b} $$

Estas propiedades son esenciales para resolver problemas con proporciones en múltiples ámbitos.

Observaciones adicionales

Algunas notas y consideraciones finales sobre las magnitudes proporcionales:

• Corolario
  Si dos pares de magnitudes homogéneas A, B y C, D son proporcionales, también lo son sus medidas: $$ \frac{A}{B} = \frac{C}{D} \Longleftrightarrow \frac{M(A)}{M(B)} = \frac{M(C)}{M(D)}  $$

  Demostración: A partir del teorema de la razón entre magnitudes homogéneas, sabemos que la razón A/B es igual a la razón entre sus medidas M(A)/M(B). Por lo tanto, si dos razones de magnitudes homogéneas son iguales $ \frac{A}{B} = \frac{C}{D} $, las razones entre sus medidas respectivas también deben ser iguales $ \frac{M(A)}{M(B)} = \frac{M(C)}{M(D)} $

• Proporciones continuas
  Una proporción entre magnitudes homogéneas es continua si los dos medios son iguales: $$ A:X = X:D $$ donde X es la media proporcional.
• Teorema del cuarto proporcional
  Dadas tres magnitudes homogéneas no nulas A, B y C, existe una única magnitud D tal que A:B = C:D $$ \frac{A}{B} = \frac{C}{D} $$

  Nota: El cuarto proporcional se obtiene a partir de A, B y C mediante la fórmula: $$ D = C \cdot \frac{B}{A} $$