Magnitudes Contiguas
Se dice que dos conjuntos de magnitudes, A y B, son magnitudes contiguas cuando se cumplen las siguientes condiciones:
- Toda magnitud del conjunto A es menor que cualquier magnitud del conjunto B.
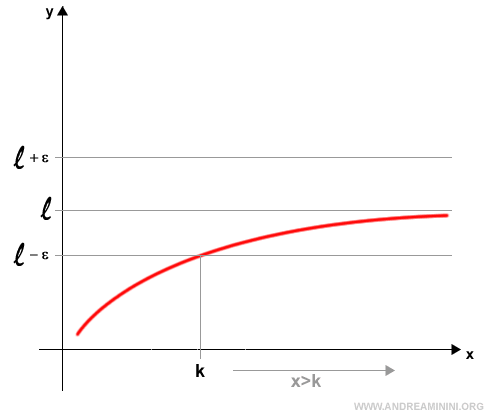
- Por muy pequeña que sea la magnitud homogénea ε que se elija, siempre es posible encontrar una magnitud de A y otra de B cuya diferencia sea inferior a ε. $$ B-A < \epsilon $$
Dicho de otro modo, existe un valor denominado elemento separador entre los dos conjuntos contiguos, que no es menor que ninguna magnitud de A ni mayor que ninguna magnitud de B.
En esencia, este elemento separador puede interpretarse como una frontera o límite preciso que separa ambos conjuntos de magnitudes.
Nota: La noción de magnitudes contiguas y de elemento separador desempeña un papel esencial en el cálculo de límites, el cálculo infinitesimal y el análisis matemático.
Por ejemplo, al definir el límite de una función en un punto, se trabaja implícitamente con magnitudes contiguas: los valores de la función pueden aproximarse tanto como se desee a un valor límite (el elemento separador) sin llegar a coincidir exactamente con él.
Esta concepción de las magnitudes matemáticas está estrechamente vinculada al postulado de continuidad, a la teoría de conjuntos y a la obra de Cantor.
Proporciona un marco conceptual sólido para abordar el infinito y la continuidad en matemáticas, y permite tratar con rigor formal nociones como la convergencia y la continuidad.
Y así sucesivamente.