Magnitudes Conmensurables e Inconmensurables

Las magnitudes conmensurables son magnitudes homogéneas que pueden compararse o medirse directamente entre sí gracias a un submúltiplo común.

Dicho de otro modo, dos magnitudes son conmensurables si pueden expresarse como múltiplos de una misma unidad de medida.

Por el contrario, si esto no es posible, dichas magnitudes se consideran inconmensurables.

Por ejemplo, pensemos en la longitud y la anchura de una habitación. Si ambas se miden en metros, pueden compararse directamente, ya que se expresan en la misma unidad de medida. En este caso, la longitud y la anchura son conmensurables.

Si dos magnitudes homogéneas, A y B, son conmensurables, pueden expresarse usando la misma unidad de medida (U):

$$ A = m \cdot U $$

$$ B = n \cdot U $$

Esto implica que pueden relacionarse entre sí, de modo que existe un número racional m/n que las vincula:

$$ A = \frac{m}{n} \cdot B $$

De forma análoga, existe un número n/m que las relaciona en sentido inverso:

$$ B = \frac{n}{m} \cdot A $$

Aquí, m y n son números enteros.

Por lo tanto, las razones m/n y n/m son números racionales.

Demostración: Consideremos la magnitud A, $$ A = m \cdot U $$. Como la unidad de medida puede expresarse en función de A y B, $$ U = \frac{1}{m} \cdot A = \frac{1}{n} \cdot B $$, sustituyendo U = (1/n) · B obtenemos que A y B se relacionan mediante la razón m/n: $$ A = m \cdot U = m \cdot ( \frac{1}{n} \cdot B ) = \frac{m}{n} \cdot B $$. De forma equivalente, pueden relacionarse mediante la razón n/m: $$ B = n \cdot U = n \cdot ( \frac{1}{m} \cdot A ) = \frac{n}{m} \cdot A $$

En resumen, las magnitudes conmensurables son aquellas que pueden medirse mutuamente mediante una razón expresada por un número racional.

Por ejemplo:

$$ A = \frac{m}{n} \cdot B $$

En otras palabras, dos magnitudes son conmensurables si la razón entre ellas es un número m/n que puede expresarse como el cociente de dos enteros.

Nota: Este concepto se remonta a la Grecia clásica, en particular a los pitagóricos, quienes descubrieron que no todas las razones entre longitudes, áreas o volúmenes podían expresarse mediante números racionales. Este hallazgo condujo al descubrimiento de los números irracionales.

Un Ejemplo Práctico

Consideremos dos segmentos, AB y CD, con longitudes de 2 y 5 centímetros, respectivamente.

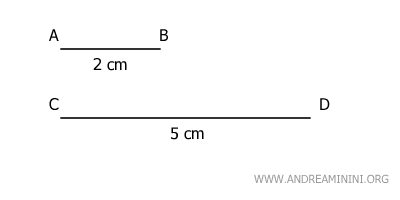
Son magnitudes homogéneas porque se pueden comparar y están expresadas en la misma unidad de medida.

Podemos pensar en el segmento AB como un múltiplo de un centímetro, concretamente dos veces (n=2):

$$ \overline{AB} = 2 \cdot ( 1 \ cm ) $$

De forma similar, el segmento CD puede considerarse un múltiplo de un centímetro, pero cinco veces (m=5):

$$ \overline{CD} = 5 \cdot ( 1 \ cm ) $$

Por lo tanto, las longitudes de AB y CD son conmensurables porque comparten un mismo submúltiplo.

En otras palabras, tanto AB como CD son múltiplos de 1 cm.

$$ 1 \ cm = \frac{1}{2} \cdot \overline{AB} $$

$$ 1 \ cm = \frac{1}{5} \cdot \overline{CD} $$

Aquí, 1 cm es la unidad de medida (U), o más precisamente, el número 1 representa el valor de dicha unidad.

$$ U = 1 \ cm = \frac{1}{2} \cdot \overline{AB} = \frac{1}{5} \cdot \overline{CD} $$

Esto significa que una magnitud puede expresarse en función de la otra.

Si la unidad de medida es U = 1 cm, el segmento AB será:

$$ \overline{AB} = 2 \cdot U $$

Y como U = (1/5) · CD:

$$ \overline{AB} = 2 \cdot ( \frac{1}{5} \cdot \overline{CD} ) $$

$$ \overline{AB} = \frac{2}{5} \cdot \overline{CD} $$

Así, AB mide 2/5 de CD.

Nota: De igual modo, podemos demostrar que CD mide 5/2 de AB: $$ \overline{CD} = \frac{5}{2} \cdot \overline{AB} $$

Ejemplo 2

Aunque dos magnitudes homogéneas se expresen en la misma unidad de medida, no necesariamente son conmensurables.

Por ejemplo, la longitud de la diagonal y la del lado de un cuadrado comparten la misma unidad (por ejemplo, metros). ¿Son conmensurables o inconmensurables?

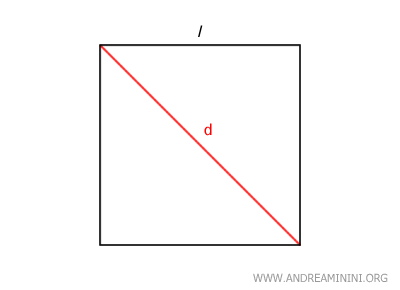
A pesar de usar la misma unidad de medida, no existe un número racional m/n que las relacione.

De la geometría básica sabemos que la diagonal (d) de un cuadrado es igual al lado (l) multiplicado por la raíz cuadrada de 2:

$$ d = l \cdot \sqrt{2} $$

Sin embargo, la raíz cuadrada de 2 es un número irracional, lo que significa que no puede expresarse como el cociente de dos enteros.

Por lo tanto, en este caso podemos afirmar que la diagonal y el lado del cuadrado son magnitudes inconmensurables cuando se utilizan números racionales.

Observaciones

Algunas consideraciones sobre la conmensurabilidad de las magnitudes:

• Dos magnitudes homogéneas inconmensurables pueden compararse usando números reales
  El hecho de que dos magnitudes homogéneas sean inconmensurables no significa que no puedan medirse o compararse. Sin embargo, en lugar de compararse mediante un número racional m/n, se relacionan mediante un número real (o irracional) α respecto a la misma unidad de medida: $$ A = \alpha \cdot B \ \ \ \ \alpha \in $$

  Ejemplo: La diagonal (d) de un cuadrado tiene una longitud igual al producto del lado por el número irracional √2: $$ d = l \cdot \sqrt{2}$$

• Conmensurabilidad en la física y las matemáticas modernas
  En física y matemáticas contemporáneas, la conmensurabilidad de dos magnitudes no se define únicamente por si su razón es racional o irracional, sino por la posibilidad de medirlas mutuamente con una medida común. En este sentido, la conmensurabilidad alude a la capacidad de describir distintas magnitudes físicas en términos de unidades compartidas o relaciones matemáticas, lo que facilita su comparación e integración en teorías unificadas como la relatividad o la mecánica cuántica.
• Conmensurabilidad en física teórica
  En contextos más avanzados que la geometría elemental, como la física teórica, el concepto de conmensurabilidad puede adquirir matices adicionales.

  Por ejemplo, en la teoría de la relatividad de Einstein, conceptos como tiempo y espacio, tradicionalmente considerados independientes, se tratan como aspectos de una sola entidad: el espacio-tiempo. Este enfoque unificado permite entender tiempo y espacio de manera distinta, de modo que puedan vincularse de formas antes impensables. Así, la idea de conmensurabilidad puede asociarse con la manera en que Einstein concibió el tiempo y el espacio, no como entidades separadas y absolutas, sino como componentes interconectados de un marco más amplio, donde la medición de uno influye en la del otro.

Y así sucesivamente.