Cantidades Directamente Proporcionales
Las cantidades directamente proporcionales son dos magnitudes relacionadas que mantienen una relación lineal constante.
Es decir, cuando una aumenta, la otra también lo hace en la misma proporción, y ocurre lo mismo si disminuye.
En matemáticas, dos magnitudes A y B son directamente proporcionales si existe una constante k tal que:
$$ A = k \cdot B $$
Esta constante k recibe el nombre de constante de proporcionalidad o razón de proporcionalidad.
$$ k = \frac{A}{B} $$
En otras palabras, existe una correspondencia uno a uno entre ambas magnitudes.
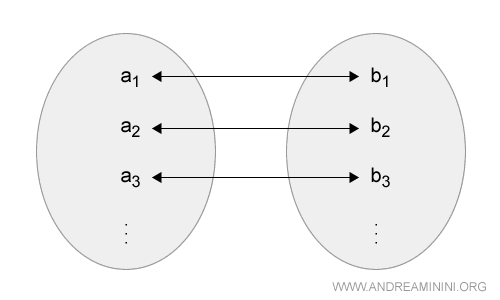
Si tomamos dos elementos cualesquiera a1 y a2 del conjunto de la magnitud A, su cociente será igual al cociente de los elementos correspondientes b1 y b2 del conjunto de la magnitud B.
$$ \frac{a_1}{a_2 }= \frac{b_1}{b_2} $$
Esto puede expresarse como: "a1 es a a2 como b1 es a b2."
$$ a_1 : a_2 = b_1 : b_2 $$
Por supuesto, esto solo es válido si a2 y b2 son distintos de cero, ya que la división por cero no está definida.
Por ejemplo, si A es directamente proporcional a B con una constante de proporcionalidad k=2, cuando B vale 3, A será 6; y cuando B vale 5, A será 10.

Supongamos que elegimos dos elementos de A, 1 y 4, cuya razón es 0,25: $$ \frac{1}{4} = 0.25 $$ Los elementos correspondientes de B son 2 y 8, y su razón también es 0,25: $$ \frac{2}{8} = 0.25 $$
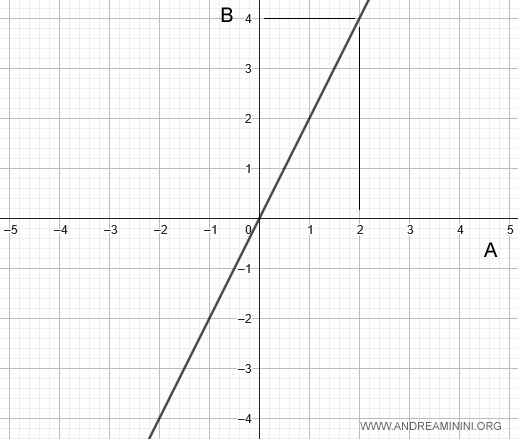
En una representación gráfica, las cantidades directamente proporcionales aparecen como una línea recta que pasa por el origen de coordenadas.
Teorema de la Proporcionalidad Directa
La condición necesaria y suficiente para que dos magnitudes homogéneas A y B sean directamente proporcionales es la siguiente:
- Si dos elementos de A son iguales, sus correspondientes en B también lo son.
- La suma de dos elementos de A corresponde exactamente a la suma de los elementos respectivos en B.
El cumplimiento de estas dos condiciones garantiza la existencia de una correspondencia uno a uno entre las magnitudes A y B.