Cantidades Inversamente Proporcionales

Dos magnitudes, A y B, son inversamente proporcionales cuando, al aumentar una, la otra disminuye de tal manera que el producto de ambas permanece constante. $$ k = A \cdot B $$

Otra forma de expresar esta relación es mediante la fórmula: A = k/B, donde k es una constante. Si B aumenta, A debe disminuir para que k se mantenga inalterada, y viceversa.

$$ A = \frac{k}{B} $$

En otras palabras, la razón entre dos elementos cualesquiera a₁ y a₂ del conjunto A es igual al recíproco de la razón entre los elementos correspondientes b₁ y b₂ del conjunto B.

$$ \frac{a_1}{a_2} = \frac{b_2}{b_1} $$

Esto también puede enunciarse como: "a₁ es a a₂ como b₂ es a b₁".

$$ a_1 : a_2 = b_2 : b_1 $$

Es fundamental que a₂ y b₁ sean distintos de cero, para evitar el problema de la división por cero.

Por ejemplo, si A es inversamente proporcional a B y su producto A·B es siempre igual a k=1, entonces cuando A vale 2, B será 0,5; y cuando A vale 4, B será 0,25. En todos los casos, el producto se mantiene constante en 1.

Otro ejemplo: tomemos dos elementos de A, 4 y 2, cuya razón es 2: $$ \frac{4}{2} = 2 $$ Los elementos correspondientes de B son 0,25 y 0,50, y su razón es el recíproco de 2, es decir, 1/2: $$ \frac{0.25}{0.5} = \frac{ \frac{1}{4} }{ \frac{1}{2} } = \frac{1}{4} \cdot \frac{2}{1} = \frac{2}{4} = \frac{1}{2} $$

En una representación gráfica, las cantidades inversamente proporcionales se describen mediante una hipérbola equilátera cuyo eje transversal coincide con la bisectriz. Esto refleja que, a medida que A aumenta y B disminuye, el producto AB permanece constante.

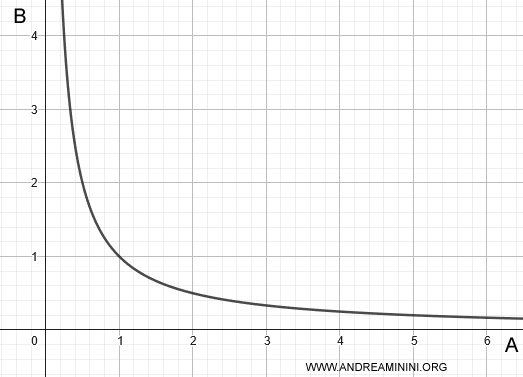
Nota: Este concepto es especialmente relevante en física. Por ejemplo, en la ley de Coulomb, la fuerza entre dos cargas eléctricas es inversamente proporcional al cuadrado de la distancia que las separa.

Un Ejemplo Práctico

Consideremos la relación entre la velocidad y el tiempo necesario para recorrer una distancia fija.

$$ \text{tiempo} = \frac{\text{distancia}}{\text{velocidad}} $$

Si la velocidad aumenta, el tiempo requerido para cubrir la distancia disminuye, pero el producto de velocidad y tiempo, que equivale a la distancia, permanece constante.

$$ \text{velocidad} \cdot \text{tiempo} = \text{distancia} $$

Por ejemplo, supongamos que deseas recorrer 100 km.

Si viajas a 50 km/h, tardarás 2 horas en completar el trayecto.

$$ \text{Tiempo} = \frac{\text{100 km}}{\text{50 km/h}} = \text{2 h} $$

Si duplicas la velocidad a 100 km/h, el tiempo necesario para recorrer la misma distancia se reduce a 1 hora.

$$ \text{Tiempo} = \frac{\text{100 km}}{\text{100 km/h}} = \text{1 h} $$

En este ejemplo, la velocidad (V) y el tiempo (T) son magnitudes inversamente proporcionales, manteniéndose constante la distancia recorrida en 100 km.

Cuando la velocidad se duplica, el tiempo se reduce a la mitad. En ambos casos, el producto de V y T es igual a 100 km.

$$ \text{50 km/h} \cdot \text{2 horas} = \text{100 km} $$

$$ \text{100 km/h} \cdot \text{1 hora} = \text{100 km} $$

Este ejemplo muestra que, manteniendo constante la distancia, un aumento en la velocidad provoca una disminución proporcional en el tiempo requerido para recorrerla.

Y así sucesivamente.