Cantidades Continuas
El postulado de continuidad de las magnitudes formaliza la idea intuitiva de que una cantidad matemática puede subdividirse en partes cada vez más pequeñas, sin que exista un límite para este proceso.
Este principio es clave para comprender la estructura de los números reales y constituye uno de los pilares sobre los que se desarrolló el análisis matemático.
Se asocia con frecuencia a Georg Cantor y a su trabajo pionero en teoría de conjuntos y en los fundamentos de la matemática moderna.
Nota: En términos más formales, el postulado de continuidad afirma que cualquier magnitud puede concebirse como un conjunto de unidades indivisibles que pueden ponerse en correspondencia biunívoca con los números enteros. Cantor empleó este principio para establecer las bases de la teoría de conjuntos y profundizar en nociones como la cardinalidad y la construcción de los números reales.
Un aspecto esencial de este postulado es la idea de magnitudes infinitamente divisibles, elemento central en el cálculo infinitesimal.
Por ejemplo, si consideramos la longitud de un segmento AB, el postulado de continuidad establece que dicho segmento puede dividirse indefinidamente en partes más y más pequeñas, sin llegar nunca a una “unidad mínima” indivisible.
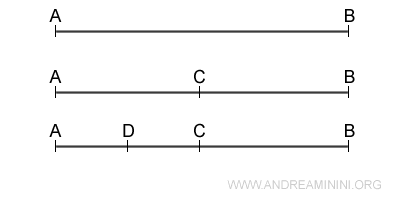
Esta posibilidad de fraccionar un segmento (o cualquier otra magnitud) sin límite alguno es lo que permite manejar con rigor conceptos como límites, derivadas e integrales.
En este sentido, el postulado de continuidad de Cantor desempeñó un papel decisivo en la formación del análisis moderno, influyendo de forma profunda en la evolución de la matemática del siglo XX.
Condujo, además, a la comprensión de que los números reales constituyen un continuo: un conjunto infinitamente divisible.
Ejemplo: Dados dos números reales distintos a<b, siempre existe un número real c tal que a<c<b. Por ejemplo, entre 2 y 3 hay infinitos números reales intermedios (2,5; 2,49; 2,77; ...). Del mismo modo, entre 2 y 2,5 también existen infinitos números intermedios. Y así hasta el infinito.
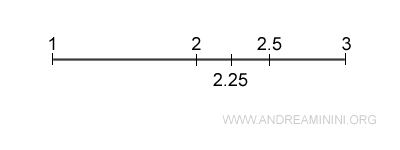
Este hecho es fundamental para entender la densidad de los números reales y, en general, de cualquier conjunto numérico denso.
Esta concepción ha permitido resolver paradojas y problemas relacionados con el infinito y la continuidad en las funciones matemáticas.
Un ejemplo clásico es la paradoja de Zenón, que pone de manifiesto las dificultades a las que se enfrentaron los matemáticos griegos para conceptualizar el infinito y la división indefinida.
Zenón sostenía que una liebre (o Aquiles) nunca podría alcanzar a una tortuga si esta tuviera ventaja inicial, ya que la liebre debería primero llegar al punto de partida de la tortuga, momento en el que esta ya se habría adelantado más.
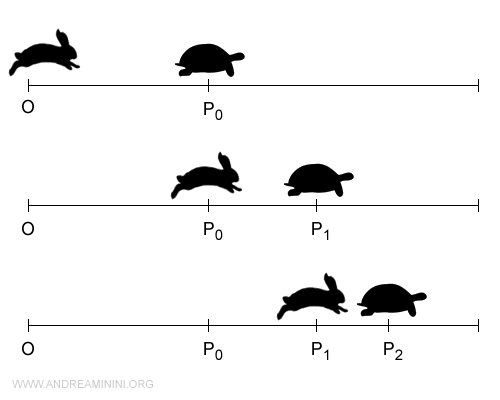
El postulado de continuidad tuvo también profundas repercusiones en el desarrollo del cálculo infinitesimal.
Las nociones mismas de límite y continuidad se basan en la idea de que es posible aproximarse a un valor tanto como se quiera, sin necesidad de alcanzarlo exactamente.
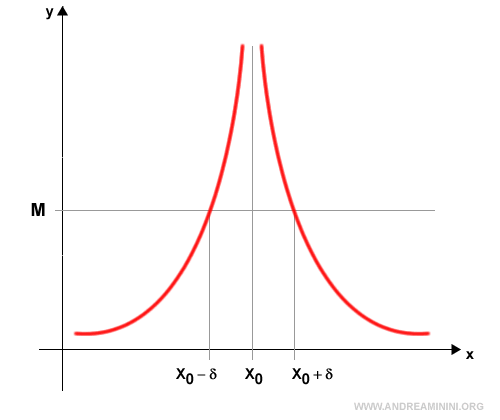
Este concepto es particularmente importante en el cálculo de derivadas e integrales, donde se opera con magnitudes infinitesimales.
Y así sucesivamente.